海南大学：《结构力学》课程教学资源（PPT课件）第十一章 矩阵位移法

结构力学一—第十一章矩阵位移法 海南大学土木建筑工程学院 将式（115)写成矩阵形式，即可得单元坐标 系中一般单元的单元刚度方程 EA EA 0 0 0 0 (e) 12E1 6EI 12E1 6EI 0 0 e 12 1 P 6EI 4EI -6EI 2EI 0 0 EA EA 0 0 0 0 4040 -12E1 -6E1 12E1 6E1 0 0 P 6E1 2EI -6E1 4EI 0 2 (11-6) 27

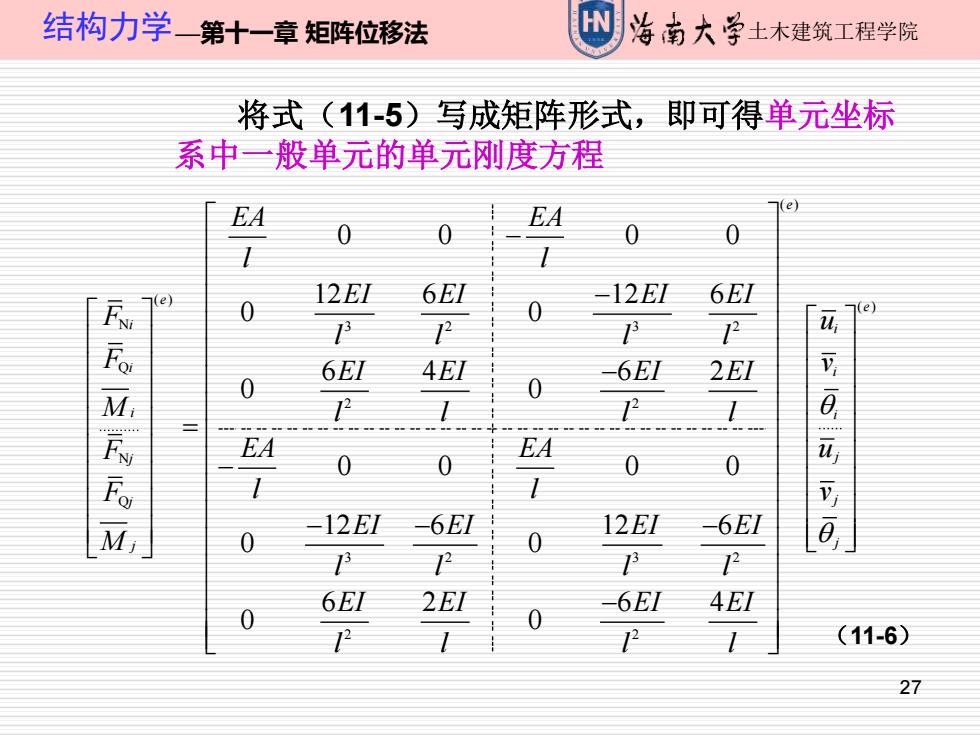
27 结构力学—第十一章 矩阵位移法 土木建筑工程学院 将式（11-5）写成矩阵形式，即可得单元坐标 系中一般单元的单元刚度方程 ( ) ( ) N 3 2 3 2 Q 2 2 N Q 3 2 3 2 2 2 0 0 0 0 12 6 12 6 0 0 6 4 6 2 0 0 0 0 0 0 12 6 12 6 0 0 6 2 6 4 0 0 e e i i i i i j j j EA EA l l EI EI EI EI F u l l l l F v EI EI EI EI M l l l l F EA EA F l l EI EI EI EI M l l l l EI EI EI EI l l l l q   −   −       −     =   −       − − −   −   ( ) e i j j j u v q                     （11-6）

结构力学一—第十一章矩阵位移法 海南大学土木建筑工程学院 上式也可简写为 Fe=δ9 (11-7) 其中 EA (e) 0 0 EA 0 0 1 12E1 6EI 12E/ 6EI 0 0 P 1 6EI 4EI 6E1 2El 0 0 K= (11-8) EA 0 EA 0 0 0 1 -6E1 12EI 0 -12E1 0 -6E1 /3 3 12 6EI 2E1 -6EI 4EI 0 12 28

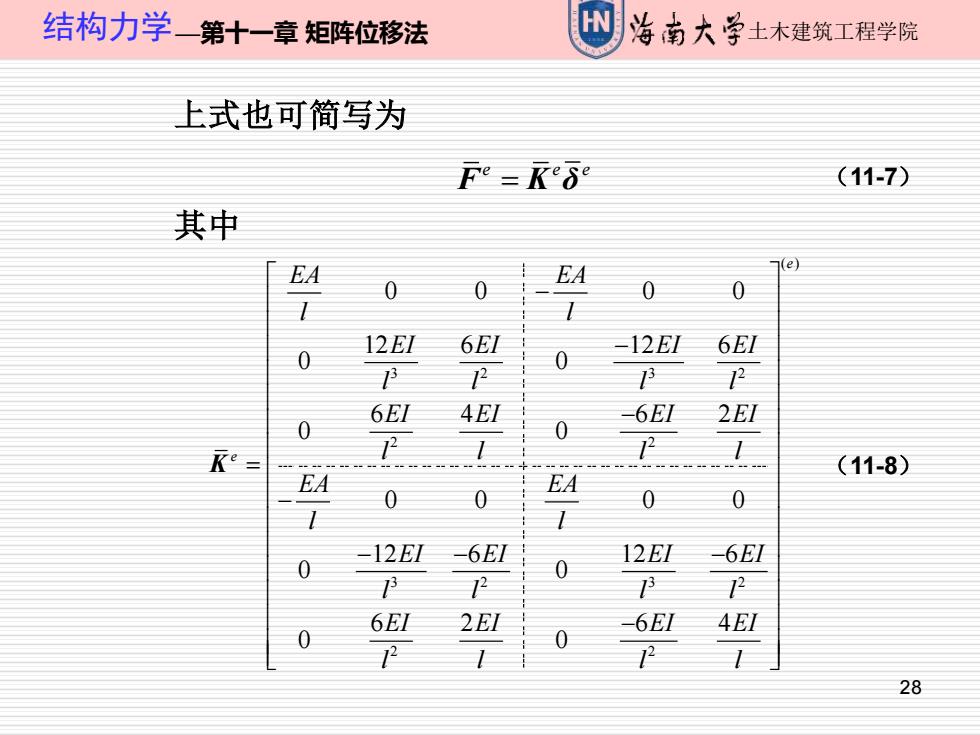
28 结构力学—第十一章 矩阵位移法 土木建筑工程学院 上式也可简写为 其中 e e e F K= δ （11-7） ( ) 3 2 3 2 2 2 3 2 3 2 2 2 0 0 0 0 12 6 12 6 0 0 6 4 6 2 0 0 0 0 0 0 12 6 12 6 0 0 6 2 6 4 0 0 e e EA EA l l EI EI EI EI l l l l EI EI EI EI l l l l EA EA l l EI EI EI EI l l l l EI EI EI EI l l l l   −   − − = − − − − −   K （11-8）

结构力学一第十一章矩阵位移法 W 洛南大学土木建筑工程学院 称为一般单元的单元刚度矩阵，简称单刚。 矩阵位移法仅采用位移法中的两端固支单跨超 静定梁来推导单元刚度方程，这使得其基本单元类 型归一化，更便于应用程序的开发。 11.3.2特殊单元 杆端独立位移未知量因被约束变为已知位移， 或者不独立于其它杆端位移的单元，称为特殊单元。 例如连续梁单元和理想桁架单元等。 (1)连续梁单元 忽略轴向变形的连续梁或无结点线位移的刚架， 经过离散化后，单元两端只有独立的杆端转角未知 量和0.0 29

29 结构力学—第十一章 矩阵位移法 土木建筑工程学院 称为一般单元的单元刚度矩阵，简称单刚。 矩阵位移法仅采用位移法中的两端固支单跨超 静定梁来推导单元刚度方程，这使得其基本单元类 型归一化，更便于应用程序的开发。 11.3.2 特殊单元 杆端独立位移未知量因被约束变为已知位移， 或者不独立于其它杆端位移的单元，称为特殊单元。 例如连续梁单元和理想桁架单元等。 （1）连续梁单元 忽略轴向变形的连续梁或无结点线位移的刚架， 经过离散化后，单元两端只有独立的杆端转角未知 量 和 。 e K q i q j

结构力学一—第十一章矩阵位移法 海南大学土木建筑工程学院 将线位移u=,=u,=亚，=0的条件代入式（11 6)中，并注意到杆端剪力不独立于杆端弯矩，则 可得连续梁单元的单元刚度方程为 4E1 2E1 e M (e) (11-9) 2E1 4E1 相应的单元刚度矩阵为 4E1 2EI (e) = (11-10) 2EI 4EI 30

30 结构力学—第十一章 矩阵位移法 土木建筑工程学院 将线位移 的条件代入式（11- 6）中，并注意到杆端剪力不独立于杆端弯矩，则 可得连续梁单元的单元刚度方程为 u v u v i i j j = = = = 0 ( ) ( ) ( ) 4 2 2 4 e e e i i j j EI EI M l l M EI EI l l q q           =                 （11-9） 相应的单元刚度矩阵为 ( ) 4 2 2 4 e EI EI l l EI EI l l     =         e K （11-10）

结构力学一第十一章矩阵位移法 洛南大学士木建筑工程学院 可见，连续梁单元的单刚可以由一般单元单刚 划去与零位移相应的行和列，即式(11-8)中的第 1、2、4、5行和列而得。 (2)理想桁架单元 理想桁架中的各杆件只有轴向变形，即u≠0， u≠0。而=亚=0=0=0，将这一条件代入式 (11-6),可得理想桁架单元的单元刚度方程为 EA EA (e) (e) (11-11) EA EA 相应的单元刚度矩阵为 31

31 结构力学—第十一章 矩阵位移法 土木建筑工程学院 可见，连续梁单元的单刚可以由一般单元单刚 划去与零位移相应的行和列，即式（11-8）中的第 1、2、4、5行和列而得。 （2）理想桁架单元 理想桁架中的各杆件只有轴向变形，即 ， 。而 ，将这一条件代入式 （11-6），可得理想桁架单元的单元刚度方程为 0 i u  uj  0 v v i j i j = = = = q q 0 ( ) ( ) ( ) N N e e e i i j j EA EA F l l u F EA EA u l l   −         =           −     （11-11） 相应的单元刚度矩阵为