上海交通大学：《概率论与数理统计》课程教学资源（课件讲稿）09、多维随机变量及分布 §3.5 二维随机变量函数的分布

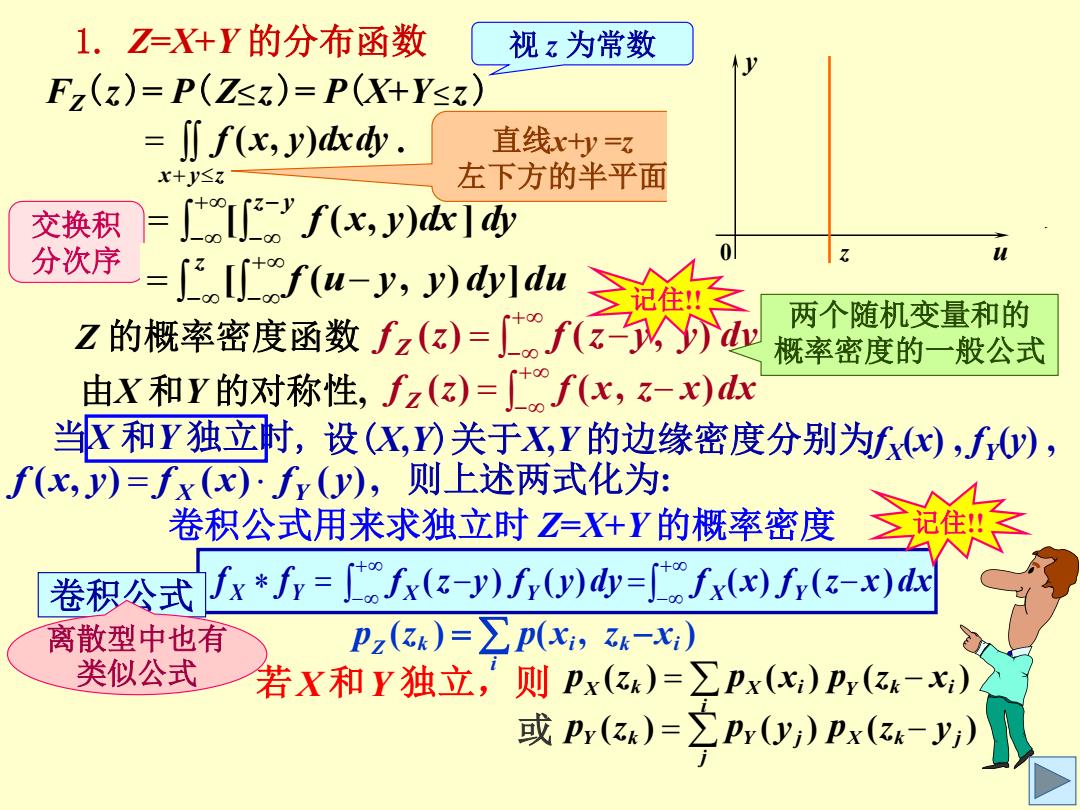
1.Z=X+Y的分布函数 视z为常数 F,（z)=P(Zsz)=PX+Y≤z) =∬f(x,y)dky. 直线x+y=乙 x+y≤z 左下方的半平面 交换积 =f'f(x,y)] 分次序 =fu-八，)d三条 Z的概率密度函数fz(z)=f(z个)dm 两个随机变量和的 概率密度的一般公式 由X和Y的对称性，fz(z)=f(x,z-x)x 当驱和Y独立时，设(X,)关于X,Y的边缘密度分别为fx),fy), f(x,y)=fx(x)f(y),则上述两式化为： 卷积公式用来求独立时Z=X+Y的概率密度 卷积公式∫x*乐=」fx(亿-y)f0)d=∫fx(x)f(a-x)瓜 离散型中也有 Pz(zk)=∑p(x,k-x) 类似公式 若X和Y独立，则Px(z)=∑Px(x Py(Zk-xi) 或P(x)=2P,)Px(-)

当X 和Y 独立时, 令x=u–y ( , ) .     x y z f x y dxdy 1. Z=X+Y 的分布函数 FZ(z)= P(Z≤z)= P(X+Y≤ z )         f x y dx dy z y [ ( , ) ] x+y  z    z y f (x, y)dx 0 X Y    z f (u y, y)du   z f (u y, y)du f z f z y f y dy f x f z x dx Z  X Y  X Y       ( )  (  ) ( )  ( ) (  ) 直线x+y =z 左下方的半平面 设(X,Y)关于X,Y 的边缘密度分别为fX (x) , fY (y) , f (x, y) f (x) f ( y), 则上述两式化为: X Y   卷积公式用来求独立时 Z=X+Y 的概率密度 x+y = z 0 z u y 由概率密度与分布函数的关系: F(x) f (t)dt , F (x) f (x) x      Z 的概率密度函数 f z f z y y dy Z     ( )  (  , ) f Z z  f x z x dx    由X 和Y 的对称性, ( )  ( ,  ) 两个随机变量和的 概率密度的一般公式 卷积公式 f X  f Y  离散型中也有 类似公式 记住!! 记住!! [ ]dy      交换积 分次序 视 z 为常数    i pZ (zk ) p(xi , zk xi ) 若X 和Y 独立，则    i pX (zk ) pX (xi ) pY (zk xi )    j 或 pY (zk ) pY ( yj ) pX (zk yj ) f u y y dy du z [ ( , ) ]       

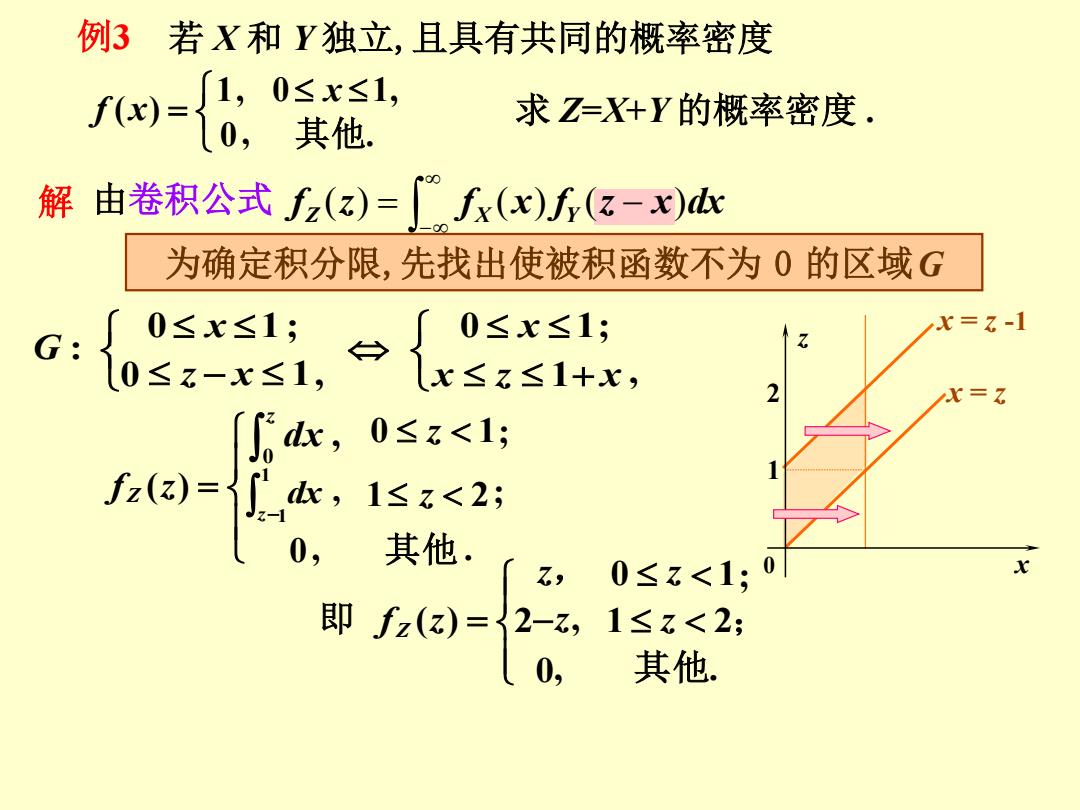
例3 若X和Y独立，且具有共同的概率密度 w= 求Z=X+Y的概率密度. 其他. 解由卷积公式fz(z)=fx(x)f(z-r) 为确定积分限，先找出使被积函数不为0的区域G G: 0≤x≤1； 0≤x≤1； X=z-1 0≤z-x≤1， x≤z≤1+x, 2 x=Z [6c,0≤z<l; fz(3)=d,1≤z<2; 0,其他. z,0≤z<1:0 x 即fz()={2-z, 1≤z<2; 0, 其他

        0 1; ( ) z f Z z 为确定积分限,先找出使被积函数不为 0 的区域G 若 X 和 Y 独立,且具有共同的概率密度 求 Z=X+Y 的概率密度 .       0, . 1, 0 1, ( ) 其他 x f x    由卷积公式 f Z (z)  f X (x) f Y (z  x)dx         0 1, 0 1 ; : z x x G          1 , 0 1; x z x x 例3 解  z dx 0 , x = z -1 2 x = z 1 0 x z 1 z  2; 0, 其他 .   1 1 , z dx           0, . 2 , 1 2 0 1; ( ) 其他 ； ， 即 z z z z fZ z

例4(P.89例5)若X和Y相互独立，且均服从N(0,1),求Z=X+Y的密度. 解fx(x)=D 2, -0<X<+00; 2π f0)=2ze,-<y<+o 由卷积公式 f,f,k-=2eek元 d 2元J- 均匀分布？ e=2元e.Z服从正态分布N0,2. 类似地可以证明： 若X和Y独立，且X~N(4,o),Y~N(42,o), 泊松分布、·二项分布 也有相应结论 → Z=X+Y~N(41+42,o1+o) 此结论推广到个独立的正态随机变量之和的情形请自行写出结论 更一般地，可以证明：若X;~N(4,O),且X1,X2,…,Xn独立，则 2aX,~N(244,2听o), 其中，(i=1,2,…,n)为常数. 服从正态分布的有限个独立随机变量的线性组合仍服从正态分布 如设X,Y独立，都具有正态分布，则3X+4Y+1也具有正态分布

如设X,Y 独立,都具有正态分布，则 3X+4Y+1也具有正态分布 类似地可以证明: ~ ( , ) 2 2 2  Z  X Y N 1   2  1  若X和Y 独立, 此结论推广到 n个独立的正态随机变量之和的情形 例4(P.89例5) 若X和Y相互独立,且均服从N(0,1), 求Z=X+Y 的密度. 解 f x  e   x ； x X , 2 1 ( ) 2 2  f y  e   y ， y Y , 2 1 ( ) 2 2  由卷积公式    f z  f x f z  x dx Z X Y ( ) ( ) ( ) e e dx x z x        2 2 2 ( ) 2 2 1  e e dx z x z        2 2 ) 2 ( 4 2 1  令 2 z t  x e e dt t z       2 2 4 2 1  . 2 1 4 2 z e    ~ ( , ), ~ ( , ), 2 2 2 2 且 X N  1  1 Y N   请自行写出结论 服从正态分布的有限个独立随机变量的线性组合仍服从正态分布 更一般地, 可以证明: 泊松分布、二项分布 也有相应结论 均匀分布? 其中ai ( i =1,2,…, n)为常数. ~ ( , ), 1 2 2 1 1       n i i i n i i i n i aiXi N a  a  ~ ( , ), 2 i i 若 Xi N   且 X1 , X2 , …, Xn 独立, 则 ∴ Z 服从正态分布N(0,2)