
例 6.2.1最大均匀抽取滤波器组 给定低通原型:H) h(n) 靠移位生成 H()=Ho(WR) H,(eo)=H(eo-2*) 2 则: H(E),H(a)5…,H-(a) 均匀抽取滤波器组 如果每个子带再M倍抽取,且 M=K→ 最大均匀抽取滤波器组
6.2.1 最大均匀抽取滤波器组 给定低通原型: 靠移位生成 均匀抽取滤波器组 最大均匀抽取滤波器组 ( ) ( ) 0 k k K H z H zW ( ) ( ) ( 2 / ) 0 j j k K k H e H e ( ) 0 H z h (n) k ( ), ( ), , ( ) 0 1 1 H z H z H z k M K 则: 如果每个子带再M倍抽取,且
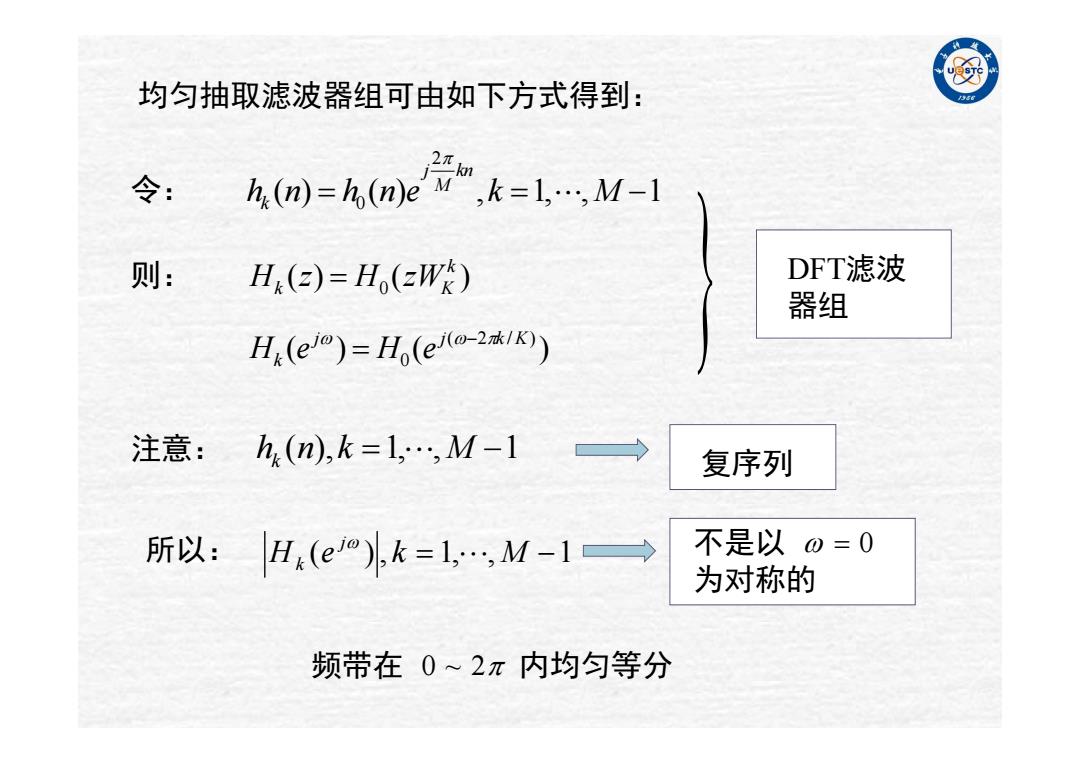
例 均匀抽取滤波器组可由如下方式得到: 2π 令: h(n)=ho(n)e Mk=1,..,M-1 则: H()=Ho(zWR) DFT滤波 器组 Hx(e)=H,(ea-21) 注意:h(n),k=1,…,M-1 复序列 所以:H(eo),k=1,,M-1→ 不是以0=0 为对称的 频带在0~2π内均匀等分
均匀抽取滤波器组可由如下方式得到: 2 0 ( ) ( ) , 1, , 1 j kn M k h n h ne k M ( ) ( ) 0 k k K H z H zW ( ) ( ) ( 2 / ) 0 j j k K k H e H e h ( n), k 1,,M 1 k H ( e ), k 1,, M 1 j k 0 ~ 2 0 令: 则: 注意: 所以: 频带在 内均匀等分 DFT滤波 器组 复序列 不是以 为对称的
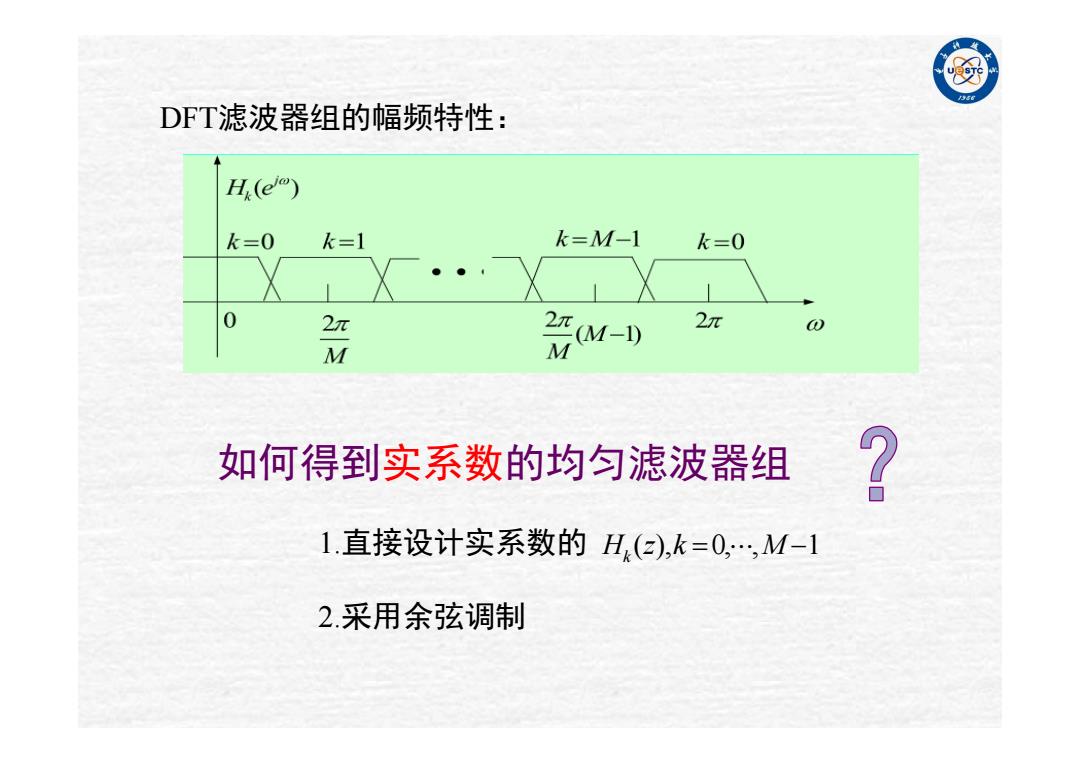
例 DFT滤波器组的幅频特性: H(e) k=0 k=1 k=M-1 k=0 0 2π 2π M (- 如何得到实系数的均匀滤波器组 ? 1.直接设计实系数的H(z),k=0,·,M-1 2.采用余弦调制
DFT滤波器组的幅频特性: 如何得到实系数的均匀滤波器组 1.直接设计实系数的 2.采用余弦调制 H (z),k 0,,M 1 k
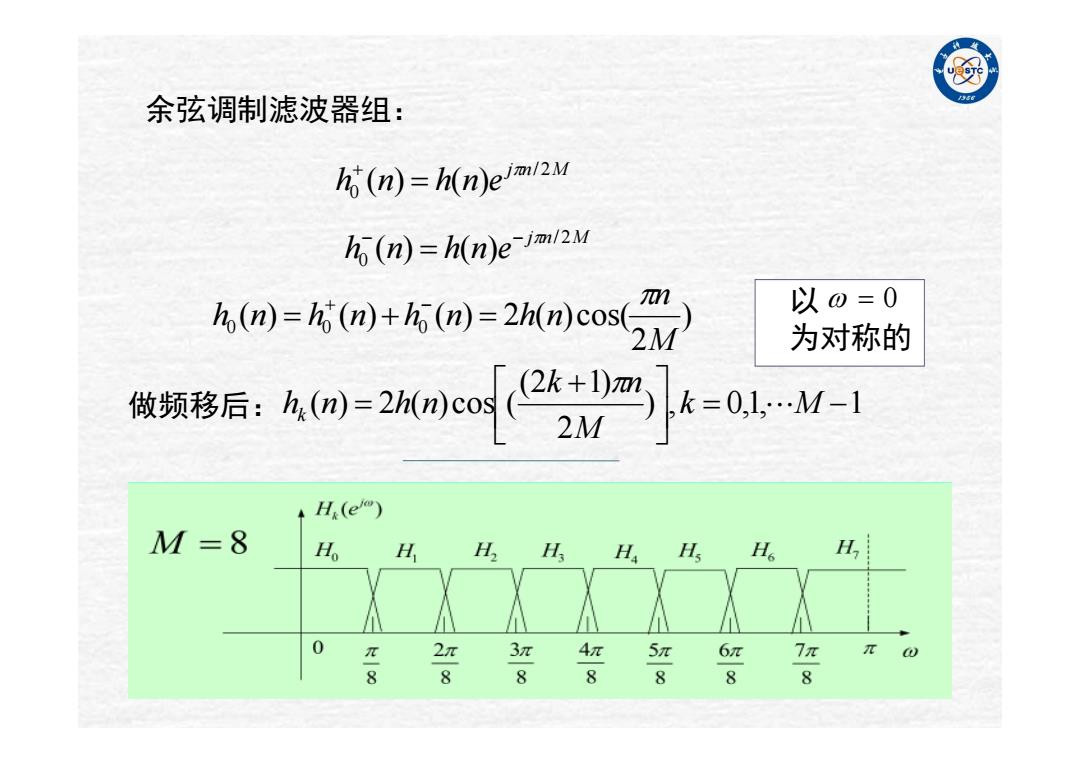
例 余弦调制滤波器组: h时(n)=h(n)eo2M h(n)=h(n)e-im2M h (n)=(n)(n)=2h(n)cos( 以0=0 为对称的 ®项移后:A=2acm2W4=0l- H(e) M=8 H HH.HHHH 、H, 0 π 8
余弦调制滤波器组: j n M h n h n e / 2 0 ( ) ( ) j n M h n h n e / 2 0 ( ) ( ) ) 2 ( ) ( ) ( ) 2 ( )cos( 0 0 0 Mn h n h n h n h n ) , 0,1, 1 2 (2 1) ( ) 2 ( )cos ( k M Mk n h n h n k 做频移后: 以 0 为对称的

6.2.2正交镜像滤波组 (Quadrature Mirror Filter Bank,QMFB) 考虑两通道滤波组 H,(e') ol- 2 H(e)=0, 2 Hi(e)=H(e-)
6.2.2 正交镜像滤波组 (Quadrature Mirror Filter Bank,QMFB) 考虑两通道滤波组 ( ) 0 j H e 0 3 ( ) 0, 2 2 j H e ( ) ( ) ( ) 1 0 j j H e H e 2