
1 2

固定端(插入端)约束 说明 ①认为F这群力在同一 平面内; ②将F向A点简化得一 力和一力偶; RA M ③R方向不定可用正交 分力Y,X表示; ④ Y,X,M4为固定端 M 约束反力; A ⑤Y,X限制物体平动, M为限制转动
固定端(插入端)约束 说明 ①认为Fi这群力在同一 平面内; ② 将Fi向A点简化得一 力和一力偶; ③RA方向不定可用正交 分力YA, XA表示; ④ YA , XA , MA为固定端 约束反力; ⑤ YA, XA限制物体平动, MA为限制转动
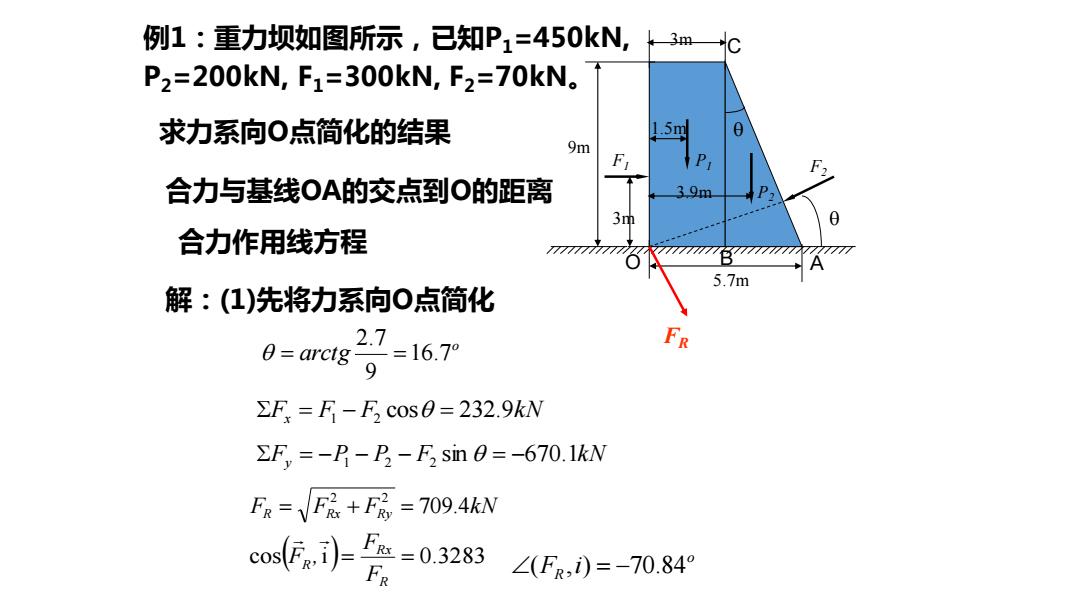
例1:重力坝如图所示,已知P1=450kN,k3mc P2=200kN,F1=300kN,F2=70kN。 求力系向O点简化的结果 1.5m 9m F F 合力与基线OA的交点到O的距离 39m 3印 0 合力作用线方程 777777777 7777 A 5.7m 解:(1)先将力系向O点简化 0=arctg- 2.7=1679 FR ∑F=F-F,cos0=232.9kW EF=-P-P-F2 sin 0=-670.1kN FR=VF+F路=709.4kW cos))=5=0.3283 ∠(FR,i)=-70.84°
例1:重力坝如图所示,已知P1=450kN, P2=200kN, F1=300kN, F2=70kN。 求力系向O点简化的结果 合力与基线OA的交点到O的距离 合力作用线方程 解:(1)先将力系向O点简化 F1 F2 P1 P2 5.7m 9m 3m 3.9m 1.5m 3m O A B C o arctg 16.7 9 2.7 = = Fx = F1 − F2 cos = 232.9k N Fy = −P1 − P2 − F2 sin = −670.1k N FR FRx FRy 709.4k N 2 2 = + = cos( i)= = 0.3283 R Rx R F F F , o R (F ,i) = −70.84 FR
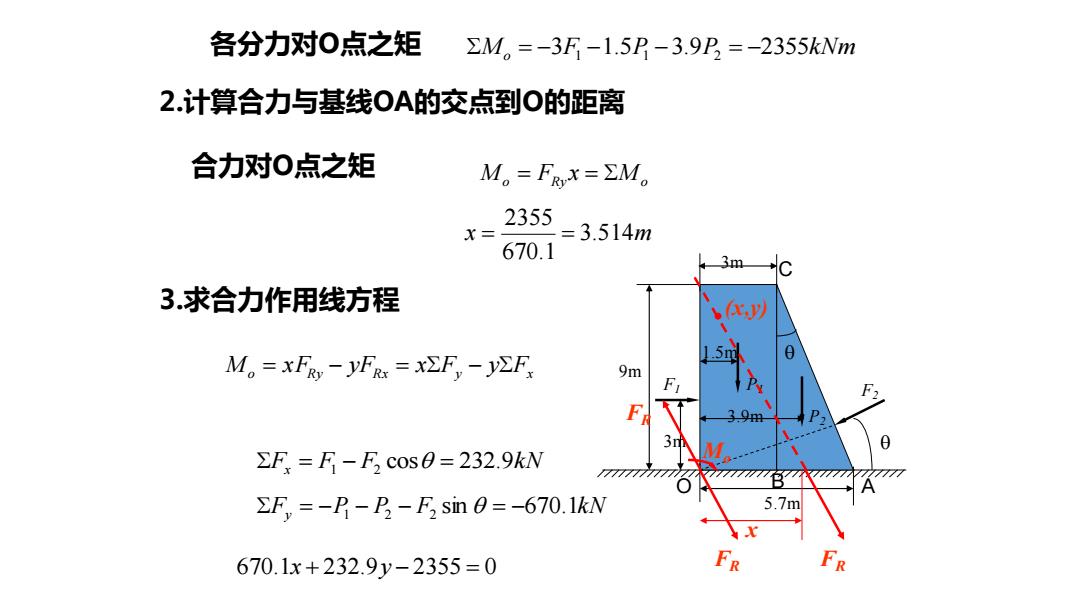
各分力对0点之矩 ∑M=-3F-1.5P-3.9P,=-2355kNm 2.计算合力与基线0A的交点到O的距离 合力对0点之矩 M。=FRx=∑M 2355 x= 670.1 =3.514m 43m C 3.求合力作用线方程 A以 M。=xFR-yFR=xEF,-yEF 9m F2 3.9m 3 ∑F=F-Fcos0=232.9kW 777777 77777 ∑F,=--P-F3sin0=-670.1kW 5.7m 670.1x+232.9y-2355=0
Mo = −3F1 −1.5P1 −3.9P2 = −2355kNm 2.计算合力与基线OA的交点到O的距离 各分力对O点之矩 合力对O点之矩 o Ry Mo M = F x = x 3.514m 670.1 2355 = = 3.求合力作用线方程 o Ry Rx y Fx M = x F − yF = xF − y 670.1x + 232.9y − 2355 = 0 F1 F2 P1 P2 5.7m 9m 3m 3.9m 1.5m 3m O A B C FR Mo FR FR x (x,y) Fx = F1 − F2 cos = 232.9k N Fy = −P1 − P2 − F2 sin = −670.1k N

§2一4平面任意力系的平衡条件和平衡方程 平面力系的平衡的充要条件是: 力系的主矢和对任意点的主矩均等于零: FR=∑F,i+∑Fj=0 M=∑M(E)=0
平面力系的平衡的充要条件是: 力系的主矢和对任意点的主矩均等于零: i j FR = Fxi + Fyi ( ) M Mo Fi = = 0 = 0 F1 F2 F3 §2-4 平面任意力系的平衡条件和平衡方程