001 010 0 0 10 01 1 0 011 100 0 1 0 0 000 1 (4)选择触发器。本例选用功能比较灵活的JK触发器 (5)求各触发器的驱动方程和进位输出方程。 列出JK触发器的驱动表如表5-6所示。画出电路的次态卡诺图如图5-15所示 三个无效状态101、110、111作无关项处理。根据次态卡诺图和JK触发器的驱动表 可得各触发器的驱动卡诺图如图5-16所示。 表5-6JK触发晷的驱动表 g→g J %00011110 0 0 0 X 路o001010100011 0 1 1000××× 0 1 图515次态卡诺图 1 ⑤6m01110 ①400m110 6.0冈× ⑥401110 吟,xx卫 ××xx 10x×× 0××× 喝 =哈 6=暖 区冈 。×区▣0 ⑥4m410 区可 11××8 ×x× 1儿x××x =1 名=% =1 图5-16各触发器的驱动卡诺图 再画出输出卡诺图如图5-17所示,可得电路的输出(② 方程:Z= (5-12 g 00 01 11 0 0000 将各驱动方程与输出方程归纳如下: J。=g2 K。=1 (5-13a) 1×× z-g 图5-17输出卡诺图
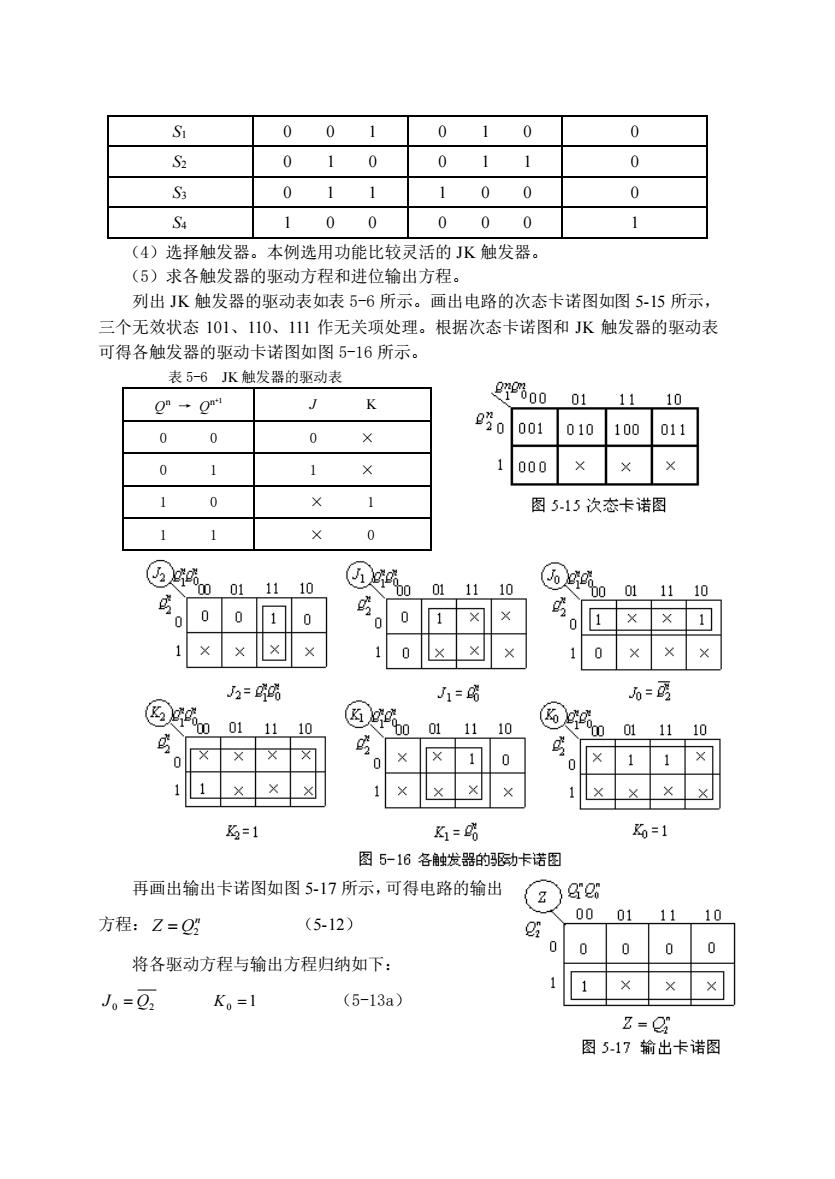
S1 0 0 1 0 1 0 0 S2 0 1 0 0 1 1 0 S3 0 1 1 1 0 0 0 S4 1 0 0 0 0 0 1 (4)选择触发器。本例选用功能比较灵活的 JK 触发器。 (5)求各触发器的驱动方程和进位输出方程。 列出 JK 触发器的驱动表如表 5-6 所示。画出电路的次态卡诺图如图 5-15 所示, 三个无效状态 101、110、111 作无关项处理。根据次态卡诺图和 JK 触发器的驱动表 可得各触发器的驱动卡诺图如图 5-16 所示。 表 5-6 JK 触发器的驱动表 Q n → Q n+1 J K 0 0 0 × 0 1 1 × 1 0 × 1 1 1 × 0 再画出输出卡诺图如图 5-17 所示,可得电路的输出 方程: 2 n Z Q= (5-12) 将各驱动方程与输出方程归纳如下: 0 Q2 J = K0 =1 (5-13a)
J1=Q。K,=Q (5-136) J2=QQ1K2=1 (5-13c】 Z=0 (5-14) (6)画逻辑图。根据驱动方程和输出方程,画出5进制计数器的逻辑图如图5-18 所示。 图518【例5-4】逻辑图 (7)检查能否自启动。利用逻辑分析的方法画出电路完整的状态图如图5-19所示。 可见,如果电路进入无效状态101、110、111时在CP脉冲作用下,分别进入有效状 态010、010、000。所以电路能够自启动。 ( 110 (101 /1 串行 00(0010 数据 检测 器 0/ (100)011 图5-20串行数据检测器框图 图519完整的状态图 【例5-5】设计一个串行数据检测器,要求是:连续输入三个或三个以上的1时输出 为1,否则输出为0。 解:(1)逻辑抽象。首先需要确定串行数据检测器的输入和输出信号。串行数据检测 器应该具有一个串行数据输入端,用X表示:具有一个输出信号Z用来表示检测结果, 即串行数据检测器的框图如图5-20所示。 根据设计要求,检测器在以下输入信号X的作用下,其输出信号Z的输出应为 X:0101101110111101 Z:0000000010001100 由于电路用于检测“111”序列,所以需要识别输入1的个数,故预设电路具有S、 S、S和S,四个状态。S,表示电路当前没有接收到一个1,S,表示电路当前已经接收
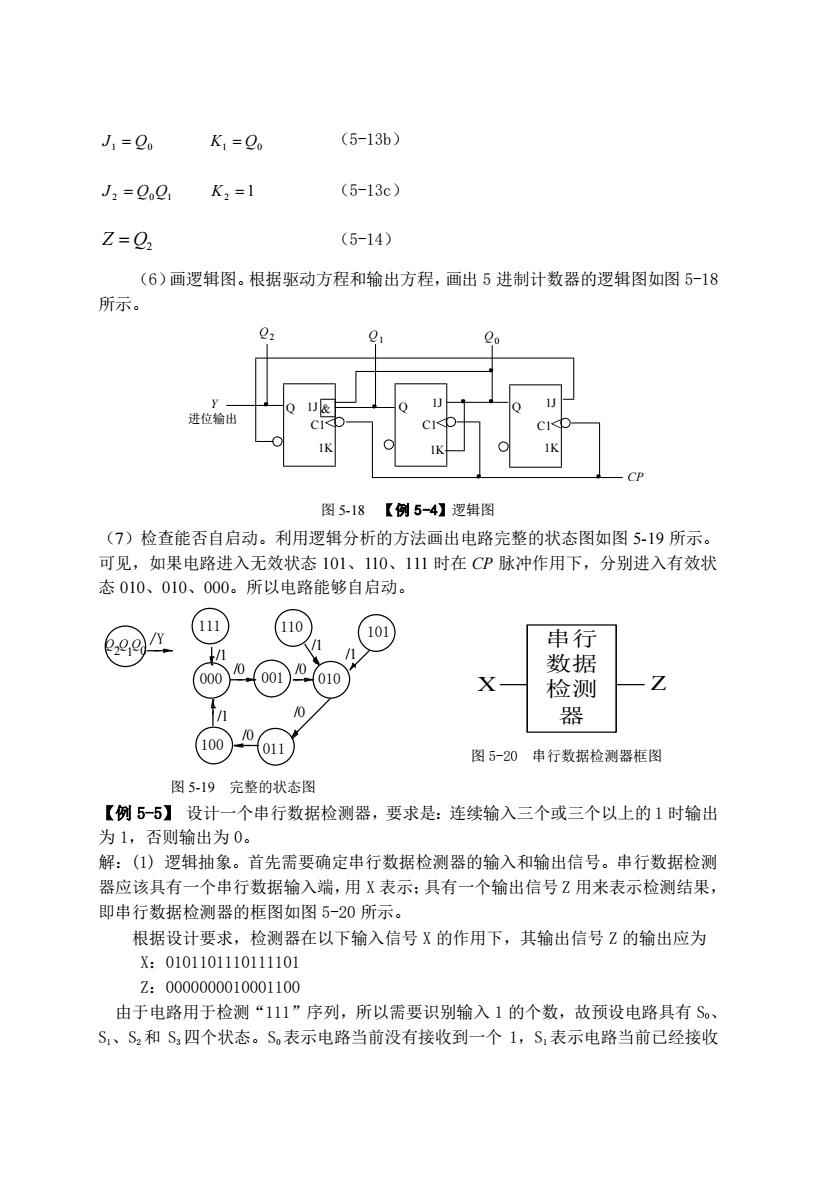
1 Q0 J = K1 = Q0 (5-13b) 2 Q0Q1 J = K2 =1 (5-13c) Z Q= 2 (5-14) (6)画逻辑图。根据驱动方程和输出方程,画出 5 进制计数器的逻辑图如图 5-18 所示。 Q C1 C1 Q 1K 1J ∧ 1J 1J ∧ 1K 1K C1 Q ∧ & 2 Q0 Q Q1 CP Y 进位输出 图 5-18 【例 5-4】逻辑图 (7)检查能否自启动。利用逻辑分析的方法画出电路完整的状态图如图 5-19 所示。 可见,如果电路进入无效状态 101、110、111 时在 CP 脉冲作用下,分别进入有效状 态 010、010、000。所以电路能够自启动。 图 5-19 完整的状态图 【例 5-5】 设计一个串行数据检测器,要求是:连续输入三个或三个以上的 1 时输出 为 1,否则输出为 0。 解:(1) 逻辑抽象。首先需要确定串行数据检测器的输入和输出信号。串行数据检测 器应该具有一个串行数据输入端,用 X 表示;具有一个输出信号 Z 用来表示检测结果, 即串行数据检测器的框图如图 5-20 所示。 根据设计要求,检测器在以下输入信号 X 的作用下,其输出信号 Z 的输出应为 X:0101101110111101 Z:0000000010001100 由于电路用于检测“111”序列,所以需要识别输入 1 的个数,故预设电路具有 S0、 S1、S2 和 S3 四个状态。S0 表示电路当前没有接收到一个 1,S1 表示电路当前已经接收 0 Q Q 1 Q 2 /Y 000 001 010 011 100 /0 /0 /0 /0 /1 /1 101 /1 111 110 /1 串行 数据 检测 器 X Z 图 5-20 串行数据检测器框图
到一个1,S2表示电路当前己经接收到两个1,S,表示电路当前己经接收到三个1。在 输入信号X的作用下,电路的状态转换关系和输出如图521所示。 X/Y )11 0/0 0/0 0/0 所示状态转换表。 表5-7串行检测器的状态转换表 X 0 。 So/0 S/0 S So/0 S20 S/0 S3/0 S: So/0 S:/0 从表中可以看出,S和S,两个状态在相同的输入条件下具有相同的输出,并且转 换到相同的次态中去,故S,和S为等价状态,可以合并成一个,如表5-8所示。这从 概念上也不难理解,当电路处于S2时表示己经接收到两个1,如果电路在转换到S 的同时输入也切换到下一个输入数据,那么只要下一个数据为1,就表明已经连续输 入三个1了,因而不需要再设一个状态 表5-8化简后的状态转换表 0 So So/0 S1/0 S So/0 S2/0 S2 So/0 S3/0 (3)选用触发器的类型和个数。因电路为3个状态,应取2个触发器,状态分别 用Q1、Q0表示。本例选用D型触发器。 (④状态编码。串行数据检测器对内部状态的编码没有特殊的要求,故选取00、 01、10分别编码S、S1和S2。 (⑤)求电路的状态方程,驱动方程和输出方程。根据表5-6所示的状态表可画出 触发器次态QQ和输出Z的卡诺图如图5-22所示
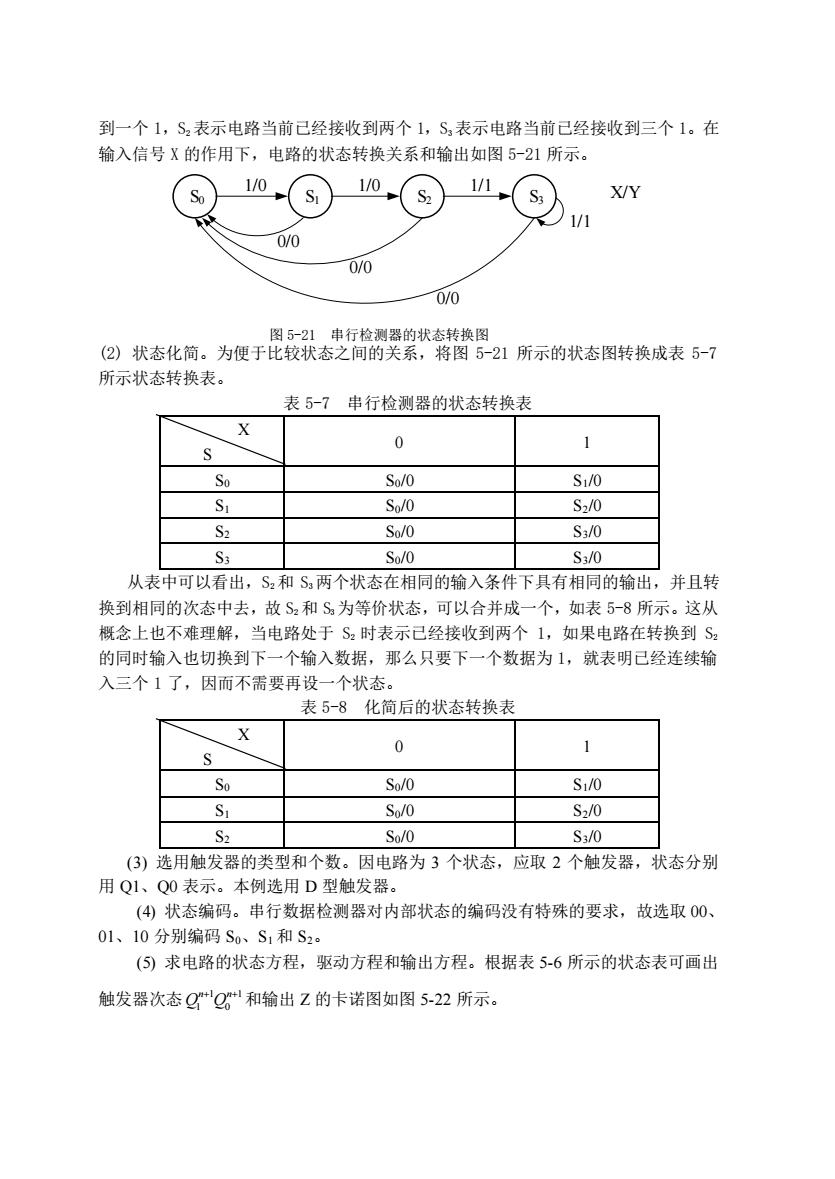
到一个 1,S2 表示电路当前已经接收到两个 1,S3 表示电路当前已经接收到三个 1。在 输入信号 X 的作用下,电路的状态转换关系和输出如图 5-21 所示。 S3 1/0 1/0 1/1 S0 S1 S2 X/Y 0/0 0/0 0/0 1/1 (2) 状态化简。为便于比较状态之间的关系,将图 5-21 所示的状态图转换成表 5-7 所示状态转换表。 表 5-7 串行检测器的状态转换表 X S 0 1 S0 S0/0 S1/0 S1 S0/0 S2/0 S2 S0/0 S3/0 S3 S0/0 S3/0 从表中可以看出,S2 和 S3 两个状态在相同的输入条件下具有相同的输出,并且转 换到相同的次态中去,故 S2 和 S3 为等价状态,可以合并成一个,如表 5-8 所示。这从 概念上也不难理解,当电路处于 S2 时表示已经接收到两个 1,如果电路在转换到 S2 的同时输入也切换到下一个输入数据,那么只要下一个数据为 1,就表明已经连续输 入三个 1 了,因而不需要再设一个状态。 表 5-8 化简后的状态转换表 X S 0 1 S0 S0/0 S1/0 S1 S0/0 S2/0 S2 S0/0 S3/0 (3) 选用触发器的类型和个数。因电路为 3 个状态,应取 2 个触发器,状态分别 用 Q1、Q0 表示。本例选用 D 型触发器。 (4) 状态编码。串行数据检测器对内部状态的编码没有特殊的要求,故选取 00、 01、10 分别编码 S0、S1 和 S2。 (5) 求电路的状态方程,驱动方程和输出方程。根据表 5-6 所示的状态表可画出 触发器次态 1 1 1 0 n n Q Q+ + 和输出 Z 的卡诺图如图 5-22 所示。 图 5-21 串行检测器的状态转换图
QQ 00 01 11 0 00/0 00/0 XX/X 00/0 1 01/0 10/0 XX/X 10/1 图5-22g/的卡诺图 将图5-22的卡诺图分解为图5-23所示的三个卡诺图,分别表示、和输 出Z三个逻辑函数。 000111 10 0001 11 10 0111 10 000x0 0 0 0x0 0x0 0 0X) (a)Q 图5-23卡诺图的分解 经化简后得到触发器的状态方程为 [o"xa+xa xaa (5-15) lo"xag 与D触发器的特性方程相比较,可得串行数据检测器的驱动方程为 ID=xao (5-16) D=xoo 输出方程为Z=XQ (5-17) (6)自启动功能检查。 将无效状态11代入状态方程得到次态为10,故设计的电路具有自启动功能。 (7)根据式(5-16)的驱动方程和式(5-17)的输出方程,画出串行数据图检测器的 逻辑图如图5-24所示。 &ID D &Y 图5-24串行数据检测器的逻辑图
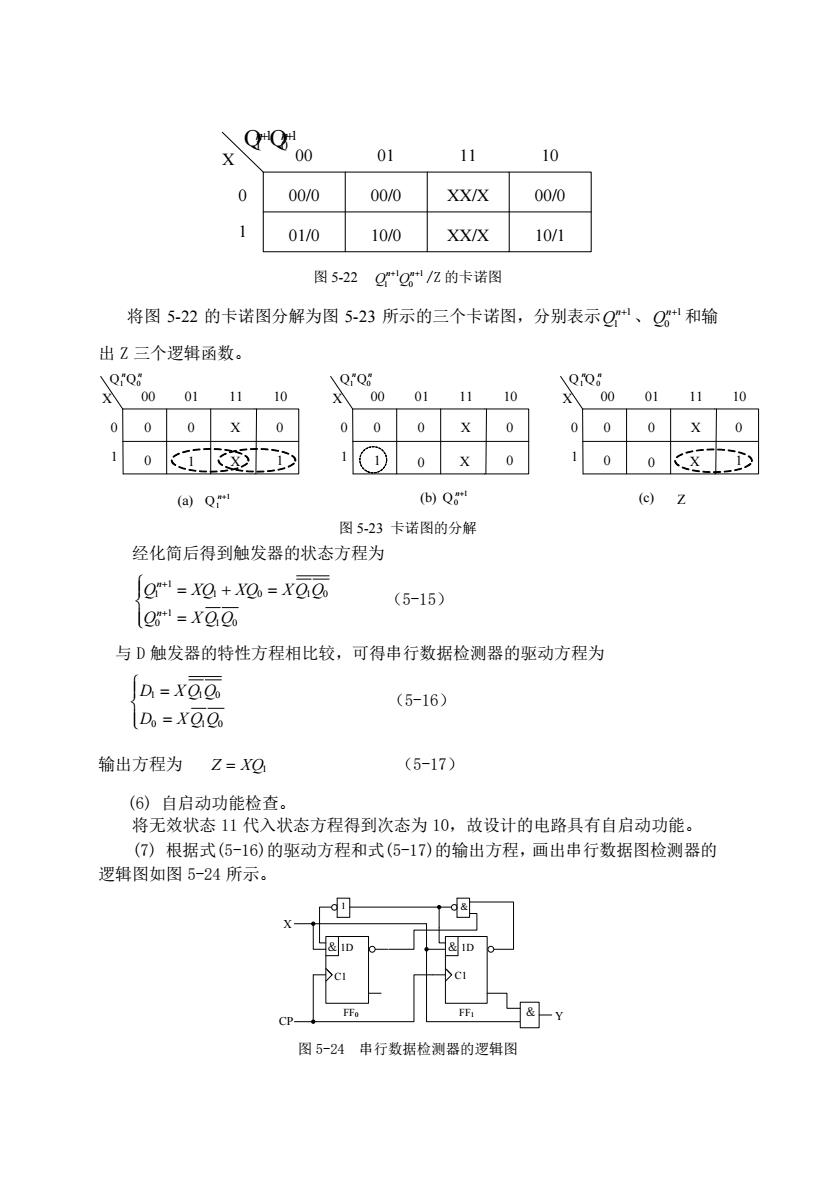
00/0 00/0 00/0 01/0 10/0 10/1 XX/X XX/X 0 1 X 00 01 11 10 1 1 Q Q1 0 n n + + 图 5-22 1 1 1 0 n n Q Q+ + /Z 的卡诺图 将图 5-22 的卡诺图分解为图 5-23 所示的三个卡诺图,分别表示 1 1 n Q + 、 1 0 n Q + 和输 出 Z 三个逻辑函数。 0 0 0 0 1 1 X X 0 1 X 00 01 11 10 n n Q1 Q0 1 1 n+ (a) Q 0 0 0 1 0 X X 0 1 X 00 01 11 10 n n Q1 Q0 (b) 0 1 0 n+ Q 0 0 0 0 1 X X 0 1 X 00 01 11 10 n n Q1Q0 0 (c) Z 图 5-23 卡诺图的分解 经化简后得到触发器的状态方程为 1 1 1 0 1 0 1 0 1 0 n n Q XQ XQ X Q Q Q X Q Q + + = + = = (5-15) 与 D 触发器的特性方程相比较,可得串行数据检测器的驱动方程为 1 1 0 0 1 0 D X Q Q D X Q Q = = (5-16) 输出方程为 Z XQ = 1 (5-17) (6) 自启动功能检查。 将无效状态 11 代入状态方程得到次态为 10,故设计的电路具有自启动功能。 (7) 根据式(5-16)的驱动方程和式(5-17)的输出方程,画出串行数据图检测器的 逻辑图如图 5-24 所示。 & C1 1D & C1 1D & Y 1 & FF0 FF1 CP X 图 5-24 串行数据检测器的逻辑图

5.2计数器 5.2.1计数器的特点和分类 计数器一一用以统计输入脉冲CP个数的电路。计数器累计输入脉冲的最大数目 称为计数器的“模”,用M表示。计数器的“模”实际上为电路的有效状态数。 计数器的分类: 按计数进制可分为二进制计数器和非二进制计数器。非二进制计数器中最典型的 是十进制计数器。 按数字的增减趋势可分为加法计数器、减法计数器和可逆计数器。 按计数器中触发器翻转是否与计数脉冲同步分为同步计数器和异步计数器。 5.2.2异步计数器 一、异步二进制计数器 1、异步二进制加法计数器 图5-25所示为由4个下降沿触发的JK触发器组成的4位异步二进制加法计数器 的逻辑图。图中K触发器都接成T'触发器(即=K=1)。最低位触发器FF。的时钟 脉冲输入端接计数脉冲CP,其他触发器的时钟脉冲输入端接相邻低位触发器的Q端。 e: 2o 计数冲 B洁零 图5-25由JK触发器组成的4位异步二进制加法计数器的逻辑图 该电路的时序波形图如图5-26所示,状态图如图5-27所示。由状态图可见,从 初态0000(由清零脉冲所置)开始,每输入一个计数脉冲,计数器的状态按二进制加 法规律加1,所以是二进制加法计数器(4位)。又因为该计数器有0000~1111共16 个状态,所以也称16进制(1位)加法计数器或模16(M=16)加法计数器
5.2 计数器 5.2.1 计数器的特点和分类 计数器——用以统计输入脉冲 CP 个数的电路。计数器累计输入脉冲的最大数目 称为计数器的“模”,用 M 表示。计数器的“模”实际上为电路的有效状态数。 计数器的分类: 按计数进制可分为二进制计数器和非二进制计数器。非二进制计数器中最典型的 是十进制计数器。 按数字的增减趋势可分为加法计数器、减法计数器和可逆计数器。 按计数器中触发器翻转是否与计数脉冲同步分为同步计数器和异步计数器。 5.2.2 异步计数器 一、异步二进制计数器 1、异步二进制加法计数器 图 5-25 所示为由 4 个下降沿触发的 JK 触发器组成的 4 位异步二进制加法计数器 的逻辑图。图中 JK 触发器都接成 T’触发器(即 J=K=1)。最低位触发器 FF0 的时钟 脉冲输入端接计数脉冲 CP,其他触发器的时钟脉冲输入端接相邻低位触发器的 Q 端。 1J 1K C1 Q2 Q1 CP FF3 R ∧ 1K FF2 1J C1 R ∧ 1K FF1 Q 1J 0 C1 R ∧ R FF0 ∧ 1J C1 1K Q3 1 CR 计数脉冲 清零脉冲 Q Q Q Q 图 5-25 由 JK 触发器组成的 4 位异步二进制加法计数器的逻辑图 该电路的时序波形图如图 5-26 所示,状态图如图 5-27 所示。由状态图可见,从 初态 0000(由清零脉冲所置)开始,每输入一个计数脉冲,计数器的状态按二进制加 法规律加 1,所以是二进制加法计数器(4 位)。又因为该计数器有 0000~1111 共 16 个状态,所以也称 16 进制(1 位)加法计数器或模 16(M=16)加法计数器