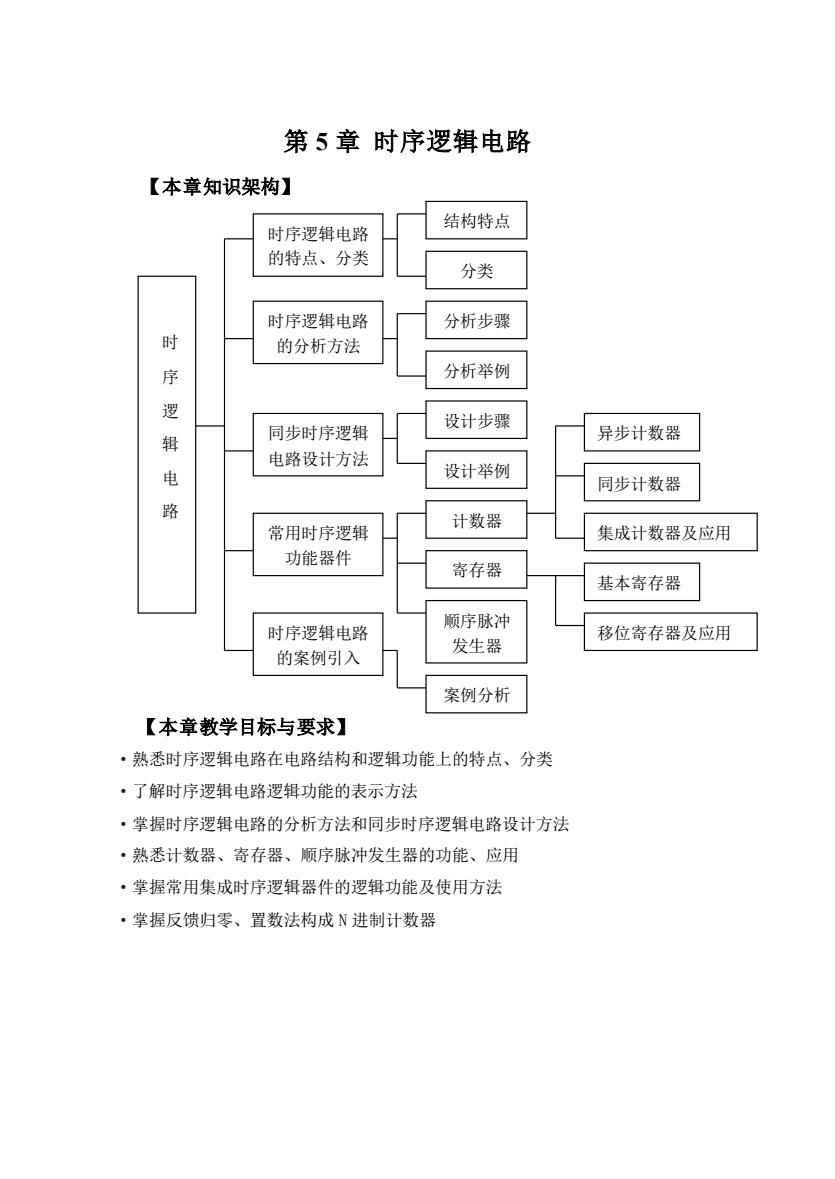
第5章时序逻辑电路 【本章知识架构】 时序逻辑电路 结构特点 的特点、分类 分类 时序逻辑电路 分析步骤 多 的分析方法 序 分析举例 色 同先时序罗据 设计步骤 辑 异步计数器 电路设计万法 电 设计举例 同步计数器 路 常用时序逻辑 计数器 集成计数器及应用 功能器件 寄存器 基本寄存器 顺序脉冲 时序罗辑电路 移位寄存器及应用 发生器 的案例引入 案例分析 【本章教学目标与要求】 ·熟悉时序逻辑电路在电路结构和逻辑功能上的特点、分类 ·了解时序逻辑电路逻辑功能的表示方法 ·掌握时序逻辑电路的分析方法和同步时序逻辑电路设计方法 ·熟悉计数器、寄存器、顺序脉冲发生器的功能、应用 ·掌握常用集成时序逻辑器件的逻辑功能及使用方法 ·掌握反馈归零、置数法构成N进制计数器
第 5 章 时序逻辑电路 【本章知识架构】 【本章教学目标与要求】 ·熟悉时序逻辑电路在电路结构和逻辑功能上的特点、分类 ·了解时序逻辑电路逻辑功能的表示方法 ·掌握时序逻辑电路的分析方法和同步时序逻辑电路设计方法 ·熟悉计数器、寄存器、顺序脉冲发生器的功能、应用 ·掌握常用集成时序逻辑器件的逻辑功能及使用方法 ·掌握反馈归零、置数法构成 N 进制计数器 时 序 逻 辑 电 路 时序逻辑电路 的特点、分类 时序逻辑电路 的分析方法 同步时序逻辑 电路设计方法 常用时序逻辑 功能器件 结构特点 分类 分析步骤 分析举例 设计步骤 设计举例 计数器 寄存器 时序逻辑电路 的案例引入 案例分析 异步计数器 同步计数器 集成计数器及应用 顺序脉冲 发生器 基本寄存器 移位寄存器及应用
5.1概述 5.1.1时序逻辑电路的结构特点 时序逻辑电路:电路任何一时刻的输出状态不仅与该时刻的输入信号有关,而且 还与电路的原状态有关。时序电路中含有具有记忆能力的存储器件(最常用的是触发 器)和反馈通道。 JK触发器就是一个最简单的时序电路。 例如:JK触发器,其特征方程:Q1=JQ+KQ。Q1和当前的输入人、K有关, 还与过去的Q有关。 由触发器作存储器件的时序电路的结构框图如图51所示,一般来说,它由组合 电路和触发器两部分组成。 输入五 Z1输出 信号 组合电路 信号 触发器 触发器 输出信号 电路 -CP 图51时序逻辑电路框图 5.1.2时序逻辑电路的分类 按照电路状态变化的特点,时序电路分为同步时序电路和异步时序电路两大类。 同步时序电路内部触发器的状态更新在时钟脉冲作用下是同时进行的,即电路中 有一个统一的时钟脉冲,每来一个时钟脉冲,电路的状态只改变一次。 异步时序电路各个触发器的时钟脉冲不同,即电路中没有统一的时钟脉冲来控制 电路状态的变化,电路状态改变时,电路中要更新状态的触发器的翻转有先有后,是 异步进行的。 按照电路中输出变量是否和输入变量直接相关,时序电路又分为米里(Mey)型 电路和摩尔(Moore)型电路。 米里型电路的外部输出Z既与触发器的状态Q”有关,又与外部输入X有关。而
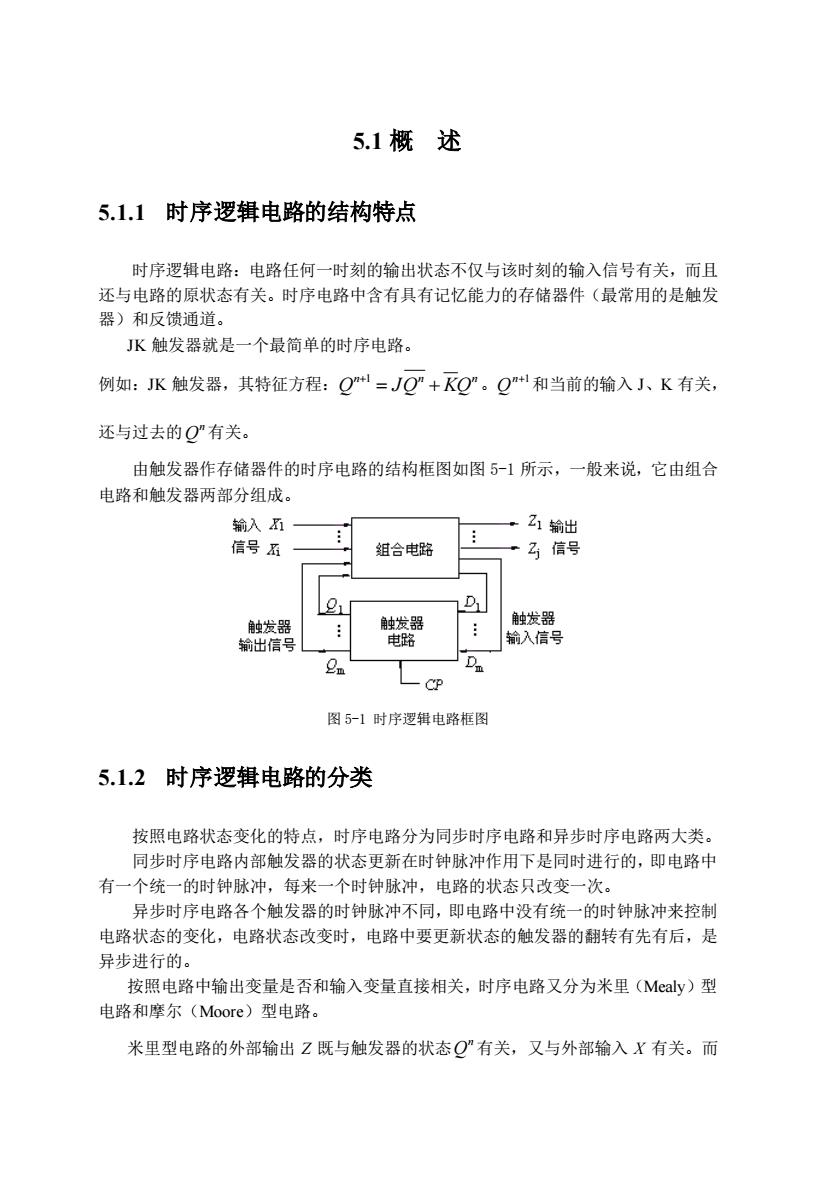
5.1 概 述 5.1.1 时序逻辑电路的结构特点 时序逻辑电路:电路任何一时刻的输出状态不仅与该时刻的输入信号有关,而且 还与电路的原状态有关。时序电路中含有具有记忆能力的存储器件(最常用的是触发 器)和反馈通道。 JK 触发器就是一个最简单的时序电路。 例如:JK 触发器,其特征方程: n n n 1 Q JQ KQ + = + 。 n 1 Q + 和当前的输入 J、K 有关, 还与过去的 n Q 有关。 由触发器作存储器件的时序电路的结构框图如图 5-1 所示,一般来说,它由组合 电路和触发器两部分组成。 图 5-1 时序逻辑电路框图 5.1.2 时序逻辑电路的分类 按照电路状态变化的特点,时序电路分为同步时序电路和异步时序电路两大类。 同步时序电路内部触发器的状态更新在时钟脉冲作用下是同时进行的,即电路中 有一个统一的时钟脉冲,每来一个时钟脉冲,电路的状态只改变一次。 异步时序电路各个触发器的时钟脉冲不同,即电路中没有统一的时钟脉冲来控制 电路状态的变化,电路状态改变时,电路中要更新状态的触发器的翻转有先有后,是 异步进行的。 按照电路中输出变量是否和输入变量直接相关,时序电路又分为米里(Mealy)型 电路和摩尔(Moore)型电路。 米里型电路的外部输出 Z 既与触发器的状态 n Q 有关,又与外部输入 X 有关。而

摩尔型电路的外部输出Z仅与触发器的状态Q”有关,而与外部输入X无关。 5.1.3时序电路逻辑功能的表示方法 时序电路的逻辑功能可用逻辑表达式、状态表、卡诺图、状态图、时序图和逻辑 图等六种方式表示,这些表示方法在本质上是相同的,可以互相转换。 5.2时序电路的分析和设计方法 5.2.1时序电路的分析方法 1.时序电路的一般分析步骤 (1)根据给定的时序电路图写出下列各逻辑方程式: 时钟方程。各触发器时钟端的逻辑表达式(对于同步时序电路这一步可省略)。 输出方程。时序电路的输出逻辑表达式,通常为现态和输入变量的函数。 驱动方程。各触发器输入端的逻辑表达式。 (2)将驱动方程代入相应触发器的特性方程,求得各触发器的次态方程,也就是 时序电路的状态方程。 (3)根据状态方程和输出方程,列出该时序电路的状态表,画出状态图或时序图。 (4)根据电路的状态表或状态图说明给定时序电路的逻辑功能。 2。同步时序电路的分析举例 【例5-1】试分析图53所示的时序电路 Q o.& 图53【例51】逻辑电路图 解:由于图53为同步时序电路,图中的三个触发器都接至同一个时钟脉冲源CP, 所以各触发器的时钟方程可以不写。该电路为Moor心型同步时序电路。 (1)写出输出方程:Z=Q”·Q (5-1)
摩尔型电路的外部输出 Z 仅与触发器的状态 n Q 有关,而与外部输入 X 无关。 5.1.3 时序电路逻辑功能的表示方法 时序电路的逻辑功能可用逻辑表达式、状态表、卡诺图、状态图、时序图和逻辑 图等六种方式表示,这些表示方法在本质上是相同的,可以互相转换。 5.2 时序电路的分析和设计方法 5.2.1 时序电路的分析方法 1.时序电路的一般分析步骤 (1)根据给定的时序电路图写出下列各逻辑方程式: 时钟方程。各触发器时钟端的逻辑表达式(对于同步时序电路这一步可省略)。 输出方程。时序电路的输出逻辑表达式,通常为现态和输入变量的函数。 驱动方程。各触发器输入端的逻辑表达式。 (2)将驱动方程代入相应触发器的特性方程,求得各触发器的次态方程,也就是 时序电路的状态方程。 (3)根据状态方程和输出方程,列出该时序电路的状态表,画出状态图或时序图。 (4)根据电路的状态表或状态图说明给定时序电路的逻辑功能。 2.同步时序电路的分析举例 【例 5-1】试分析图 5-3 所示的时序电路 图 5-3 【例 5-1】逻辑电路图 解:由于图 5-3 为同步时序电路,图中的三个触发器都接至同一个时钟脉冲源 CP, 所以各触发器的时钟方程可以不写。该电路为 Moore 型同步时序电路。 (1)写出输出方程: 1 2 n n Z Q Q = (5-1)
(2)写出驱动方程: Jo=oro: =0: [52=0Q(5-2) K=1 K=010: K:=0" (3)写出JK触发器的特性方程Q=JQ+KQ,然后将各驱动方程代入JK 触发器的特性方程,得各触发器的次态方程: o=Joo:+Koo:=0foro: o"M=Jo"+K.o"=o"o"+o"o"o" (5-3) O=J2O:+Ko =OrO"O;+0"O" (4)作状态转换表及状态图 设触发器的初始状态QQ”Q=000,代入式(5-1)和(5-3),得到新的一组状态和 输出,再将这组状态作为触发器的现态,分析下一个时钟脉冲到来后时序电路的次态 和输出,依次可以得到表5-1所示的状态转换表。 表5-1 现态 次 态 输出 oo o; 0:"Q""Q" Z 00 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 完整的状态转换图如图5-4所示。 000 /0 0 +001 /0 -(011 110 101 /0 0 (100 图5-4【例6-1】状态转换图 (5)画时序图
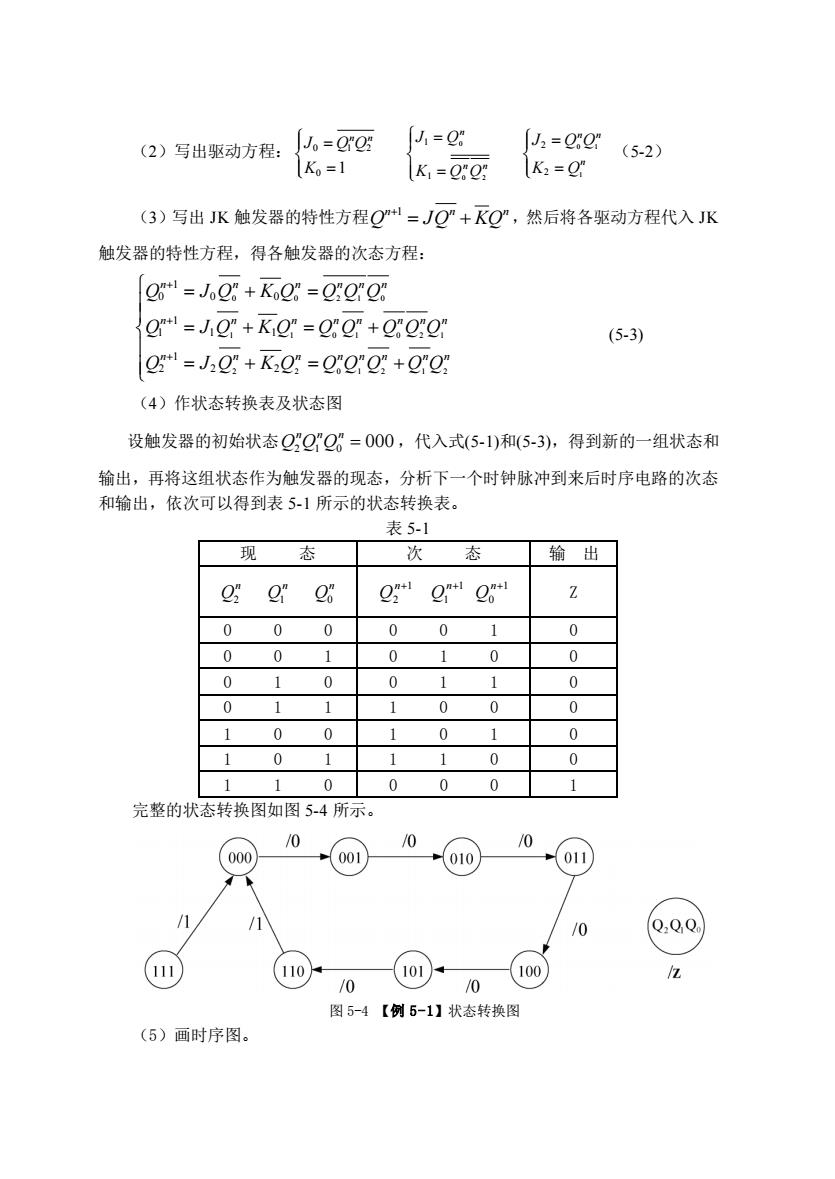
(2)写出驱动方程: 0 1 2 0 1 n n J Q Q K = = 0 0 2 1 1 n n n J Q K Q Q = = 0 1 1 2 2 n n n J Q Q K Q = = (5-2) (3)写出 JK 触发器的特性方程 n n n 1 Q JQ KQ + = + ,然后将各驱动方程代入 JK 触发器的特性方程,得各触发器的次态方程: 0 0 2 1 0 1 1 0 1 0 2 1 2 2 0 1 2 1 2 1 0 0 0 1 1 1 1 1 2 2 2 n n n n n n n n n n n n n n n n n n n n n n Q J Q K Q Q Q Q Q J Q K Q Q Q Q Q Q Q J Q K Q Q Q Q Q Q + + + = + = = + = + = + = + (5-3) (4)作状态转换表及状态图 设触发器的初始状态 2 1 0 000 nnn QQQ = ,代入式(5-1)和(5-3),得到新的一组状态和 输出,再将这组状态作为触发器的现态,分析下一个时钟脉冲到来后时序电路的次态 和输出,依次可以得到表 5-1 所示的状态转换表。 表 5-1 现 态 次 态 输 出 2 n Q 1 n Q 0 n Q 1 2 n Q + 1 1 n Q + 1 0 n Q + Z 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 1 1 0 0 1 1 1 0 0 0 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0 0 0 1 完整的状态转换图如图 5-4 所示。 图 5-4 【例 5-1】状态转换图 (5)画时序图
如图5-5所示。 CP 9 图5-5【例5-1】时序图 (6)逻辑功能分析 从状态转换表和状态转换图可以看出,当触发器的状态为Q226=110,下 个时钟脉冲到来后电路的次态QQQ=000,电路回到了设定的初始状态。 因此,在以后的时钟脉冲作用下,逻辑电路的状态和输出必然按表51所示的顺序反 复循环。每次状态到达110时,输出Z=1,故该电路是一个同步七进制计数器,输出 Z为计数器的进位信号。 三个触发器共有八种状态取值,七进制计数器只使用其中七种状态构成有效循 环,其中状态111没有用到,称为无效状态。将QQ=111作为初始状态代入式 (5-3)中,求得其次态Q+QQ1=000,其次态为有效循环状态 【例5-2】试分析图56所示的时序逻辑电路 图5-6【例5-2】逻辑电路图 解:由于图56为同步时序电路,图中的两个触发器都接至同一个时钟脉冲源CP, 所以各触发器的时钟方程可以不写。该电路为Mealy型同步时序逻辑电路。 (1)写出输出方程:Z=(X⊕Q")Q (5.4)
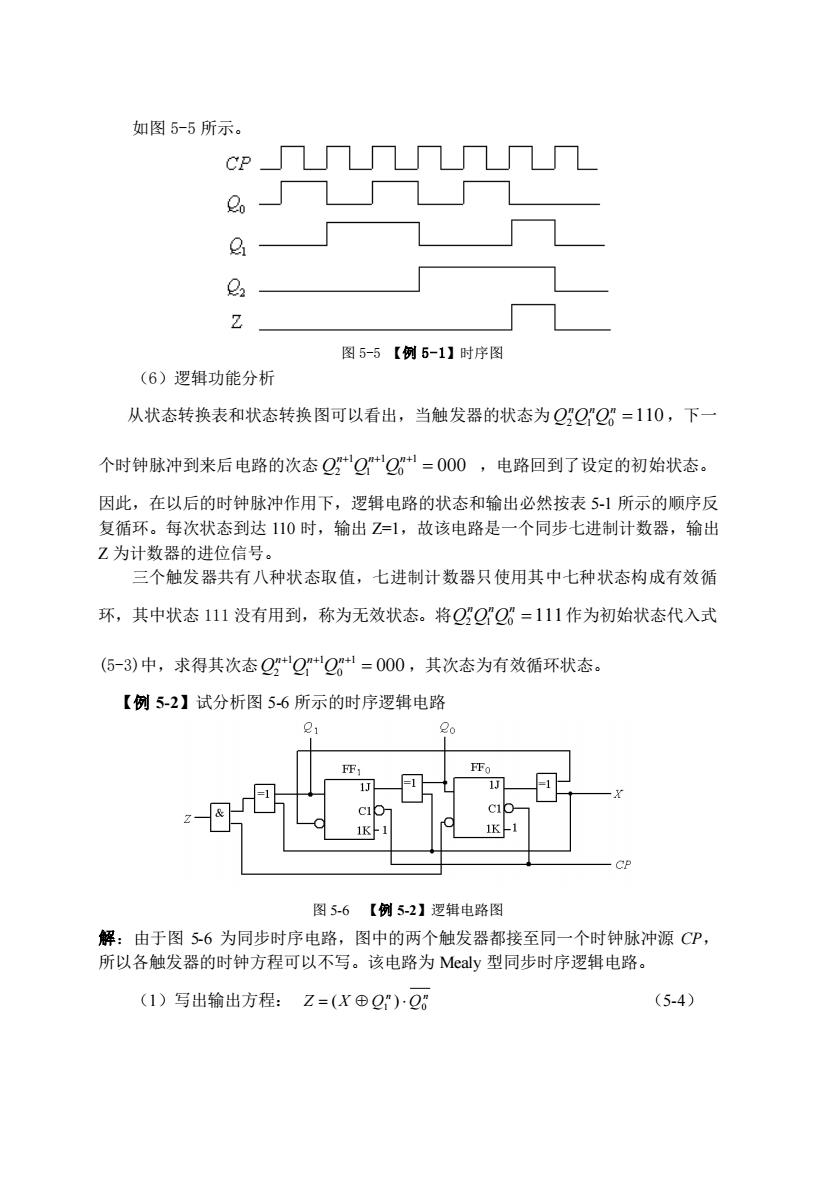
如图 5-5 所示。 图 5-5 【例 5-1】时序图 (6)逻辑功能分析 从状态转换表和状态转换图可以看出,当触发器的状态为 2 1 0 110 nnn QQQ = ,下一 个时钟脉冲到来后电路的次态 111 2 1 0 000 nnn QQQ +++ = ,电路回到了设定的初始状态。 因此,在以后的时钟脉冲作用下,逻辑电路的状态和输出必然按表 5-1 所示的顺序反 复循环。每次状态到达 110 时,输出 Z=1,故该电路是一个同步七进制计数器,输出 Z 为计数器的进位信号。 三个触发器共有八种状态取值,七进制计数器只使用其中七种状态构成有效循 环,其中状态 111 没有用到,称为无效状态。将 2 1 0 111 nnn QQQ = 作为初始状态代入式 (5-3)中,求得其次态 111 2 1 0 000 nnn QQQ +++ = ,其次态为有效循环状态。 【例 5-2】试分析图 5-6 所示的时序逻辑电路 图 5-6 【例 5-2】逻辑电路图 解:由于图 5-6 为同步时序电路,图中的两个触发器都接至同一个时钟脉冲源 CP, 所以各触发器的时钟方程可以不写。该电路为 Mealy 型同步时序逻辑电路。 (1)写出输出方程: n n Z X Q1 Q0 = ( ) (5-4)