
(2)写出驱动方程: J=X⊕g (5-5a) K=1 J=X⊕06 (5-5b) K=1 (3)写出JK触发器的特性方程Q=Jg+,然后将各驱动方程代入JK触 发器的特性方程,得各触发器的次态方程: Q。=JQ6+KQ6=(X⊕g)g6 (5-6a) Q=J,2"+Kg=(X⊕Q)-g (5-6b (4)作状态转换表及状态图 由于输入控制信号X可取1,也可取0,所以分两种情况列状态转换表和画状态 图。 ①当X0时。 将-0代入输出方程(5-4)和触发器的次态方程(5-6),则输出方程简化为: Z=gg:触发器的次态方程简化为:Q,”-gQ,g=Qgg(5-7) 设电路的现态为Q?=00,依次代入上述触发器的次态方程和输出方程中进行计 算,得到电路的状态转换表如表5-2所示。 根据表5-2所示的状态转换表可得状态转换图如图5-7所示。 (eP 表5-2X0时的状态表 现态 次态 输出 四”0”0 g1Q6 0 0 图570时的状态图 0 ②当=1时。 10 输出方程简化为:Z=Q: 0 0 触发器的次态方程简化为: Q。=grg,g=gg (5-8) 计算可得电路的状态转换表如表5-3所示,状态图如图5-8所示
(2)写出驱动方程: 0 1 0 1 n J X Q K = = (5-5 a) 1 0 1 1 n J X Q K = = (5-5b) (3)写出 JK 触发器的特性方程 n n n Q = JQ + KQ +1 ,然后将各驱动方程代入 JK 触 发器的特性方程,得各触发器的次态方程: n n n n n Q J 0 Q0 K0Q0 X Q1 Q0 1 0 = + = ( ) + (5-6a) n n n n n Q J1Q1 K1Q1 X Q0 Q1 1 1 = + = ( ) + (5-6b) (4)作状态转换表及状态图 由于输入控制信号 X 可取 1,也可取 0,所以分两种情况列状态转换表和画状态 图。 ①当 X=0 时。 将 X=0 代入输出方程(5-4)和触发器的次态方程(5-6),则输出方程简化为: n n Z = Q1 Q0 ;触发器的次态方程简化为: n n n Q Q1 Q0 1 0 = + , n n n Q Q0 Q1 1 1 = + (5-7) 设电路的现态为 1 0 = 00 n n Q Q ,依次代入上述触发器的次态方程和输出方程中进行计 算,得到电路的状态转换表如表 5-2 所示。 根据表 5-2 所示的状态转换表可得状态转换图如图 5-7 所示。 ②当 X=1 时。 输出方程简化为: n n Z = Q1 Q0 ; 触发器的次态方程简化为: n n n Q Q1 Q0 1 0 = + , n n n Q Q0 Q1 1 1 = + (5-8) 计算可得电路的状态转换表如表 5-3 所示,状态图如图 5-8 所示。 表 5-2 X=0 时的状态表 现 态 次态 输出 n Q1 n Q0 1 1 n+ Q 1 0 n+ Q Z 0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 图 5-7 X=0 时的状态图
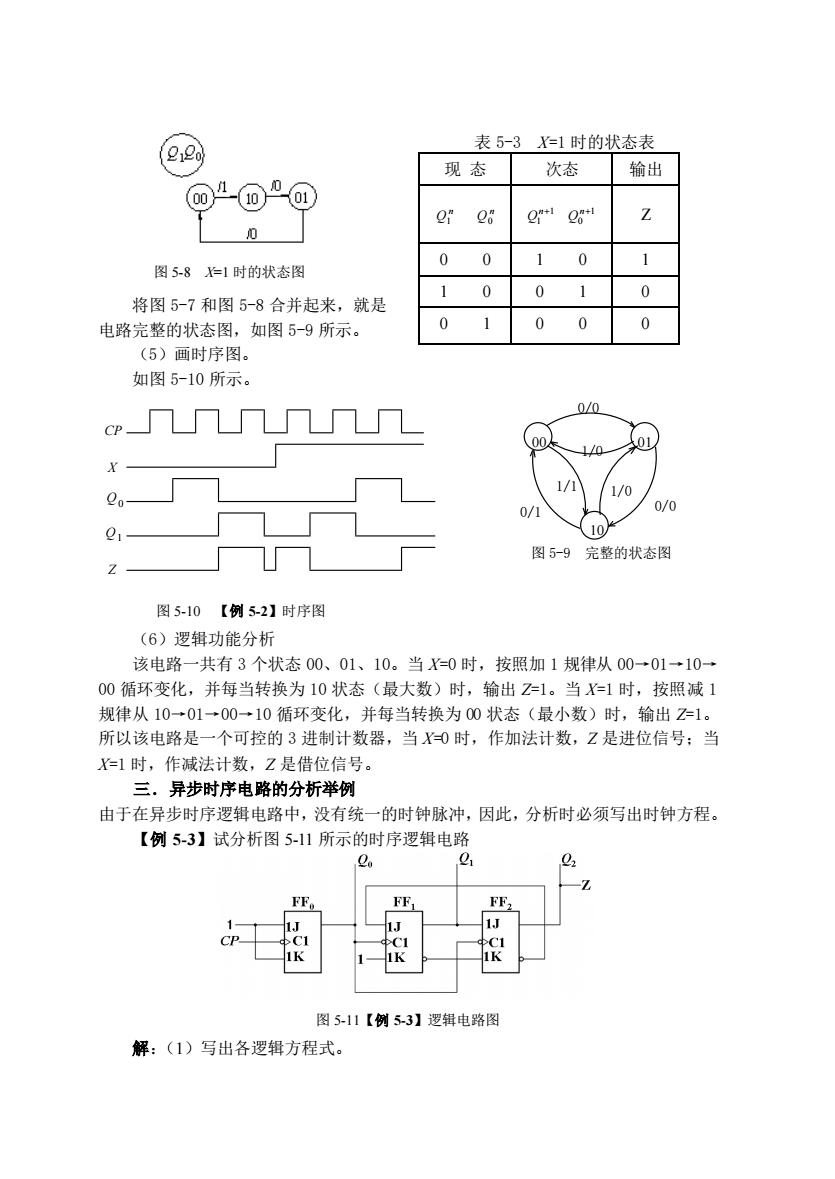
( 表5-3=1时的状态表 现态 次态 输出 @4⑩”@ 0 00 10 1 图581时的状态图 将图5-7和图5-8合并起来,就是 10 0 0 电路完整的状态图,如图59所示。 0 1 0 0 0 (5)画时序图, 如图5-10所示。 冂Π 1/八 1/0 21 10 图59完整的状态图 图5-10【例52】时序图 (6)逻辑功能分析 该电路一共有3个状态00、01、10。当X=0时,按照加1规律从00一01一10 00循环变化,并每当转换为10状态(最大数)时,输出Z=1。当=1时,按照减1 规律从10一01→00一10循环变化,并每当转换为00状态(最小数)时,输出2=1。 所以该电路是一个可控的3进制计数器,当X0时,作加法计数,Z是进位信号:当 X1时,作减法计数,Z是借位信号。 三。异步时序电路的分析举例 由于在异步时序逻辑电路中,没有统一的时钟脉冲,因此,分析时必须写出时钟方程。 【例5-3】试分析图5-11所示的时序逻辑电路 图5-11【例5-3】逻辑电路图 解:(1)写出各逻辑方程式
将图 5-7 和图 5-8 合并起来,就是 电路完整的状态图,如图 5-9 所示。 (5)画时序图。 如图 5-10 所示。 Q1 Q0 X CP Z 图 5-10 【例 5-2】时序图 (6)逻辑功能分析 该电路一共有 3 个状态 00、01、10。当 X=0 时,按照加 1 规律从 00→01→10→ 00 循环变化,并每当转换为 10 状态(最大数)时,输出 Z=1。当 X=1 时,按照减 1 规律从 10→01→00→10 循环变化,并每当转换为 00 状态(最小数)时,输出 Z=1。 所以该电路是一个可控的 3 进制计数器,当 X=0 时,作加法计数,Z 是进位信号;当 X=1 时,作减法计数,Z 是借位信号。 三.异步时序电路的分析举例 由于在异步时序逻辑电路中,没有统一的时钟脉冲,因此,分析时必须写出时钟方程。 【例 5-3】试分析图 5-11 所示的时序逻辑电路 图 5-11【例 5-3】逻辑电路图 解:(1)写出各逻辑方程式。 表 5-3 X=1 时的状态表 现 态 次态 输出 n Q1 n Q0 1 1 n+ Q 1 0 n+ Q Z 0 0 1 0 1 1 0 0 1 0 0 1 0 0 0 图 5-8 X=1 时的状态图 00 01 10 0/0 0/0 0/1 1/1 1/0 1/0 图 5-9 完整的状态图

①时钟方程: CP=CP(FF。由CP下降沿触发) CP=CP=Q(FE、FE由O下降沿触发) ②输出方程:Z=Q (5-9) ③各触发器的驱动方程: J0=K=1:J=g3,K,=1:J2=Q,K2=g (5-10) (2)将各驱动方程代入JK触发器的特性方程,得各触发器的次态方程: Q=Jog"+K2"=1Q"+1Q"=0 O"M=Jo+Ko"=0:o+1.0"=0.o" (5-1) OM=J2o+k.o"=0"O"+o"o"=0"o+o"o"=o" (3)作状态转换表、状态图、时序图 表5-4状态转换表 现态 次态 输出 时钟脉冲 Q:of 08 g1g106 2 CP2 CP CPo 000 001 0 00 1 01 0 0 ↓↓ 0 1 0 0 1 1 0 ↑↓ 0 1 1 0 0 ↓ 100 1 0 1 10 1 0 0 0 根据状态转换表可得状态转换图如图5-12所示,时序图如图5-13所示。 200)n @“@①@@@ 11
①时钟方程: CP CP 0 = ( FF0 由 CP 下降沿触发) CP CP Q 1 2 0 = = ( FF1、 FF2 由 Q0 下降沿触发) ②输出方程: 2 n Z Q= (5-9) ③各触发器的驱动方程: 0 0 J K= =1 ; 1 2 1 , 1 n J Q K = = ; 2 1 2 1 , n n J Q K Q = = (5-10) (2)将各驱动方程代入 JK 触发器的特性方程,得各触发器的次态方程: 1 1 1 1 1 1 1 2 1 1 2 1 2 2 1 2 1 2 1 2 1 2 1 1 0 0 0 1 1 1 1 1 2 2 3 1 1 1 n n n n n n n n n n n n n n n n n n n n n n n n n n Q J Q K Q Q Q Q Q J Q K Q Q Q Q Q Q Q J Q K Q Q Q Q Q Q Q Q Q Q + + + = + = + = = + = + = = + = + = + = (5-11) (3)作状态转换表、状态图、时序图 表 5-4 状态转换表 现态 次态 输出 时钟脉冲 2 n Q n Q1 n Q0 1 2 n Q + 1 1 n+ Q 1 0 n+ Q Z CP2 CP1 CP0 0 0 0 0 0 1 0 ↑ ↑ ↓ 0 0 1 0 1 0 0 ↓ ↓ ↓ 0 1 0 0 1 1 0 ↑ ↑ ↓ 0 1 1 1 0 0 0 ↓ ↓ ↓ 1 0 0 1 0 1 1 ↑ ↑ ↓ 1 0 1 0 0 0 1 ↓ ↓ ↓ 根据状态转换表可得状态转换图如图 5-12 所示,时序图如图 5-13 所示

图5-12【例53】状态图 2 图513【例53】时序图 (5)逻辑功能分析 由状态图可知:该电路一共有6个状态,在时钟脉冲作用下,按照加1规律循环 变化,所以是一个异步六进制加法计数器,Z是进位信号,向高位送出一个负跃变的 进位信号。 5.1.2同步时序电路的设计方法 一,同步时序电路的设计步骤 1.根据设计要求,设定状态,导出对应状态转换图或状态转换表。根据设计的具 体要求,确定时序逻辑电路输入变量、输出变量和状态,确定输入变量、输出变量和 状态的含义,以及在时钟脉冲作用下状态之间的转换关系,并标出其相应的转换条件 和输出,用状态转换图或状态转换表来表示。 2.状态化简。原始状态图(表)通常不是最简的,往往可以消去一些多余状态。 消去多余状态的过程叫做状态化简。输入相同时、输出相同、且转换的状态也相同的 状态叫做等价状态。设Si和Sj是原始状态转换图或状态转换表的两个状态,若Si和 Sj在相同的输入信号作用下具有相同的输出,并且可以转换到相同的状态中去,则称 状态Si和状态Sj等价。显然等价状态是冗余的,可以合并为一个状态 3.选择触发器的类型和个数。电路的状态数确定以后,需要确定电路设计所用触 发器的类型和个数。一般来说,选用触发器的功能越强大,则设计的电路越简单。因 为n个触发器共2”个状态组合,所以触发器的个数根据下式确定:2-≤M≤2” 式中:M为电路的状态数,n为所需要触发器的个数。 4.状态分配(状态编码)。触发器的个数确定以后,状态变量的个数也随之确定 如三个触发器有三个状态变量,共有八种取值:000~111。给电路中的每一个状态选 取不同取值代码的过程称为状态编码,也称为状态分配。状态编码完成后,由逻辑抽
图 5-12 【例 5-3】状态图 图 5-13 【例 5-3】时序图 (5)逻辑功能分析 由状态图可知:该电路一共有 6 个状态,在时钟脉冲作用下,按照加 1 规律循环 变化,所以是一个异步六进制加法计数器,Z 是进位信号,向高位送出一个负跃变的 进位信号。 5.1.2 同步时序电路的设计方法 一.同步时序电路的设计步骤 1.根据设计要求,设定状态,导出对应状态转换图或状态转换表。根据设计的具 体要求,确定时序逻辑电路输入变量、输出变量和状态,确定输入变量、输出变量和 状态的含义,以及在时钟脉冲作用下状态之间的转换关系,并标出其相应的转换条件 和输出,用状态转换图或状态转换表来表示。 2.状态化简。原始状态图(表)通常不是最简的,往往可以消去一些多余状态。 消去多余状态的过程叫做状态化简。输入相同时、输出相同、且转换的状态也相同的 状态叫做等价状态。设 Si 和 Sj 是原始状态转换图或状态转换表的两个状态,若 Si 和 Sj 在相同的输入信号作用下具有相同的输出,并且可以转换到相同的状态中去,则称 状态 Si 和状态 Sj 等价。显然等价状态是冗余的,可以合并为一个状态。 3.选择触发器的类型和个数。电路的状态数确定以后,需要确定电路设计所用触 发器的类型和个数。一般来说,选用触发器的功能越强大,则设计的电路越简单。因 为 n 个触发器共 2 n 个状态组合,所以触发器的个数根据下式确定: 1 2 2 n n M − 式中:M 为电路的状态数,n 为所需要触发器的个数。 4.状态分配(状态编码)。触发器的个数确定以后,状态变量的个数也随之确定。 如三个触发器有三个状态变量,共有八种取值:000~111。给电路中的每一个状态选 取不同取值代码的过程称为状态编码,也称为状态分配。状态编码完成后,由逻辑抽

象得到的状态转换图和转换表就具体化了,反映了逻辑电路在时钟脉冲作用下,触发 器状态的变化关系 为了有利于驱动方程的化简,状态编码的三个实用原则是: (①)次态相同,现态相邻,即在相同输入条件下具有相同次态的现态应分配相邻的编 码: (2②)现态相同,次态相邻,即同一现态在相邻输入条件下的不同次态应分配相邻的编 码: (3)输出相同,现态相邻,即在所有输入条件下具有相同输出的现态应分配相邻的编 码。 5.根据编码状态表以及所采用的触发器的逻辑功能,导出待设计电路的输出方程 和驱动方程。用卡诺图表示每个触发器的次态与现态及输入变量之间的关系,求出电 路的状态方程,结合选用触发器的特性方程,求出其驱动方程。用卡诺图表示输出变 量与触发器现态和输入变量之间的关系,求出电路的输出方程。 6.根据输出方程和驱动方程画出逻辑图。 7.检查电路能否自启动。若电路含有无效状态(指没有用到的多余状态),则必须 检查电路是否具有自启动功能。电路处于无效状态时,能够经过有限个时钟脉冲自动 回到有效状态中去,则称电路具有自启动功能。具有自启动功能的电路在上电时或因 干扰脱离正常状态时,能够自动返回到有效状态。自启动功能是时序逻辑电路设计的 个基本要求。 二.同步时序电路的设计举例 【例5-4】设计一个同步5进制加法计数器 解:设计步骤如下。 (1)根据设计要求,设定状态,画出状态转换图。由于是5 进制计数器,所以应有5个不同的状态,分别用S、S、.、S,表 示。在计数脉冲CP作用下,5个状态循环翻转,在状态为S时, 进位输出Z=1。状态转换图如图5-14所示。 图5-14状态图 (2)状态化简。5进制计数器应有5个状态,不须化简。 (3)状态分配,列状态转换编码表。由式2”≥W>2r可知,应采用3位二进制 代码。该计数器选用三位自然二进制加法计数编码,即S=000、S=001、·、S=100。 由此可列出状态转换表如表5-5所示。 表5-5状态转换表 现态 次态 进位输出 状态转换顺序 Q5 of Q8 gg1Q6* So 0 00 0 01 0
象得到的状态转换图和转换表就具体化了,反映了逻辑电路在时钟脉冲作用下,触发 器状态的变化关系。 为了有利于驱动方程的化简,状态编码的三个实用原则是: (1)次态相同,现态相邻,即在相同输入条件下具有相同次态的现态应分配相邻的编 码; (2)现态相同,次态相邻,即同一现态在相邻输入条件下的不同次态应分配相邻的编 码; (3)输出相同,现态相邻,即在所有输入条件下具有相同输出的现态应分配相邻的编 码。 5.根据编码状态表以及所采用的触发器的逻辑功能,导出待设计电路的输出方程 和驱动方程。用卡诺图表示每个触发器的次态与现态及输入变量之间的关系,求出电 路的状态方程,结合选用触发器的特性方程,求出其驱动方程。用卡诺图表示输出变 量与触发器现态和输入变量之间的关系,求出电路的输出方程。 6.根据输出方程和驱动方程画出逻辑图。 7.检查电路能否自启动。若电路含有无效状态(指没有用到的多余状态),则必须 检查电路是否具有自启动功能。电路处于无效状态时,能够经过有限个时钟脉冲自动 回到有效状态中去,则称电路具有自启动功能。具有自启动功能的电路在上电时或因 干扰脱离正常状态时,能够自动返回到有效状态。自启动功能是时序逻辑电路设计的 一个基本要求。 二.同步时序电路的设计举例 【例 5-4】设计一个同步 5 进制加法计数器 解:设计步骤如下。 (1)根据设计要求,设定状态,画出状态转换图。由于是 5 进制计数器,所以应有 5 个不同的状态,分别用 S0、S1、.、S4 表 示。在计数脉冲 CP 作用下,5 个状态循环翻转,在状态为 S4 时, 进位输出 Z=1。状态转换图如图 5-14 所示。 (2)状态化简。5 进制计数器应有 5 个状态,不须化简。 (3)状态分配,列状态转换编码表。由式 2 n≥N>2 n-1 可知,应采用 3 位二进制 代码。该计数器选用三位自然二进制加法计数编码,即 S0=000、S1=001、.、S4=100。 由此可列出状态转换表如表 5-5 所示。 表 5-5 状态转换表 状态转换顺序 现 态 次态 进位输出 n Q2 n Q1 n Q0 1 2 n+ Q 1 1 n+ Q 1 0 n+ Q Z S0 0 0 0 0 0 1 0 S 0 1 S 2 S S 3 4 S 图 5-14 状态图