1.3逻辑函数的表示方法及其相互之间的转换 1.3.1几种表示逻辑函数的方法 一、 真值表 将变量的各种取值与相应的函数值,以 表格的形式一一列举出来。 1.列写方法 A D 例如函数Y=AB+BC+CA 2.主要特点 优点:直观明了,便于将实际逻 辑问题抽象成数学表达式。 缺点:难以用公式和定理进行运 算和变换;变量较多时, 列函数真值表较繁琐
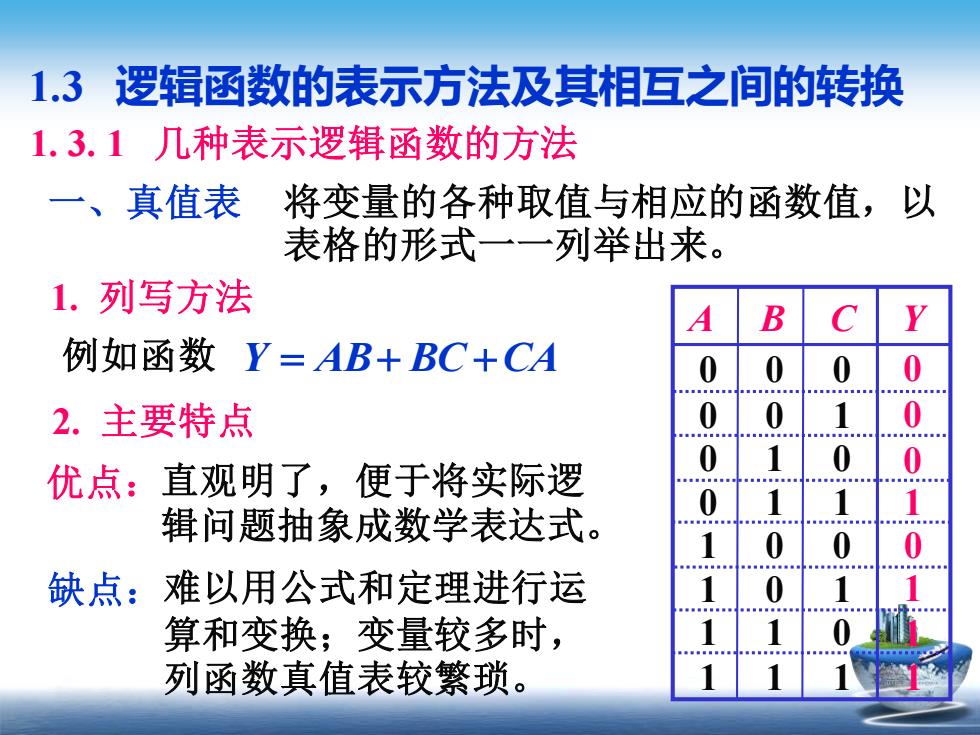
1.3 逻辑函数的表示方法及其相互之间的转换 1. 3. 1 几种表示逻辑函数的方法 一、真值表 将变量的各种取值与相应的函数值,以 表格的形式一一列举出来。 1. 列写方法 Y = AB+ BC +CA A B C Y 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 0 1 0 1 1 1 例如函数 2. 主要特点 优点:直观明了,便于将实际逻 辑问题抽象成数学表达式。 缺点:难以用公式和定理进行运 算和变换;变量较多时, 列函数真值表较繁琐

✉D☑I 二、卡诺图 真值表的一种方块图表达形式,要求变量 取值必须按照循环码的顺序排列。例如 优点:便于求出逻辑函数的最简 Y=AB+BC+CA 与或表达式。 BC 00 01 1110 A 缺点:只适于表示和化简变量个数 0 0 比较少的逻辑函数,也不便 于进行运算和变换。 0 三、逻辑表达式用与、或、非等运算表示函数中各个 变量之间逻辑关系的代数式子。 优点:书写简洁方便,易用公式和定理进行运算、变 换。 缺点: 逻辑函数较复杂时,难以直接从变量取值看拙 函数的值
三、逻辑表达式 优点:书写简洁方便,易用公式和定理进行运算、变 换。 缺点:逻辑函数较复杂时,难以直接从变量取值看出 函数的值。 二、卡诺图 A BC 0 1 00 01 11 10 1 1 1 1 0 0 0 0 优点:便于求出逻辑函数的最简 与或表达式。 缺点:只适于表示和化简变量个数 比较少的逻辑函数,也不便 于进行运算和变换。 真值表的一种方块图表达形式,要求变量 取值必须按照循环码的顺序排列。 用与、或、非等运算表示函数中各个 变量之间逻辑关系的代数式子。 Y = AB+ BC +CA 例如
四、逻辑图 用基本和常用的逻辑符号表示函数表达 式中各个变量之间的运算关系。 [例1.3.1]画出函数的逻辑图Y=AB+BC+CA 优点: & AB 最接近实际电路。 缺点: 不能进行运算 和变换,所表示的 逻辑关系不直观
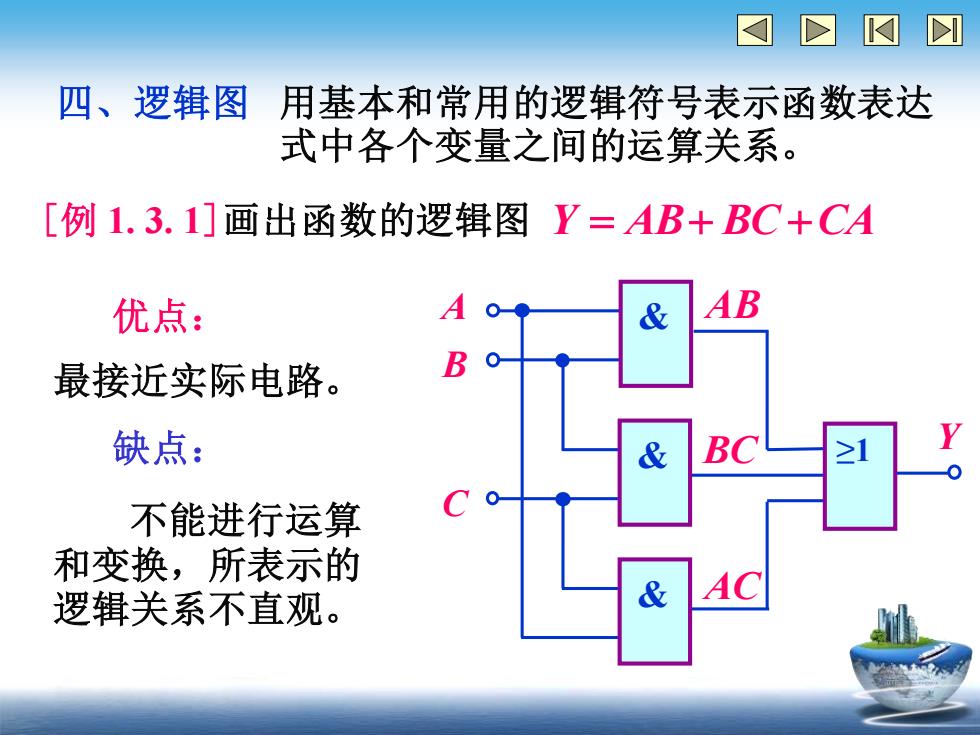
四、逻辑图 Y = AB+ BC +CA A B Y C & & 优点: 最接近实际电路。 缺点: 不能进行运算 和变换,所表示的 逻辑关系不直观。 & ABBCAC ≥1 用基本和常用的逻辑符号表示函数表达 式中各个变量之间的运算关系。 [例 1. 3. 1]画出函数的逻辑图
I 五、波形图 输入变量和对应的输出变量随时间变 化的波形。 B Y=AB 优点:形象直观地表示了变量取值与函数值在时间上 的对应关系。 缺点: 难以用公式和定理进行运算和变换,当变量个 数增多时,画图较麻烦
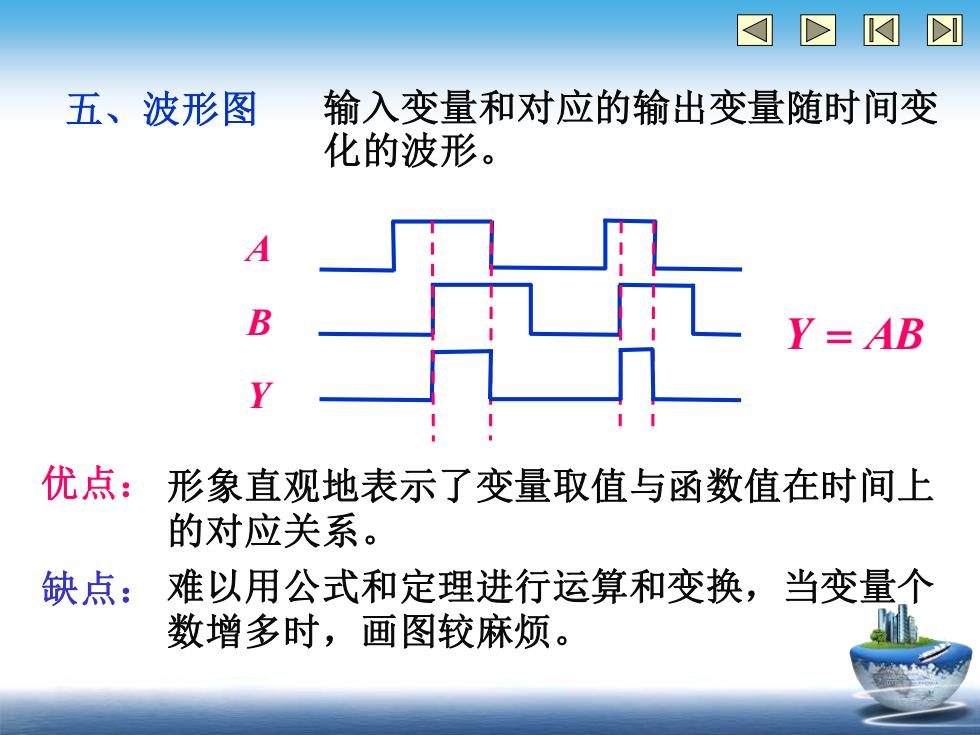
五、波形图 输入变量和对应的输出变量随时间变 化的波形。 Y = AB A B Y 优点: 形象直观地表示了变量取值与函数值在时间上 的对应关系。 缺点: 难以用公式和定理进行运算和变换,当变量个 数增多时,画图较麻烦
D 1.3.2几种表示方法之间的转换 一、真值表→函数式→逻辑图 [例]设计一个举重裁判电路。在一名主裁判(A) 和两名副裁判(B、C中,必须有两人以上(必有主 裁判)认定运动员的动作合格,试 A B 举才算成功。 0 0 ①真值表→ 0 函数式 0 0 0 0 0 将真值表中使逻辑函数Y=1的 0 1 0 输入变量取值组合所对应的最小项相 0 0 0 加,即得Y的逻辑函数式。 0 Y=ABC+ABC+ABC
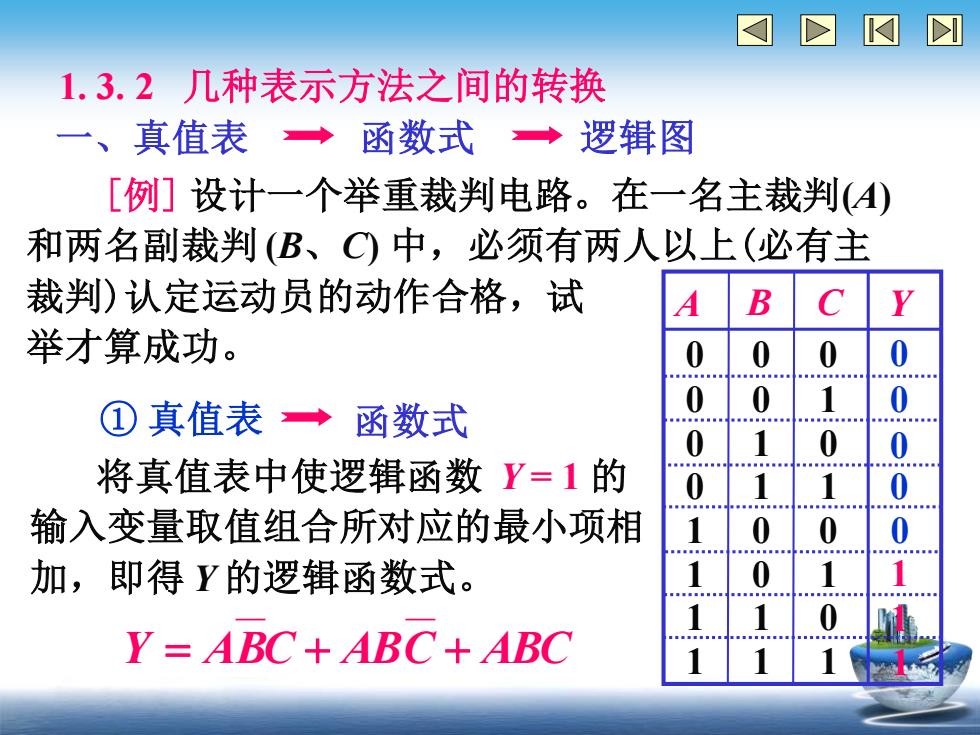
1. 3. 2 几种表示方法之间的转换 一、真值表 函数式 逻辑图 [例] 设计一个举重裁判电路。在一名主裁判(A) 和两名副裁判 (B、C) 中,必须有两人以上(必有主 裁判)认定运动员的动作合格,试 举才算成功。 ① 真值表 函数式 Y = ABC + ABC + ABC 将真值表中使逻辑函数 Y = 1 的 输入变量取值组合所对应的最小项相 加,即得 Y 的逻辑函数式。 A B C Y 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 0 0 0 1 1 1