
第1章数字逻辑基础 1.1将十进制2075和20.75转换成二进制、八进制和十六进制数。 1.2将下列各数转换成十进制数:(101.1)2,(101.1)8,(101.1)16。 1.3将二进制数110111.0101和1001101.101转换成十进制、八进制和十六进制数。 14将十进制数3692转换成二进制码及8421BCD码 1.5有一数码100100101001,作为二进制码或8421CD码时,其相应的十进制数各为多 少? 1.6利用真值表证明下列等式: ①AB+AB=(ā+BA+B) (2)A+AB+C=A+B+0 1.7在下列各个逻辑函数表达式中变量小、B、C为何值时函数值为1。 (1)Y=AB+BC+AC (2)Y=ABC+ABC+ABC+ABC (Y=(4+B+C)(4+B+C) 1.8利用公式和定理证明下列等式 (3)ABCD+ABCD=AB+BC+CD+DA 1.9将下列函数展开为最小项表达式: Y(4.B.C)= (2)Y(4.B.C,D)=AD+BCD+ 1.10用代数法将下列函数化简成为最简与或式 (1)Y=ABC+ABC+ABC+ABC (2)Y=ACD+ABD+BC+ACD+ABD (3)Y=4(4+B)+B(B+C)+B (4)Y=AB+ABC+(B+AB) (5)Y=ABC+BD(A+C)+(B+D)AC 1.11求下列函数的反函数,并将求出的反函数化简成为最简与或式 (1)Y=(4+BC+D (2)Y=4B+(4B+4B+B)C 1.12用卡诺图法将下列函数化简成为最简与或式 (1) 4D」 万+ ()Y-BCD+ABCD+BCD+ABD+AB (3)Y=(AB+BD)C+BDAC+DX(4+B)
1 第 1 章 数字逻辑基础 1.1 将十进制 2075 和 20.75 转换成二进制、八进制和十六进制数。 1.2 将下列各数转换成十进制数:(101.1)2,(101.1)8,(101.1)16。 1.3 将二进制数 110111.0101 和 1001101.101 转换成十进制、八进制和十六进制数。 1.4 将十进制数 3692 转换成二进制码及 8421BCD 码。 1.5 有一数码 100100101001,作为二进制码或 8421BCD 码时,其相应的十进制数各为多 少? 1.6 利用真值表证明下列等式: (1) AB + AB = (A+ B)(A+ B) (2) A+ A(B +C) = A+ B +C 1.7 在下列各个逻辑函数表达式中变量 A、B、C 为何值时函数值为 1。 (1) Y = AB + BC + AC (2) Y = ABC + ABC + ABC + ABC (3) Y = (A+ B +C)(A+ B +C) 1.8 利用公式和定理证明下列等式: (1) ABC + ABC + ABC = AB + AC (2) A B = A B = A B = AB + AB (3) ABCD+ ABC D = AB + BC +CD + DA 1.9 将下列函数展开为最小项表达式: (1) Y(A,B,C) = AB + AC (2) Y(A,B,C,D) = AD + BCD + ABC 1.10 用代数法将下列函数化简成为最简与或式 (1) Y = ABC + ABC + ABC + ABC (2) Y = ACD + ABD + BC + ACD + ABD (3) Y = A(A+ B) + B(B +C) + B (4) Y = AB + ABC + A(B + AB) (5) Y = ABC + BD(A+C) + (B + D)AC 1.11 求下列函数的反函数,并将求出的反函数化简成为最简与或式 (1) Y = (A + B)C + D (2) Y = AB + (AB + AB + AB)C 1.12 用卡诺图法将下列函数化简成为最简与或式 (1) Y = ABCD + ABCD + AB + AD + ABC (2) Y = BCD + ABCD + BCD + ABD + ABC (3) Y = (AB + BD)C + BDAC + D(A+ B)
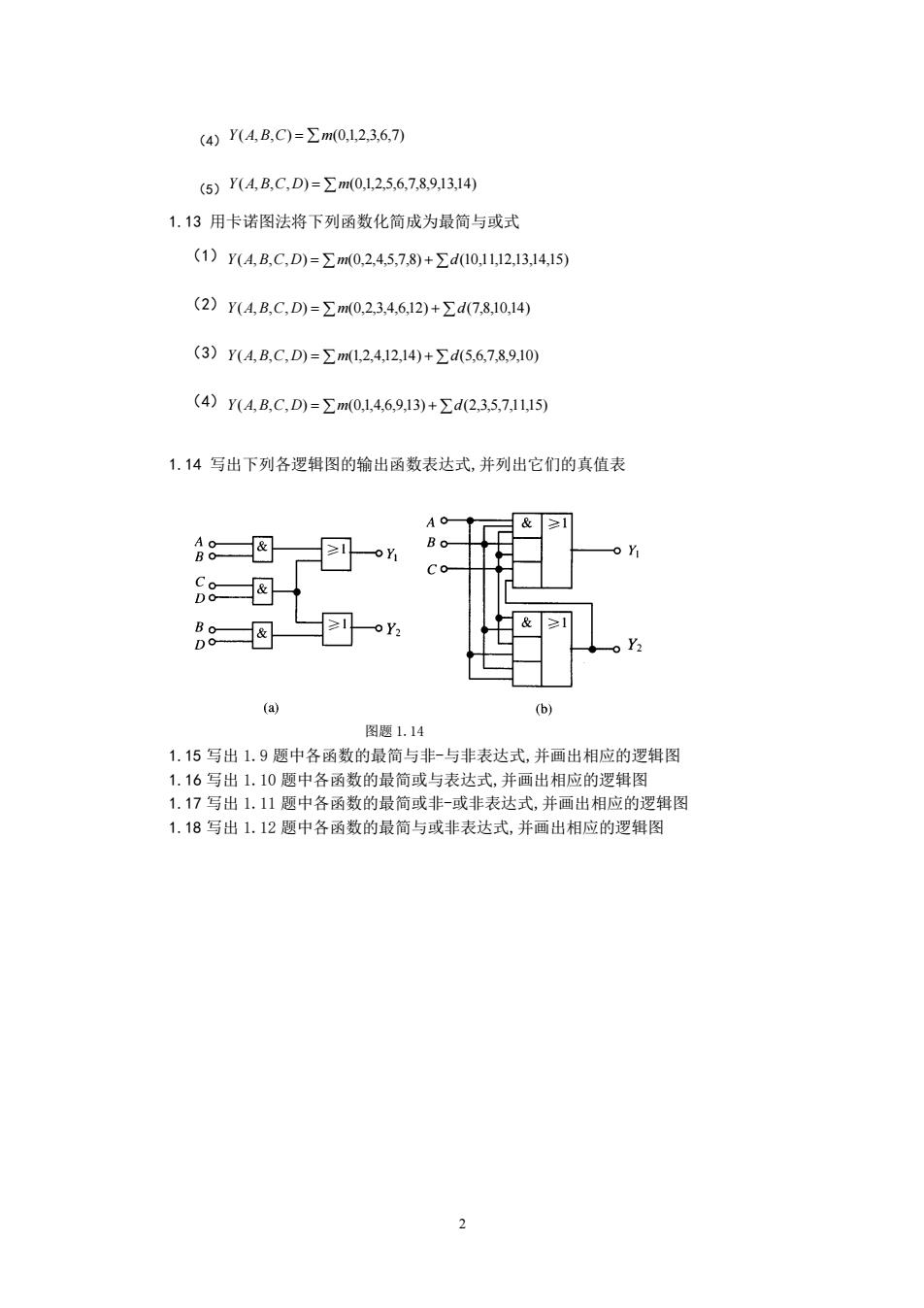
4Y(4B,C)=∑m0,12,36.7) (6)Y4BC,D)=Σm0,125.6,789,134 1.13用卡诺图法将下列函数化简成为最简与或式 (1)Y4,B,C,D)=Σm0,2.457,8)+Σd0,IL2,3,l4,5 (2)Y4,B,C,D)=∑m0,234,612)+∑d7,810,14 (3)YAB,C,D)=∑mL,2,412,14)+Σd5,67,89,10) (4)YA,B,C,D)=∑m0,146,913)+Σd2,35,7115 1,14写出下列各逻辑图的输出函数表达式,并列出它们的真值表 &≥1 48 Bo- 68® 1&≥1 (b) 图题1.14 1.15写出1.9题中各函数的最简与非-与非表达式,并画出相应的逻辑图 1.16写出1.10题中各函数的最简或与表法式.并画出相应的罗辑图 1.17写出1.11题中各函数的最简或非-或非表达式,并画出相应的逻辑图 1.18写出1.12题中各函数的最简与或非表达式,并画出相应的逻辑图
2 (4) Y(A,B,C) = m(0,1,2,3,6,7) (5) Y(A,B,C,D) = m(0,1,2,5,6,7,8,9,13,14) 1.13 用卡诺图法将下列函数化简成为最简与或式 (1) Y(A,B,C,D) = m(0,2,4,5,7,8) + d(10,11,12,13,14,15) (2) Y(A,B,C,D) = m(0,2,3,4,6,12) + d(7,8,10,14) (3) Y(A,B,C,D) = m(1,2,4,12,14) + d(5,6,7,8,9,10) (4) Y(A,B,C,D) = m(0,1,4,6,9,13) + d(2,3,5,7,11,15) 1.14 写出下列各逻辑图的输出函数表达式,并列出它们的真值表 图题 1.14 1.15 写出 1.9 题中各函数的最简与非-与非表达式,并画出相应的逻辑图 1.16 写出 1.10 题中各函数的最简或与表达式,并画出相应的逻辑图 1.17 写出 1.11 题中各函数的最简或非-或非表达式,并画出相应的逻辑图 1.18 写出 1.12 题中各函数的最简与或非表达式,并画出相应的逻辑图