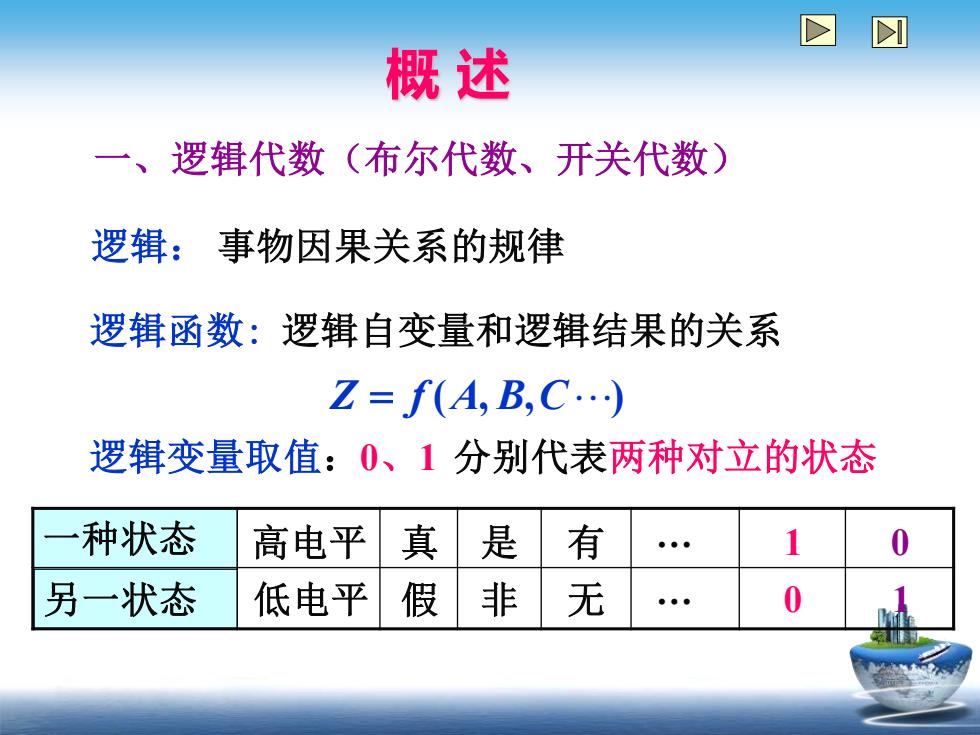
D ☒ 概述 一、逻辑代数(布尔代数、开关代数) 逻辑:事物因果关系的规律 逻辑函数:逻辑自变量和逻辑结果的关系 Z=f(AB,C.) 逻辑变量取值:0、1分别代表两种对立的状态 种状态 高电平 真 是有 另一状态 低电平 假 非无 ●●● 0
一、逻辑代数(布尔代数、开关代数) 逻辑: 事物因果关系的规律 逻辑函数: 逻辑自变量和逻辑结果的关系 Z = f (A, B,C) 逻辑变量取值:0、1 分别代表两种对立的状态 一种状态 另一状态 高电平 低电平 真 假 是 非 有 无 . . 1 0 0 1 概 述

二、二进制数表示法 1.十进制数(Decimal)-逢十进 数码:0~9 位权:10 (12345)10=1×104+2×103+3×102+4×101+5×10° (143.75)0=1×102+4×10'+3×10°+7×10-1+5×10-2 2.二进制数(Binary)-逢二进一 数码:0,1 位权:2 (1011)2=1×23+0×22+1×21+1×2° (101.11)2=1×22+0×2+1×2°+1×21+1×2地
二、二进制数表示法 1. 十进制数(Decimal)- 逢十进一 数码:0 ~ 9 位权: 4 3 2 1 0 = 110 + 210 + 310 + 4 10 + 5 10 2. 二进制数(Binary) - 逢二进一 数码:0 ,1 位权: 2 ( 1011 ) 3 2 1 0 = 1 2 + 0 2 + 1 2 + 1 2 10 ( 12345 ) i 10i 2 2 1 0 1 2 1 10 4 10 3 10 7 10 5 10 − − = + + + + 10 ( 143. 75 ) 2 ( 101.11 ) 2 1 0 1 2 1 2 0 2 1 2 1 2 1 2 − − = + + + +

K I 3.二进制数的缩写形式一八进制数和十六进制数 (1)八进制数(Octal)-逢八进一 数码:0~7 位权:8 (37.41)8=3×8+7×8°+4×81+1×8-2 (2)十六进制数(Hexadecimal)-逢十六进 一 数码:0~9,A(10),B(11),C(12),D(13),E(14),F(15) 位权:16 (2A.7F)16=2×16+10×16°+7×161+15×16-2 任意(N)进制数展开式的普遍形式: D=∑kX k,一第i位的系数N一第i位的权
3. 二进制数的缩写形式 — 八进制数和十六进制数 数码:0 ~ 7 位权: 8 ( 37. 41 ) 1 0 1 2 3 8 7 8 4 8 1 8 − − = + + + (2) 十六进制数 (Hexadecimal) -逢十六进一 数码:0 ~ 9 , A(10) , B(11) , C(12) , D(13) , E(14) , F(15) 位权: i 8 i 16 16 ( 2A. 7F ) 1 0 1 2 2 16 10 16 7 16 15 16 − − = + + + 任意(N)进制数展开式的普遍形式: i D = ki N ki i — 第 i 位的系数 N — 第 i 位的权 (1) 八进制数(Octal)- 逢八进一

4.几种常用进制数之间的转换 ()二十转换:将二进制数按位权展开后相加 (101.11)2=1×22+0×2'+1×2°+1×21+1×2-2 =4+1+0.5+0.25=(5.75)10 (2)十-二转换: 降幂比较法一要求熟记20~210的数值。 20 21 22 23 24 25 26 27 28 29 210 2 4 8 16 32 64 128 256512 1024
4. 几种常用进制数之间的转换 (1) 二-十转换: 将二进制数按位权展开后相加 2 ( 101.11) 2 1 0 1 2 1 2 0 2 1 2 1 2 1 2 − − = + + + + 10 = 4 +1+ 0. 5 + 0. 25 = (5. 75) (2) 十-二转换: 降幂比较法 — 要求熟记 2 0 ∼ 2 10 的数值 。 2 0 2 1 2 2 2 3 2 4 2 5 2 6 2 7 2 8 2 9 2 10 1 2 4 8 16 32 64 128 256 512 1024

I 2)十-二转换:降幂比较法(157)10=(10011101)2 157 -)128 27 28=256>157>27=128 29 25=32>29>24=16 16 24 13 24=16>13>23=8 8 23 5 23=8>5>22=4 -) 4 22 1 2=2>1=2°=1 1 20 0 快速转换法:拆分法 168421 (26)10=16+8+2=24+23+21=(1101
10 2 ( 157 ) = ( 10011101 ) 157 −) 128 29 −) 16 −) 8 5 2 7 2 4 13 快速转换法:拆分法 ( 26 )10 = 16 + 8 + 2 = 2 4 +23 + 21 = ( 1 1 0 1 0 )2 −) 4 1 1 16 8 4 2 1 (2) 十-二转换: 降幂比较法 2 3 2 2 2 0 −) 0 2 256 157 2 128 8 7 = = 2 32 29 2 16 5 4 = = 2 16 13 2 8 4 3 = = 2 8 5 2 4 3 2 = = 2 2 1 2 1 1 0 = = =