
导体系统的电容 ·电容系数 [o]=[p][q] [g]=[p][p]=[B]Lp] 显然,B为p的逆矩阵 B,= M,△是p的行列式,M是P,的代数余子式 。互易介质中:B,=P 。方程组形式: 91=B101+B2p2+…+Bnpm 92=f2191+f22p2+…+B2n0 9n=阝n0+fn202+…+Pnnp. 2011年6月10日星期五 lexu@mail.xidian.edu.cn 2
2011年6月10日星期五 lexu@mail.xidian.edu.cn 12 导体系统的电容 电容系数 显然,β为p的逆矩阵 ,△是p的行列式,Mij是Pij的代数余子式 互易介质中: 方程组形式: ϕ = [][ ][qp ] 1 [ ] [ ] [ ] [ ][ ] q p ϕ βϕ − = = ∆ = ij ij M β 1 11 1 12 2 1 2 21 1 22 2 2 11 2 2 n n n n n n nn n q q q βϕ βϕ βϕ βϕ βϕ βϕ βϕ βϕ βϕ = + ++ = + ++ = + ++ β β ij ji = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
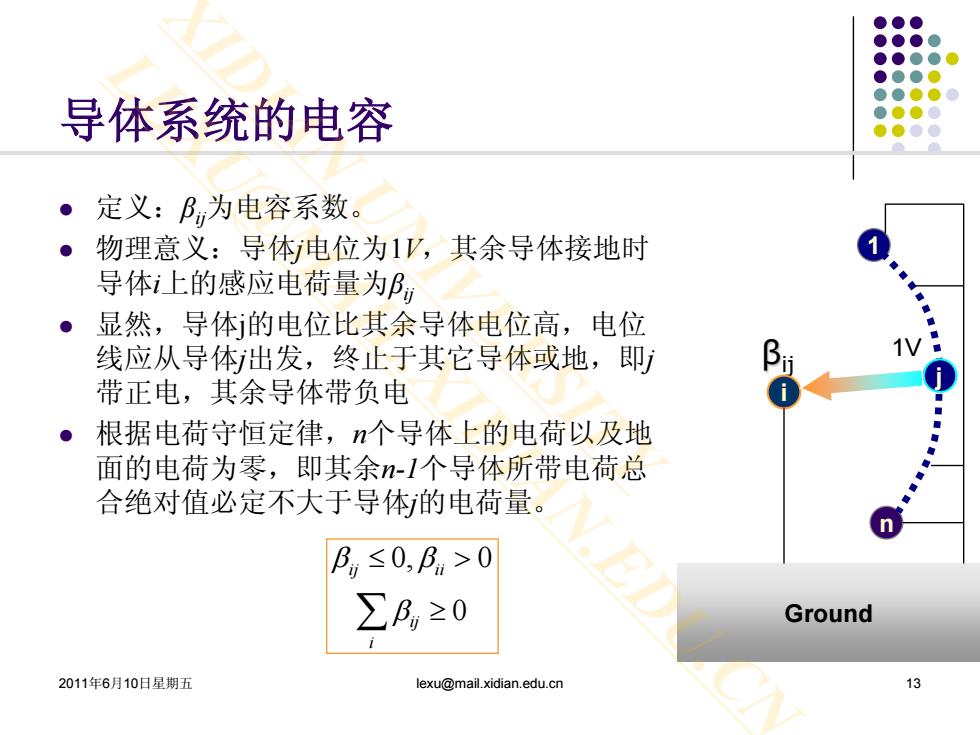
导体系统的电容 ·定义:B为电容系数。 物理意义:导体电位为1V,其余导体接地时 导体i上的感应电荷量为P ●显然,导体j的电位比其余导体电位高,电位 线应从导体出发,终止于其它导体或地,即 带正电,其余导体带负电 根据电荷守恒定律,n个导体上的电荷以及地 面的电荷为零,即其余-1个导体所带电荷总 合绝对值必定不大于导体的电荷量。 B≤0,B>0 ∑B,≥0 Ground 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 13 导体系统的电容 定义:βij为电容系数。 物理意义:导体j电位为1V,其余导体接地时 导体i上的感应电荷量为βij 显然,导体j的电位比其余导体电位高,电位 线应从导体j出发,终止于其它导体或地,即j 带正电,其余导体带负电 根据电荷守恒定律,n个导体上的电荷以及地 面的电荷为零,即其余n-1个导体所带电荷总 合绝对值必定不大于导体j的电荷量。 i n j 1 Ground βij 1V 0, 0 0 ij ii ij i β β β ≤ > ∑ ≥ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

导体系统的电容 。改写: [q]=[B][o] 91=(B,+f2+…+fn)0,-B2(9,-92)-…-fn(9-pn) 9=-B1(02-0)+(B21+B2+…+B2nm2--Pn(02-pn 9n=-fni(pn-0)-fn2(0。-2)-…+(Bn1+fn2+…+Bn)pn 令 C.-2A,C,=-6 j= 91=C11p1+C12(01-p2)+…+C1n(91-pn) 92=C2(02-0)+C22p2+…+C2n(02-p】 2011年6 9n=Cm(pn-p)+C2(pn-p2)+…+CmPn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 14 导体系统的电容 改写: 令 1 11 12 1 1 12 1 2 1 1 2 21 2 1 21 22 2 2 2 2 1 1 2 2 12 ( ) () () ( )( ) ( ) ( )( ) ( ) n n n n nn n n n n n n n nn n q q q β β βϕ βϕ ϕ βϕ ϕ βϕ ϕ β β βϕ βϕ ϕ βϕ ϕ βϕ ϕ β β βϕ = + ++ − − −− − =− − + + + + − − − =− − − − − + + + + [ ] [ ][ ] q = β ϕ 1 , n ii ij ij ij j C C β β = = = − ∑ 1 11 1 12 1 2 1 1 2 21 2 1 22 2 2 2 1 12 2 () () () () ( )( ) n n n n n n n n n nn n qC C C qC C C qC C C ϕ ϕϕ ϕϕ ϕϕ ϕ ϕϕ ϕϕ ϕϕ ϕ = + − ++ − = − + ++ − = − + − ++ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
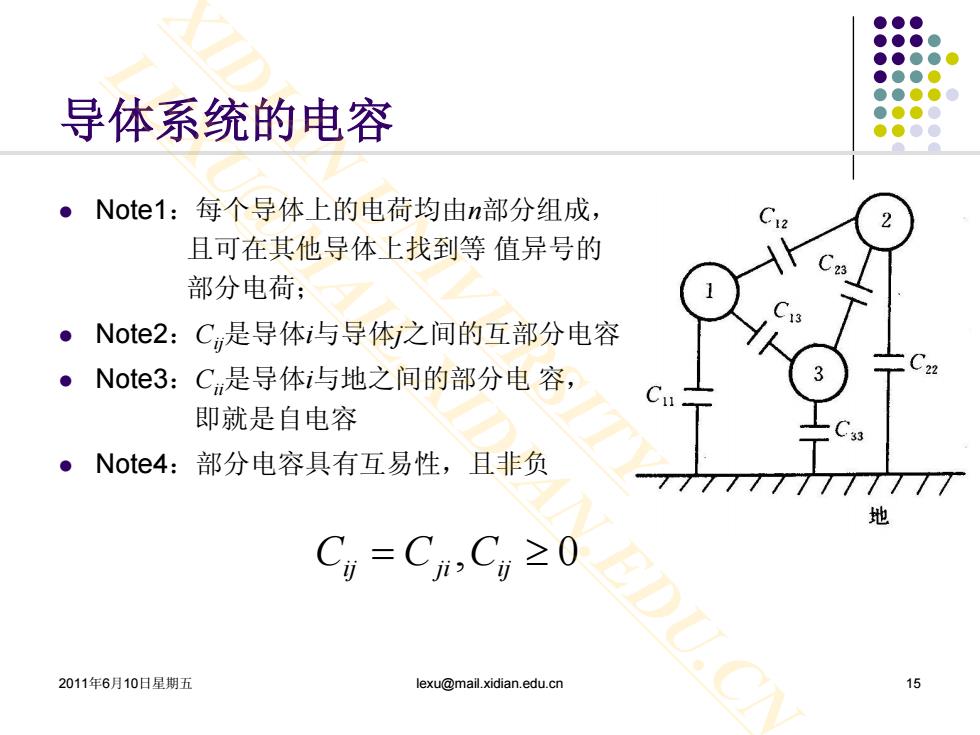
导体系统的电容 ●Note1:每个导体上的电荷均由n部分组成, 且可在其他导体上找到等值异号的 部分电荷: ·Note2:Cm是导体i与导体之间的互部分电容 ·Note3:Cn是导体i与地之间的部分电容, 即就是自电容 。Note4:部分电容具有互易性,且非负 地 C=C,C≥0 2011年6月10日星期五 lexu@mail.xidian.edu.cn
2011年6月10日星期五 lexu@mail.xidian.edu.cn 15 导体系统的电容 Note1:每个导体上的电荷均由n部分组成, 且可在其他导体上找到等 值异号的 部分电荷; Note2:Cij是导体i与导体j之间的互部分电容 Note3:Cii是导体i与地之间的部分电 容, 即就是自电容 Note4:部分电容具有互易性,且非负 , 0 C CC ij ji ij = ≥ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
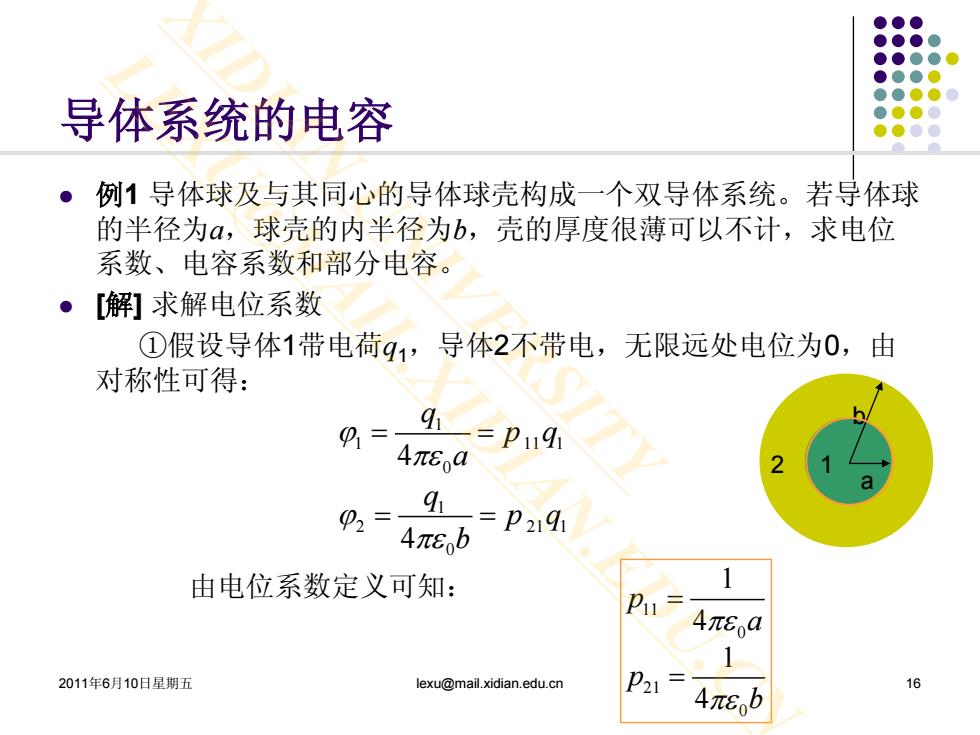
导体系统的电容 例1导体球及与其同心的导体球壳构成一个双导体系统。若导体球 的半径为α,球壳的内半径为b,壳的厚度很薄可以不计,求电位 系数、电容系数和部分电容。 ·[解]求解电位系数 ①假设导体1带电荷91,导体2不带电,无限远处电位为0,由 对称性可得: 91= 941 =p1194 4π6oa ⊙ 91 =p2191 4π6b 由电位系数定义可知: 1 P11= 4πeoa 1 2011年6月10日星期五 lexu@mail.xidian.edu.cn P21= 4πEb
2011年6月10日星期五 lexu@mail.xidian.edu.cn 16 导体系统的电容 例1 导体球及与其同心的导体球壳构成一个双导体系统。若导体球 的半径为a,球壳的内半径为b,壳的厚度很薄可以不计,求电位 系数、电容系数和部分电容。 [解] 求解电位系数 ①假设导体1带电荷q1,导体2不带电,无限远处电位为0,由 对称性可得: 由电位系数定义可知: 2 1 a 1 b 1 11 1 0 1 2 21 1 0 4 4 q p q a q p q b ϕ πε ϕ πε = = = = 11 0 21 0 1 4 1 4 p a p b πε πε = = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN