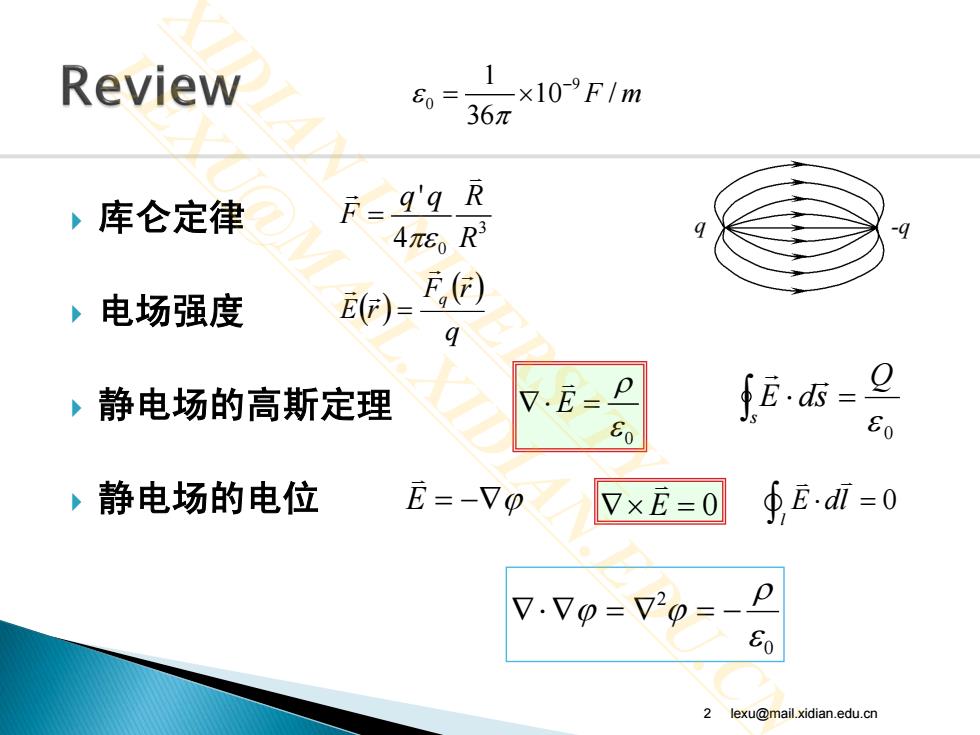
Review 60 10FIm 36元 ,库仑定律 F=9'9R 4nEo R 9 ,电场强度 邱)E⊙ 9 ,静电场的高斯定理 V.E-P LE.ds-2 ⊙ 0 ,静电场的电位 E=-7p 7xE=0 ∮E.dl=0 V.Vp=70=- 80 2 lexu@mail.xidian.edu.cn
库仑定律 电场强度 静电场的高斯定理 静电场的电位 2 lexu@mail.xidian.edu.cn 3 0 ' 4 qq R F πε R = 9 0 1 10 / 36 ε F m π − = × ( ) ( ) q rF rE q = 0 ε Q sdE s =⋅ ∫ 0 E ρ ε ∇⋅ = ∇× = E 0 0 l E dl ⋅ = ∫ E = −∇ϕ 0 2 ε ρ ϕϕ −=∇=∇⋅∇ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

UNIVERSITY 第4讲静电场(II) 电偶极子 介质极化 束缚电荷 介质高斯定理 介质中的场方程 静电场边界条件 电位微分方程 3lexu@mail.xidian.edu.cn
电偶极子 介质极化 束缚电荷 介质高斯定理 介质中的场方程 静电场边界条件 电位微分方程 3 lexu@mail.xidian.edu.cn XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

电偶极子 ,电偶极子是由间距很小的一对等值异号的点电荷所构成的 一种电荷分布 ,由迭加原理,处产生的电位为: p(F)= 9 4π0 2 ,因为r>>1,故可将上式展开, 略去一些次要项,可得: 11 r.I ≈-(1+ p)= p.r 4π8r3 2 p=gl 称为电偶极子的矩e简称电偶极矩
电偶极子是由间距很小的一对等值异号的点电荷所构成的 一种电荷分布 由迭加原理,r处产生的电位为: 因为 ,故可将上式展开, 略去一些次要项,可得: 4 lexu@mail.xidian.edu.cn ) 2 1 2 1 ( 4 )( 0 l r l r q r + − − = πε ϕ >> lr 2 1 1 (1 ) 2 2 r l l r r r ⋅ ≈ + − 2 1 1 (1 ) 2 2 r l l r r r ⋅ ≈ − + ( ) 3 4 0 r rp r πε ϕ ⋅ = lqp = 称为电偶极子的矩,简称电偶极矩 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

电偶极子 电偶极矩表示电偶极子的大小和空间取向 。它定义为电荷q乘以有向距离1 ,电偶极子的电场 。电场强度与电位的关系:E=-V0 片=v,D=g是常矢 E()=-( E(F)=-Y p.F 4πEr1 4πEor3 V(4.B)=Bx(Vx)+(B.V)4 (a.V)B=4, aB aB B Ay dy +A×(V×B)+(A.V)B +A. 0z )= 1 3(p. 30,-币 4π6L r 4π8r 六3 5 lexu@mail.xidian.edu.cn
◦ 电偶极矩表示电偶极子的大小和空间取向 ◦ 它定义为电荷q乘以有向距离 电偶极子的电场 ◦ 电场强度与电位的关系: 5 lexu@mail.xidian.edu.cn l E = −∇ϕ ( ) 3 0 4 p r E r πε r ⋅ = −∇ 3 1 ˆ , r p ql r r = −∇ = 是常矢 ( ) ( ) 3 0 4 r Er p πε r = − ⋅∇ ( ) ( ) ( ) − ⋅ = − ⋅ = pr r rp rr p r rrp rE 3 2 0 5 3 0 3 4 3 1 4 1 πε πε ( ) ( )( ) ( )( ) AB B A B A A B AB ∇ ⋅ = × ∇× + ⋅∇ + × ∇× + ⋅∇ ( ) xyz BBB A BA A A xyz ∂∂∂ ⋅∇ = + + ∂∂∂ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

电偶极子 ,球坐标系下电偶极子的电场强度: 。球坐标系下: p=a:p=p(a,cose-do sin 0) (a,2cos0+asin9)) 4π8r ,Note1:电偶极子的电位和电场分别与r2和r3成反比;而 点电荷的电位和电场分别与r和2成反比;这 是由于电偶极子的正负电荷在远 场的贡献有一部分相互抵消。 ,Note2:电偶极子的场分布具有轴对称性 6 lexu@mail.xidian.edu.cn
球坐标系下电偶极子的电场强度: ◦ 球坐标系下: Note1:电偶极子的电位和电场分别与 和 成反比;而 点电荷的电位和电场分别与 和 成反比;这 是由于电偶极子的正负电荷在远 场的贡献有一部分相互抵消。 Note2:电偶极子的场分布具有轴对称性 6 lexu@mail.xidian.edu.cn ( θθ ) θ cos aappap sin z r == − ( θθ ) πε θ 2cos sin 4 3 0 a a r p E r = + 2 r 3 r r 2 r XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN