
电磁场与电磁波基础 主讲:徐乐 商安后子州找大是
电磁场与电磁波基础 主讲:徐乐
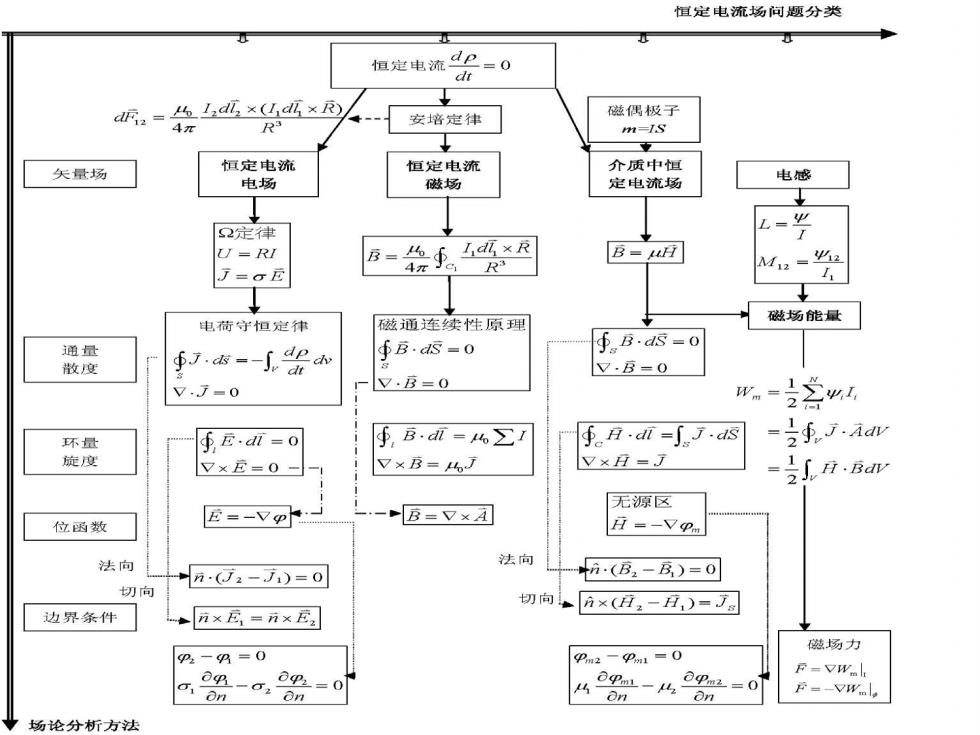
恒定电流场问题分类 恒定电流dP=0 dt cd2=么Id互x山cd× 磁偶极子 4π R 安培定律 m-IS 矢量场 恒定电流 恒定电流 介质中恒 电场 磁场 定电流场 电感 2定律 U=RI B=会手%R B- 了= AL2=2 磁通连续性原理 磁场能量 电荷守恒定律 通量 ∮=盼 ∮B.S=0 5BS=0 散度 V.B=0 V.7=0 V.B=0 m=空如以 环量 ∮E,dn=0 5,B·n=∑ fAdi=∫Jcd因 3手ia = 旋度 V×它=0 V×B=,J V×H=万 -iS A.Bdv 无源区 位函数 E=-Vp B=V×A H=-Vpn 法向 法向 n·(J2-J1)=0 n(B2-)=0 切向 切向方×(H2-A,)=J8 边界条件 ◆n×E=n×E 磁场力 P:-9=0 Pm2-P =0 a=0 0Pm2=0 F-VW F=-VWilo 场论分析方法
lexu@mail.xidian.edu.cn 2
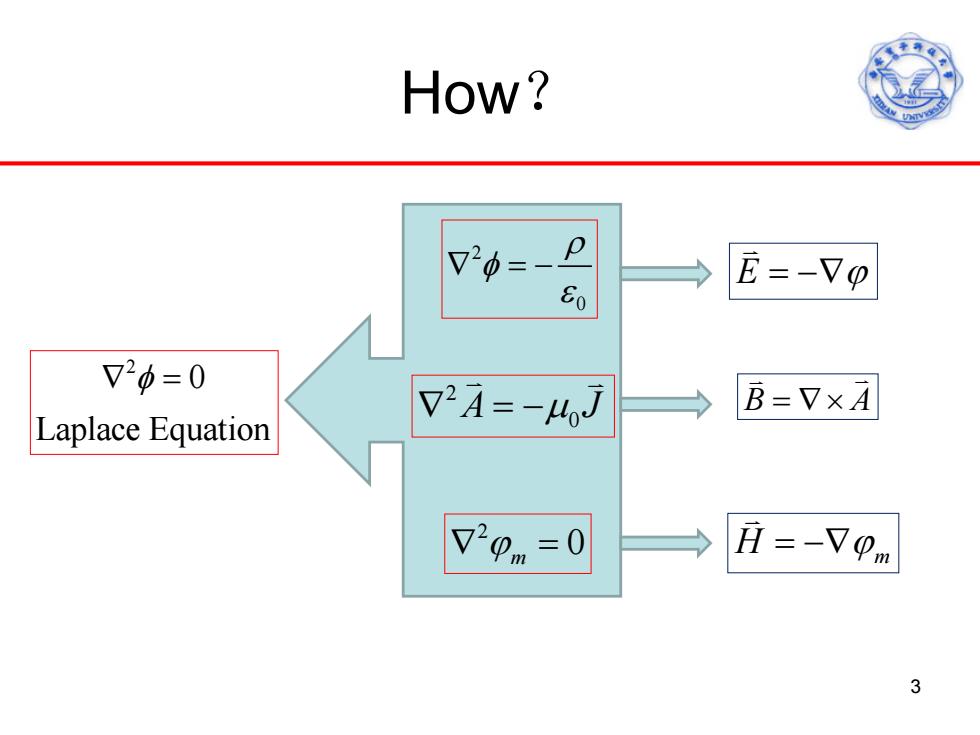
How? E=-Vo 7b=0 V24=-MoJ B=V×A Laplace Equation =0 H=-Vm 3
How? 3 E = −∇ϕ 2 0 ρ φ ε ∇ =− B A =∇× 2 ∇ =− A J µ0 H = −∇ϕ m 2 0 ∇ = ϕ m 2 0 Laplace Equation ∇ = φ
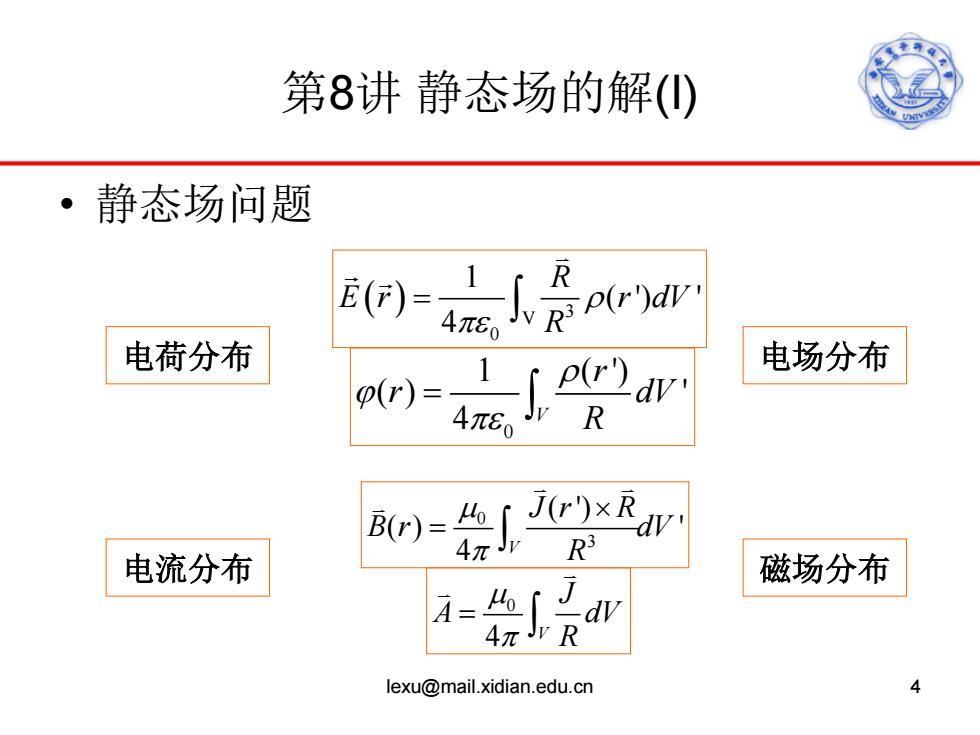
第8讲静态场的解() 、静态场问题 电荷分布 s e(rdv' 电场分布 p()= 4π80 Jv R R3 电流分布 =∫*A 磁场分布 小-会质 lexu@mail.xidian.edu.cn 4
第8讲 静态场的解(I) • 静态场问题 lexu@mail.xidian.edu.cn 4 ( ) 3 V 0 1 ( ') ' 4 R E r r dV R ρ πε = ∫ 0 1 ( ') ( ) ' 4 V r r dV R ρ ϕ πε = ∫ 0 3 ( ') ( ) ' 4 V Jr R B r dV R µ π × = ∫ 0 4 V J A dV R µ π = ∫ 电荷分布 电场分布 电流分布 磁场分布

第8讲静态场的解() 、 静电场问题可分为两类: 一一类是前面讨论的己知源分布求解场的分布型问题; 一一类是由场量所满足的支配方程以及场量在边界上的 已知条件来求解场的边值型问题。 ·边值型问题的空间场分布可化为求解给定边界条件 下位函数的拉普拉斯方程或泊松方程,即求解边值 问题。 ·拉普拉斯方程是二阶偏微分方程,可用解析法、数 值计算法、实验模拟法及图解法等方法求解。 lexu@mail.xidian.edu.cn 5
第8讲 静态场的解(I) • 静电场问题可分为两类: – 一类是前面讨论的已知源分布求解场的分布型问题; – 一类是由场量所满足的支配方程以及场量在边界上的 已知条件来求解场的边值型问题。 • 边值型问题的空间场分布可化为求解给定边界条件 下位函数的拉普拉斯方程或泊松方程,即求解边值 问题。 • 拉普拉斯方程是二阶偏微分方程,可用解析法、数 值计算法、实验模拟法及图解法等方法求解。 lexu@mail.xidian.edu.cn 5