
>三、多抽样率信号处理的内容 >1、信号的抽取(Decimation); >2、信号的插值(Interpolation); >3、抽取与插值的实现、多相结构、多抽样率系统; >4、两通道滤波器组,分析与综合; >5、多抽样率信号处理的应用
三、多抽样率信号处理的内容 1、信号的抽取(Decimation); 2、信号的插值(Interpolation); 3、抽取与插值的实现、多相结构、多抽样率系统; 4、两通道滤波器组,分析与综合; 5、多抽样率信号处理的应用

5.2信号的抽取 >抽取: f,→f/M 抽样频率减少M倍 x(n) y(n) IM Down-Sampler 最简单的方法是将x(n)中每M个点中抽取一个, 次组成一个新的序列,即: y(n)=x(Mn)
5.2 信号的抽取 抽取: f s f s / M 抽样频率减少M倍 ↓M x(n) y(n) Down-Sampler 最简单的方法是将 中每M个点中抽取一个,一 次组成一个新的序列,即: x(n) y(n) x(Mn) n ~

y(n)=x(Mn) n三-00入~00 M=3 y(0)=x(0) y1)=x(3) y(2)=x(6) y(3)=x(9) 舍弃了(M-1)M部分的数据
y(n) x(Mn) n ~ M 3 y(0) x(0) y(1) x(3) y(2) x(6) y(3) x(9) 舍弃了(M-1)/M部分的数据 . . .
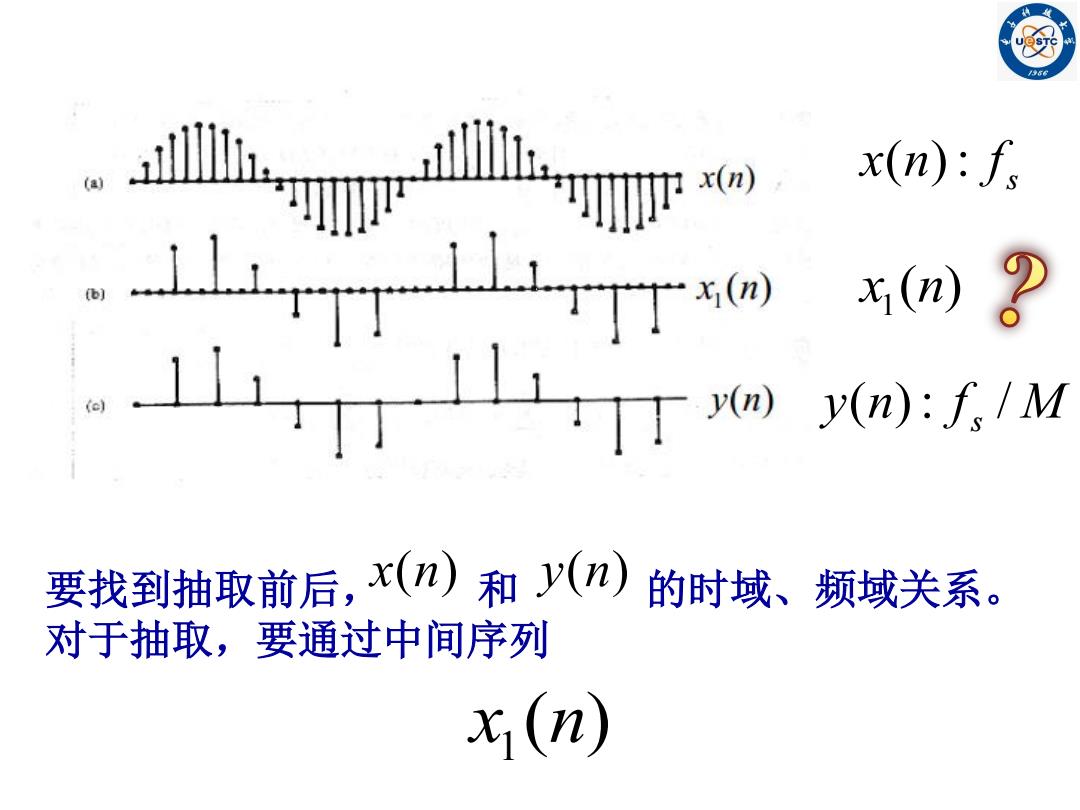
x(n) x(n):f x0) x(n) y(n):f./M 要找到抽取前后,x(n)和y(n): 的时域、频域关系。 对于抽取,要通过中间序列 x,(n)
s x(n): f ( ) x1 n y(n): f s / M 要找到抽取前后, 和 的时域、频域关系。 对于抽取,要通过中间序列 x(n) y(n) ( ) x1 n

>现证 Y@)- e k=0 明如右 M-1 的关系: k-0 >证明: y(n)=x(Mn) 两者的抽 样频率不 Y(z)=∑y0n)z"=∑x(Mm)z" 一样,使 用的点数 n=-00 n=-o0 不一样 Mn=m,Y(=)=>x(m)zmIM =X(2M) m=-00
现证 明如右 的关系: 10 ( 2 )/ 10 1( ) 1 ( ) ( ) 1 ( ) Mk j j k M Mk M k X e M Y e X z W M Y z 证明: y(n) x(Mn) n n n n Y(z) y(n)z x(Mn)z 两者的抽 样频率不 一样,使 用的点数 不一样 m m M M Mn m,Y(z) x(m)z X (z ) / 1/