
n=0,±M,±2M,…, 其它 x(n)的抽样率仍是f y(n)的抽样率是f,/M 现在的任务是: 了1.要找到x(n)和x(n)之间时域和频域的关系 了2.要找到x(n)和yn之间时域和频域的关系 了3.要找到y(n)和x(n)之间时域和频域的关系
令: 的抽样率仍是 的抽样率是 现在的任务是: 1.要找到 和 之间时域和频域的关系 2.要找到 和 之间时域和频域的关系 3.要找到 和 之间时域和频域的关系 1 ( ) ( ) 0 x n x n n M M 0, , 2 , , 其它 1 x n( ) 1 x n( ) s f y n( ) y n( ) y n( )/ s f M 1 x n( ) x n( ) x n( )

y(n)=x(Mn )=x(Mn) Y(e)=∑x(Mn)z"=∑x(n) -nlM n=-o∞ n=-∞ 正确 Y()=X(2M) 关键是x,(n)和x(n)之间的关系: 尽管二者的 抽样频率不 叉 p(n)=∑dn-M0 一样,但后 i=-o∞ 者在和前者 为一脉冲序列,其抽样频率也为∫, 不一样的地 方全为零
关键是 和 之间的关系: 令 为一脉冲序列,其抽样频率也为 1 y n x Mn x Mn ( ) ( ) ( ) / 1 1 ( ) ( ) ( ) n n M n n Y z x Mn z x n z ( ) ( ) i p n n Mi 1 x n( ) x n( ) s f 尽管二者的 抽样频率不 一样,但后 者在和前者 不一样的地 方全为零 正确 1 1 ( ) ( ) M Y z X z

x(n)=x(n)p(n) A: M-1 WM=eJ2π1M k=0 周期序列展为傅里叶级数 X,(z)=∑x(n)p(n)z" n=-00 空 M-1 1=-00 k=0 1 M m:m9) k=0 n=-o0
1 x n x n p n ( ) ( ) ( ) 1 0 1 ( ) M kn M k p n W M 周期序列展为傅里叶级数 j M 2 / W e M 1 0 1 ( ) M kn n M n k x n W z M 1 0 1 ( )( ) M k n M k n x n zW M 1 ( ) ( ) ( ) n n X z x n p n z

所以: te-是:时, k=0 又因为: Y(z)=X (2M) 最后: ye)-2xew) MK-0 信号抽 z=elo 取前后 频域的 关系 M-1 rea=7∑xeo-awm)
所以: 又因为: 最后: 1 1 0 1 ( ) ( ) M kM k X z X zW M 1/ 1 ( ) ( ) M Y z X z 1 1 0 1 ( ) ( ) M M k k Y z X z W M j z e 信号抽 取前后 频域的 关系
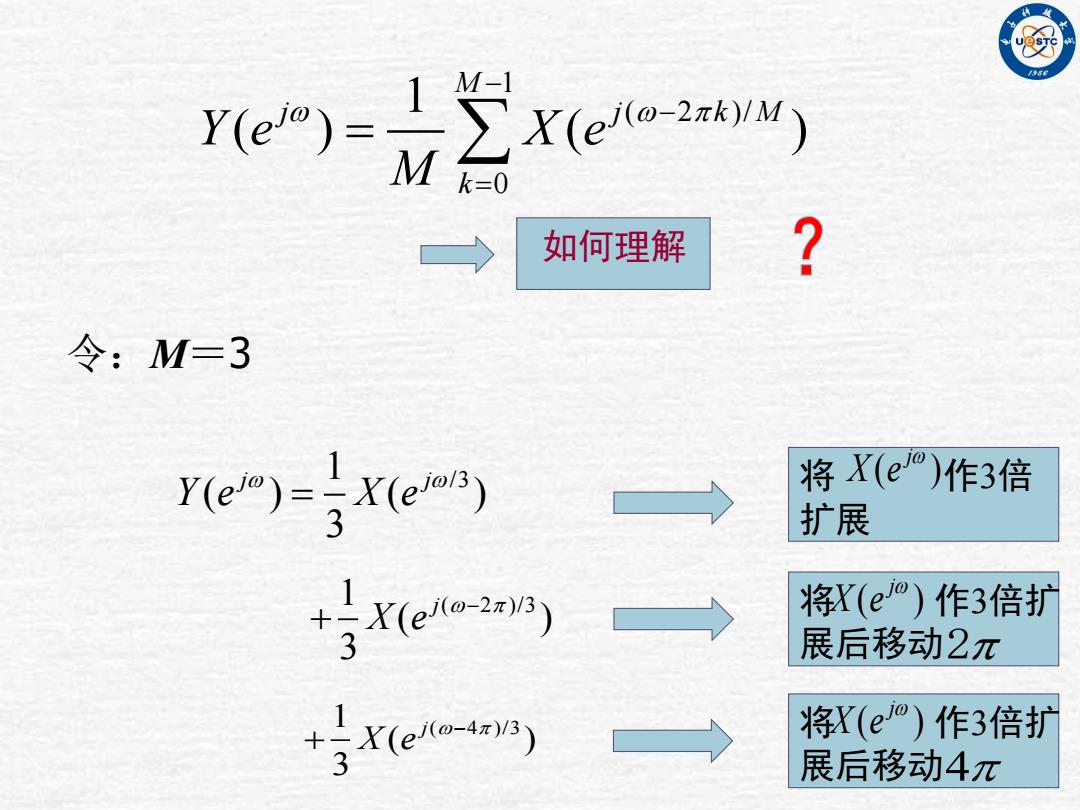
e号艺xeaw k=0 如何理解 令:M=3 e)号e 将X(e)作3倍 扩展 +号e) 将X(e)作3倍扩 展后移动2π +re-an) 二I 将X(eo)作3倍扩 展后移动4π
令:M=3 1 ( 2 )/ 0 1 ( ) ( ) M j j k M k Y e X e M 如何理解 1 / 3 ( ) ( ) 3 j j Y e X e 1 ( 2 )/3 ( ) 3 j X e 1 ( 4 )/3 ( ) 3 j X e 将 作3倍 扩展 将 作3倍扩 展后移动 ( ) j X e ( ) j X e 2 将 作3倍扩 展后移动 ( ) j X e 4