
电路学习辅导 第十五章动态电路的复频域求解 第十五章动态电路的复频域求解 一本章要求 1.握拉普拉斯变换,拉普拉斯反变换(部分分式展开法)。 2.握电路定律及各电路元件的复频域形式。 3.握运算阻抗、运算导纳等概念。 4.电路的复频域分析法。 二内容提要 1.时间函数f)的拉普拉斯变换 F(s)==[f(e-"di (15-1) F(s)为f0)得像函数,f0为F(s)的原函数,s=c+jo为复频率。 2.拉普拉斯变换的性质 a)线性性质L[a)+b时,(】=aE(s)+b5,(s) (15-2) b)延迟性质ft-to)e(t-t】=eF(s) (15-3) 。微分性质0]=F)-f0.) (15-4) d d)积分性质fu)d=F(s)/s (15-5) 3.普拉斯反变换,部分分式展开法 当F付=因.么,产+么++5+么为假分式时,则利用长除法先转化 D(s)ans"+as"+.+as+ao 为整式加真分式,再求f)。 当F(S)为真分式时,n>m。 1)D(S)0有P,P2P个实单根时,则 F=2年4=s-n)s=n或A=D 后s-Pk D(s) D(P) 则f)=∑Aeu (15-6) =l 2)D(s)-0有一对共轭根P1=a+j0,P2=a-j0,则 18
电路学习辅导 第十五章 动态电路的复频域求解 118 第十五章 动态电路的复频域求解 一 本章要求 1. 握拉普拉斯变换,拉普拉斯反变换(部分分式展开法)。 2. 握电路定律及各电路元件的复频域形式。 3. 握运算阻抗、运算导纳等概念。 4. 电路的复频域分析法。 二 内容提要 1. 时间函数 f(t)的拉普拉斯变换 F s L f t f t e dt st − − = = 0 ( ) [ ( )] ( ) (15-1) F(s)为 f(t)得像函数,f(t)为 F(s)的原函数, s = + j 为复频率。 2.拉普拉斯变换的性质 a) 线性性质 [ ( ) ( )] ( ) ( ) 1 2 1 2 L af t + bf t = aF s + bF s (15-2) b) 延迟性质 [ ( ) ( )] ( ) 0 0 0 L f t t t t e F s −st − − = (15-3) c) 微分性质 ] ( ) (0 ) ( ) [ = − − sF s f dt df t L (15-4) d) 积分性质 L f t dt F s s t [ ( ) ( )/ 0 = − (15-5) 3. 普拉斯反变换,部分分式展开法 当 1 0 1 1 0 1 1 ( ) ( ) ( ) a s a s a s a b s b s b s b D s N s F s n n n n m m m m + + + + + + + + = = − − − 为假分式时,则利用长除法先转化 为整式加真分式,再求 f(t)。 当 F(s)为真分式时,n>m。 1〉 D(s)=0 有 p1 p2 pk , 个实单根时,则 k k k n k k k s p D s N s A s p s p A F s = − = − = = ]| ( ) ( ) ( ) , [( ) 1 或 ( ) ( ) k k k D p N p A = 则 = = n k p t k k f t A e 1 ( ) (15-6) 2〉 D(s)=0 有一对共轭根 p1 = + j, p2 = − j ,则
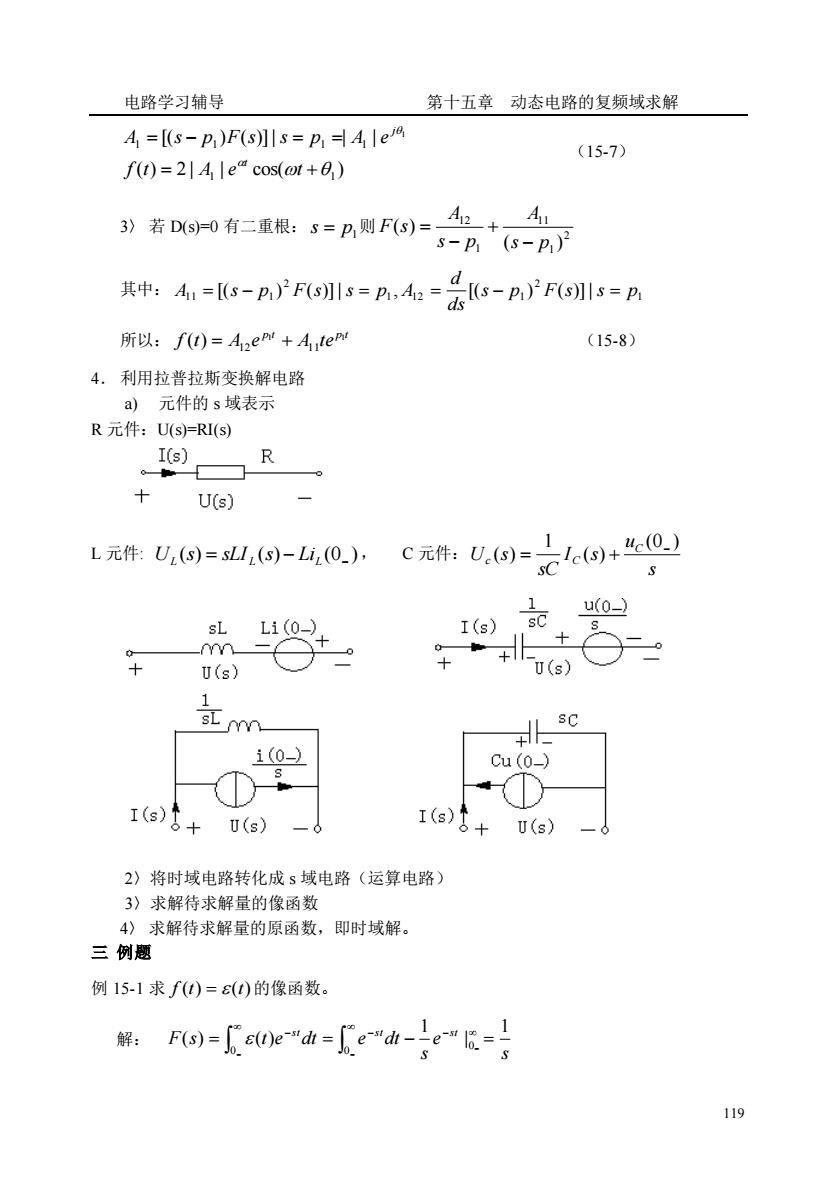
电路学习辅导 第十五章动态电路的复频域求解 A=s-p)F(s川s=p,AIe (15-7) f)=2|4le“cos(om+0) 》若时有=A圆FO-为石A 其中:A1=[s-P)产Fss=P,42= 孟s-aNFo:=n 所以:f(u)=Aem+A,lePm (15-8) 4.利用拉普拉斯变换解电路 a)元件的s域表示 R元件:U(s=RI(S) 1(Gs)R U(s) L元#份=@-山0:c元指o)=之:o+0 sLL1(0-) sC u(0 U(s) U(s) 1 sC 1(0-) Cu(0-) ①D I(s)+U(s) I(s)+U(s) 2)将时域电路转化成s域电路(运算电路) 3)求解待求解量的像函数 4)求解待求解量的原函数,即时域解。 三例题 例15-1求f()=()的像函数。 解,F=e0eh-eh-e"R-号 19
电路学习辅导 第十五章 动态电路的复频域求解 119 ( ) 2 | | cos( ) [( ) ( )]| | | 1 1 1 1 1 1 1 = + = − = = f t A e t A s p F s s p A e t j (15-7) 3〉 若 D(s)=0 有二重根: p1 s = 则 2 1 11 1 12 ( ) ( ) s p A s p A F s − + − = 其中: 1 2 1 1 2 1 2 1 1 1 [( ) ( )]| , [(s p ) F(s)]| s p ds d A = s − p F s s = p A = − = 所以: p t p t f t A e A te 1 1 12 11 ( ) = + (15-8) 4. 利用拉普拉斯变换解电路 a) 元件的 s 域表示 R 元件:U(s)=RI(s) L 元件: ( ) ( ) (0 ) L = L − LiL − U s sLI s , C 元件: s u I s sC U s C c C (0 ) ( ) 1 ( ) − = + 2〉将时域电路转化成 s 域电路(运算电路) 3〉求解待求解量的像函数 4〉 求解待求解量的原函数,即时域解。 三 例题 例 15-1 求 f (t) = (t) 的像函数。 解: s e s F s t e dt e dt st st st 1 | 1 ( ) ( ) 0 0 0 = = − = − − − − − −

电路学习辅导 第十五章动态电路的复频域求解 例15-2已知:f0)如图15-1所示,求Fs)。 木f) 解: f)=2s(0-1-2)-1-4) .F)=2= 02 图15-1例152图 例15-3已知:Fs)=5+1s+2 s+4 ,求原函数f): 解: A3 8+4 S+4 4=e。5w+Ws+2hws+i+2-2 A2=(s+1)F(s)川=-1=-3 A=(s+2)F(s)l-2=1 F6)=23 55+its+2f0=2-3e+e 5+2 例154已知:Fs)=子+25+2'求原函数0: 解 s2+2s+2=0→p1=-1+jL,P2=-1-j1 L-45 A=(s+1-F(儿-n='2 ∴fu0=V2ecos1-45) 例15-5已知F(s)= 7s+8 (6+(5+2少,求原函数0。 解: A31 A1=sF(s)lo=2,A2=(s+1)F(s)l-1=-1 4=2s+2yFsL=-l4=g+2FeL=-3 ∴f0=2-e'-e2-3e-2 120
电路学习辅导 第十五章 动态电路的复频域求解 120 例 15-2 已知:f(t)如图 15-1 所示,求 F(s)。 解: (2 ) 2 1 ( ) ( ) 2 ( ) ( 2) ( 4) 2 4 2 4 s s s s e e s s e s e s F s f t t t t − − − − = − − = − − = − − − − 图 15-1 例 15-2 图 例 15-3 已知: ( 1)( 2) 4 ( ) + + + = s s s s F s ,求原函数 f(t)。 解: t t s s s s s f t e e s s s F s A s F s A s F s s s s s s s s A sF s s s A s A s A F s 2 3 2 2 1 1 0 0 0 1 2 3 , ( ) 2 3 2 1 1 2 3 ( ) ( 2) ( ) | 1 ( 1) ( ) | 3 | 2 ( 1)( 2) 4 | ( 1)( 2) 4 ( ) | 1 2 ( ) − − =− =− = = = = − + + + + = − = + = = + = − = + + + = + + + = = + + + = + 例 15-4 已知: 2 2 2 ( ) 2 + + + = s s s F s ,求原函数 f(t)。 解 ( 0 2 cos( 45 ) 45 2 2 ( 1 ) ( ) | 2 2 0 1 1, 1 1 1 1 1 1 2 2 t o o s j f t e t A s j F s s s p j p j = − = + − = − + + = = − + = − − − =− + 例 15-5 已知 2 ( 1)( 2) 7 8 ( ) + + + = s s s s F s ,求原函数 f(t)。 解: t t t s s s s f t e e t e s F s A s F s ds d A A sF s A s F s s A s A s A s A F s 2 2 2 2 2 31 2 32 1 0 2 1 2 1 2 32 31 ( ) 2 3 [( 2) ( )]| 1, ( 2) ( ) | 3 ( ) | 2, ( 1) ( ) | 1 1 2 ( 2) ( ) − − − =− =− = =− = − − − = + = − = + = − = = = + = − + + + + + = +

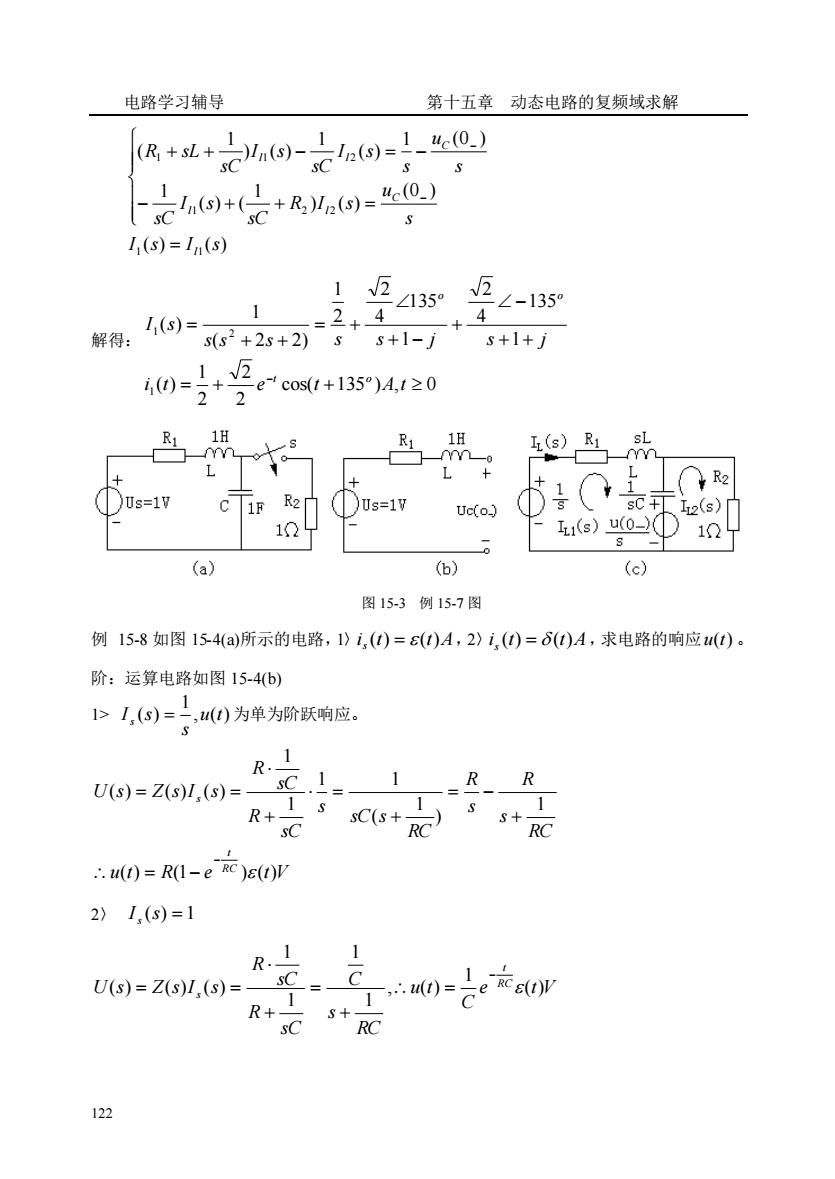
电路学习辅导 第十五章动态电路的复频域求解 例15-6电路如图15-2(a)所示,电路己达到稳态,0时,s打开,已知: B=10AR=R=402,L=4H,C=0.01F,求:s打开后的c。 解:1)0等效电路如图15-2(b)所示,则 R 40.)=R+R,=5A4.0.)=R,0.)=40x50=20r 2)t≥0.后,运算电路如图15-2(c) 其中:U,()=W,R1=0×40=40 由: -U@+R1,+.0-.0.)+24()+“e0)=0 U.)+4,0.)-e0)400+4x5-200 1(s) 5s+50 R++记 40+4s+001s 1 52+105+25 KVLUc(s)= 58+50+200 =0.0l×g2+105+25+5 =400-500200 ss+5)72s+5 4c(0=400-500re-200e5y,1≥0 R2 t0)R2 ++ 4 5S) D (a) (b) ( 图15-2例15-6图 例15-7如图15-3(a)所示的电路原来已处于稳态,0时,s闭合,用运算法求s和上后 的(t)。 解:1)0_等效电路如图15-3(b)所示,则 i,(0)=0,4c(0.)=U.=1W b)运算电路如图15-3(©),列回路方程 121
电路学习辅导 第十五章 动态电路的复频域求解 121 例 15-6 电路如图 15-2(a)所示,电路已达到稳态,t=0 时,s 打开,已知: Is =10A,R1 = R2 = 40,L = 4H,C = 0.01F ,求:s 打开后的 C u 。 解:1〉 − 0 等效电路如图 15-2 (b)所示,则 I A u R i V R R R i L (0 ) s 5 , C (0 ) 2 L (0 ) 40 50 200 1 2 1 = = = = + − = − − 2〉 0+ t 后,运算电路如图 15-2(c) 其中: s Us s L I sR L 400 ( ) [ ] [10 40] = 1 = = 由: KVL ( ) 400 500 200 , 0 5 200 ( 5) 400 500 200 10 25 5 50 0.01 (0 ) 1 ( ) 1 ( ) 10 25 5 50 0.01 1 40 4 200 4 5 400 1 (0 ) ( ) (0 ) ( ) 0 (0 ) ( ) 1 ( ) ( ) ( ) (0 ) 5 5 2 2 2 1 1 = − − + − + = − + + + + = + = + + + = + + + − = + + + − = − + + − + + = − − − − − − − u t t e e V t s s s s s s s s s u I s sC U s s s s s s s s sC R sL s u U s Li I s s u I s sC U s R I s sLI s Li t t C C C L C s L L C s L L L L 图 15-2 例 15-6 图 例 15-7 如图 15-3 (a) 所示的电路原来已处于稳态,t=0 时,s 闭合,用运算法求 s 和上后 的 ( ) 1 i t 。 解:1〉 − 0 等效电路如图 15-3 (b)所示,则 i 1 (0− ) = 0,uC (0− ) = Us =1V b) 运算电路如图 15-3 (c),列回路方程
电路学习辅导 第十五章动态电路的复频域求解 R+L+2-a=}40 sC 2o*定+民国=40 I1(s)=1n(s) 1 1 35 2∠-135 解得: 1(s)= =2+4 (52+2s+2)3s+1-j 3+1+j 2 +2ecos1+135911≥0 I(s)R1 L )Us=1V 1F R2 Us=1V SC+ Uc(o) 、2(s) 12 )0-①1n (a) (6) (c) 图15-3例15-7图 例15-8如图154a)所示的电路,1Di,()=c(1)A,2)i,(0=6)A,求电路的响应()。 阶:运算电路如图15-4(b) L()-0为单为跃南位。 R.、1 U(s)=Z(s)1,(s)= sC 1 1 R R R*C 1 RC u0=Rl-e元)so)p 2)1(s)=1 R 1 U(s)=Z(s)I,(s)= R+ s+ sC RC 122
电路学习辅导 第十五章 动态电路的复频域求解 122 ( ) ( ) (0 ) ) ( ) 1 ( ) ( 1 1 (0 ) ( ) 1 ) ( ) 1 ( 1 1 1 2 2 1 1 2 I s I s s u R I s sC I s sC s u s I s sC I s sC R sL l C l l C l l = − + + = + + − = − − − 解得: cos( 135 ) , 0 2 2 2 1 ( ) 1 135 4 2 1 135 4 2 2 1 ( 2 2) 1 ( ) 1 1 2 = + + + + − + + − = + + + = − i t e t A t s s s s s j s j I s t o o o 图 15-3 例 15-7 图 例 15-8 如图 15-4(a)所示的电路,1〉 i s (t) = (t)A,2〉 i s (t) = (t)A ,求电路的响应 u(t) 。 阶:运算电路如图 15-4(b) 1> , ( ) 1 ( ) u t s I s s = 为单为阶跃响应。 u t R e t V RC s R s R RC sC s s sC R sC R U s Z s I s RC t s ( ) (1 ) ( ) 1 ) 1 ( 1 1 1 1 ( ) ( ) ( ) − = − + = − + = + = = 2〉 I s (s) = 1 e t V C u t RC s C sC R sC R U s Z s I s RC t s ( ) 1 , ( ) 1 1 1 1 ( ) ( ) ( ) − = + = + = =