
Advanced Algorithms Rounding Linear Program 尹一通Nanjing University,2022Fall
尹⼀通 Nanjing University, 2022 Fall Advanced Algorithms Rounding Linear Program

Vertex Cover
Vertex Cover
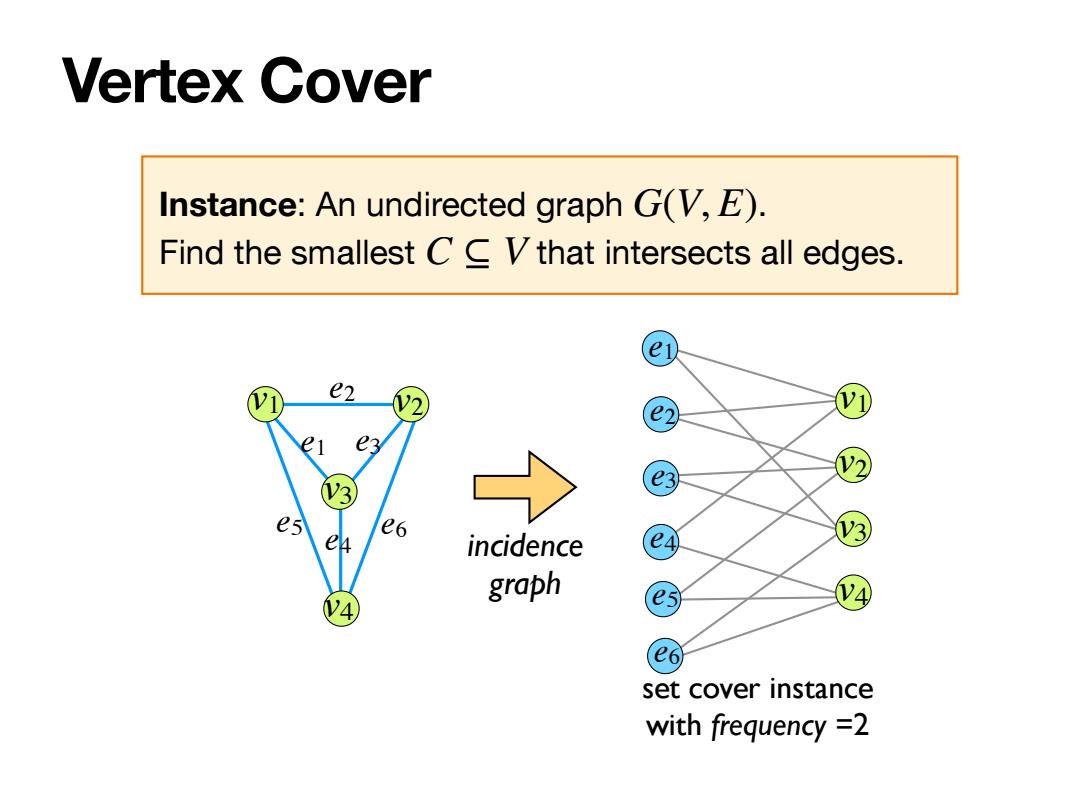
Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C V that intersects all edges. e2 e es e6 incidence graph V4 V4 set cover instance with frequency =2
Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V v1 v2 v3 v4 e1 e3 e2 e4 e1 e2 e3 e4 v1 v2 v3 e5 v4 e6 incidence graph set cover instance with frequency =2 e5 e6

Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C V that intersects all edges. ·NP-hard In(n)-approximation by greedy set cover 2-approximation algorithm: Find a maximal matching; return the matched vertices; .[Khot,Regev 2008]Assuming the unique games conjecture, there is no poly-time(2-e)-approximation algorithm
• NP-hard • -approximation by greedy set cover • 2-approximation algorithm: • [Khot, Regev 2008] Assuming the unique games conjecture, there is no poly-time -approximation algorithm. ln(n) (2 − ϵ) Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V Find a maximal matching; return the matched vertices;
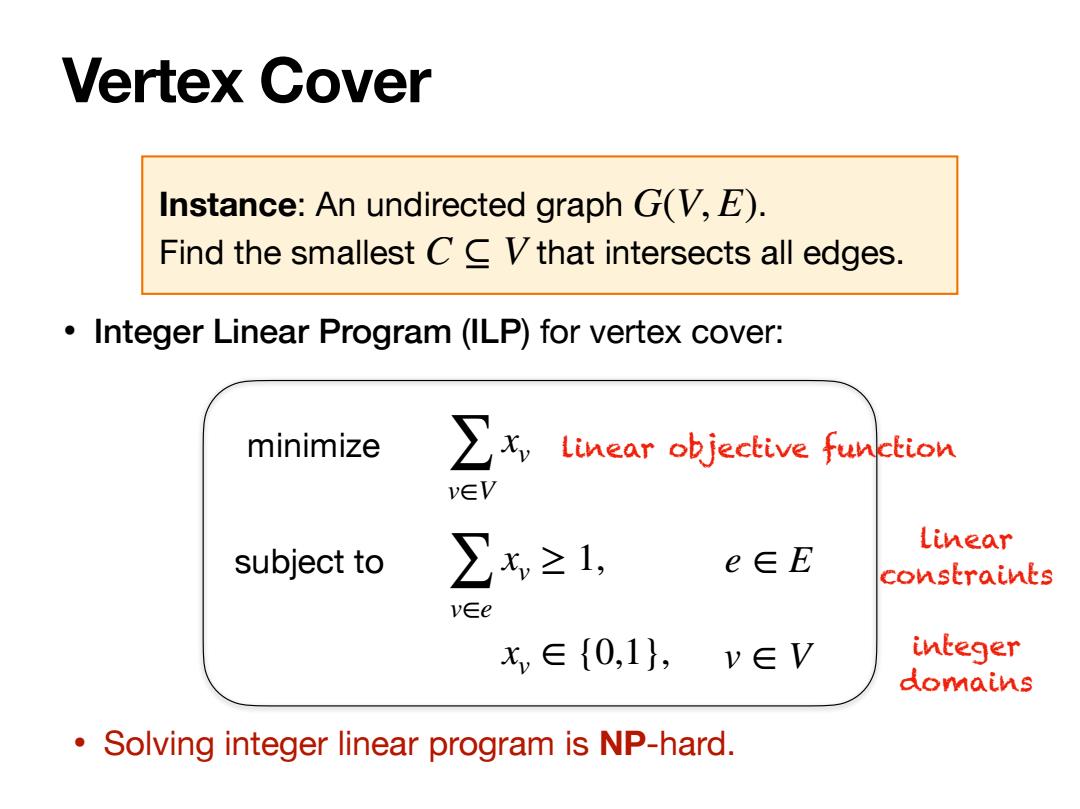
Vertex Cover Instance:An undirected graph G(V,E). Find the smallest CC Vthat intersects all edges. Integer Linear Program(ILP)for vertex cover: minimize ∑x linear objective function v∈V subject to ∑x≥1, Linear e∈E constraints v∈e x,∈{0,1},v∈V integer domains Solving integer linear program is NP-hard
• Integer Linear Program (ILP) for vertex cover: Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V linear objective function linear constraints integer domains • Solving integer linear program is NP-hard