核心重难探究 知识点 两角分别相等的两个三角形相似 【例题】如图,在口ABCD中,过点A作AE⊥BC,垂足为E,连 接DE,F为线段DE上一点,且∠AFE=∠B. B E (I)求证:△ADF~△DEC; (2)若AB=8,AD=6V3,AF=4V3,求AE的长
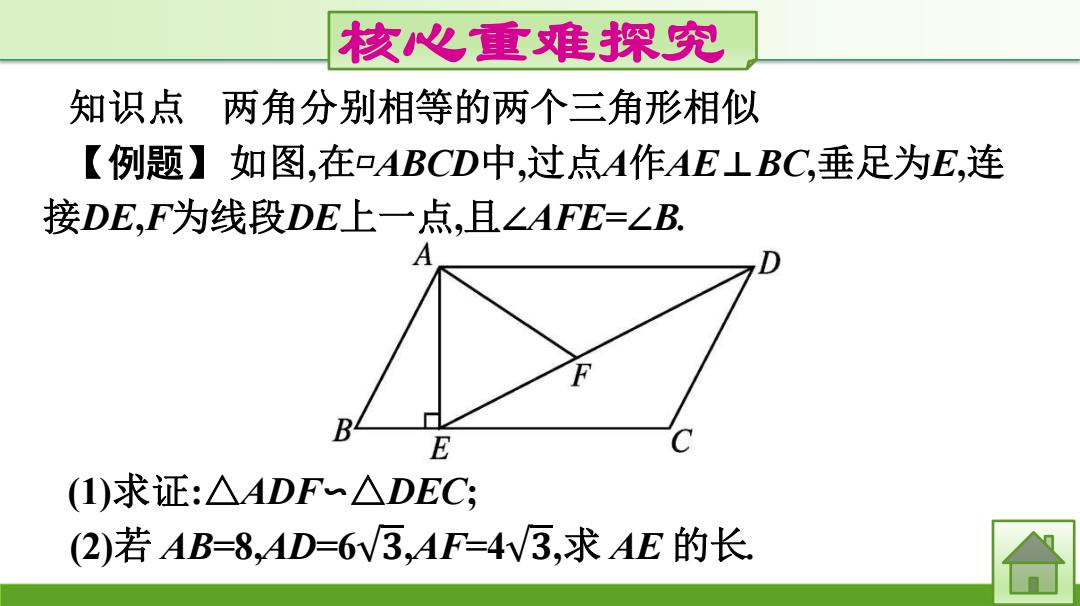
核心重难探究 知识点 两角分别相等的两个三角形相似 【例题】如图,在▱ABCD中,过点A作AE⊥BC,垂足为E,连 接DE,F为线段DE上一点,且∠AFE=∠B. (1)求证:△ADF∽△DEC; (2)若 AB=8,AD=6 𝟑,AF=4 𝟑,求 AE 的长

思路点拨:(I)已知∠AFE=∠B,你能发现∠AFE与∠AFD,∠B 与∠C有什么关系吗? (2)由已知数据与(1)中的相似三角形,如何求AD的长?进而 如何再求AE的长? 合
思路点拨:(1)已知∠AFE=∠B,你能发现∠AFE与∠AFD, ∠B 与∠C有什么关系吗? (2)由已知数据与(1)中的相似三角形,如何求AD的长?进而 如何再求AE的长?

(1)证明:.四边形ABCD是平行四边形, '.AB∥CD,AD∥BC, '.∠C+∠B=180°,∠ADF=∠DEC. .∠AFD+∠AFE=180°,∠AFE=∠B, '.∠AFD=∠C. .△ADF∽△DEC. 合
(1)证明:∵四边形ABCD是平行四边形, ∴AB∥CD,AD∥BC, ∴∠C+∠B=180° ,∠ADF=∠DEC. ∵∠AFD+∠AFE=180° ,∠AFE=∠B, ∴∠AFD=∠C. ∴△ADF∽△DEC