
第二章连续系统的时域分析 >线性连续条统的描述及其响应 >冲邀响应和阶跃响应 >卷积积分 >条统的微分算子程
¾ 线性连续系统的描述及其响应 ¾ 冲激响应和阶跃响应 ¾ 卷积积分 ¾ 系统的微分算子方程 第二章 连续系统的时域分析

2.1线性连续系统的描述及其响应 2.1.1象统的描述及微分方程的列写 描述线性时不变连续条统的数学模型是线性常系数 微分方程。 (dd dt” dt n-1 d-y0+…ay) dtn-2 06a0e0 dtm 式中an-1,..,a1,a0和bm,bm-1,.., b1,b0均为常数
2.1 线性连续系统的描述及其响应 2.1.1 系统的描述及微分方程的列写 描述线性时不变连续系统的数学模型是线性常系数 微分方程。 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 0 1 1 2 0 2 1 2 1 1 b e t dt d e t b dt d e t b a y t dt d y t a dt d y t a dt d y t m m m m m m n n n n n n n n = + + + + + − − − − − − − − − L 式中an-1,…,a1,a0和bm, bm-1,…,b1,b0均为常数

第2章连续时间系统的时域分析 ·根据实际系统的物理特性列写系统的微分方程。 对于电路系统,列写数学模型的基本依据有如下两 方面:元件特性约束和网络拓扑约束列写系统的 微分方程。 元件特性约束:表征元件特性的关条式。例如 二端元件电阻、电容、电感各自的电压与电流 的关条以及四端元件互感的初、次级电压与电 流的关系等等。 网络拓扑约束:由网络结构决定的电压电流约 束关系,KCL,KVL。 《信号与系统》
《 信号与系统》 第2章 连续时间系统的时域分析 •根据实际系统的物理特性列写系统的微分方程。 •对于电路系统,列写数学模型的基本依据有如下两 方面:元件特性约束和网络拓扑约束列写系统的 微分方程。 元件特性约束:表征元件特性的关系式。例如 二端元件电阻、电容、电感各自的电压与电流 的关系以及四端元件互感的初、次级电压与电 流的关系等等。 网络拓扑约束:由网络结构决定的电压电流约 束关系,KCL,KVL

1.元件约束VAR 在电流、电压取关联参考方向条件下: ()电阻RuR(t)=RiR(); (2)电感L, 40-9-404咖 (3)电容C,i 0=c0,u0=u+d dt (4)互感(同、异名端连接)、理想变压器等原、副边电压、 电流关系等
(2)电感L, (3)电容C, (4)互感(同、异名端连接)、理想变压器等原、副边电压、 电流关系等。 0 0 () 1 () , ( ) ( ) t L L LL L t di t ut L i it u d dt L = =+ τ τ ∫ 0 0 () 1 () , () ( ) ( ) t C C CC C t du t it C ut ut i d dt C = =+ τ τ ∫ 1. 元件约束VAR 在电流、电压取关联参考方向条件下: (1)电阻R uR(t)=R·iR(t);
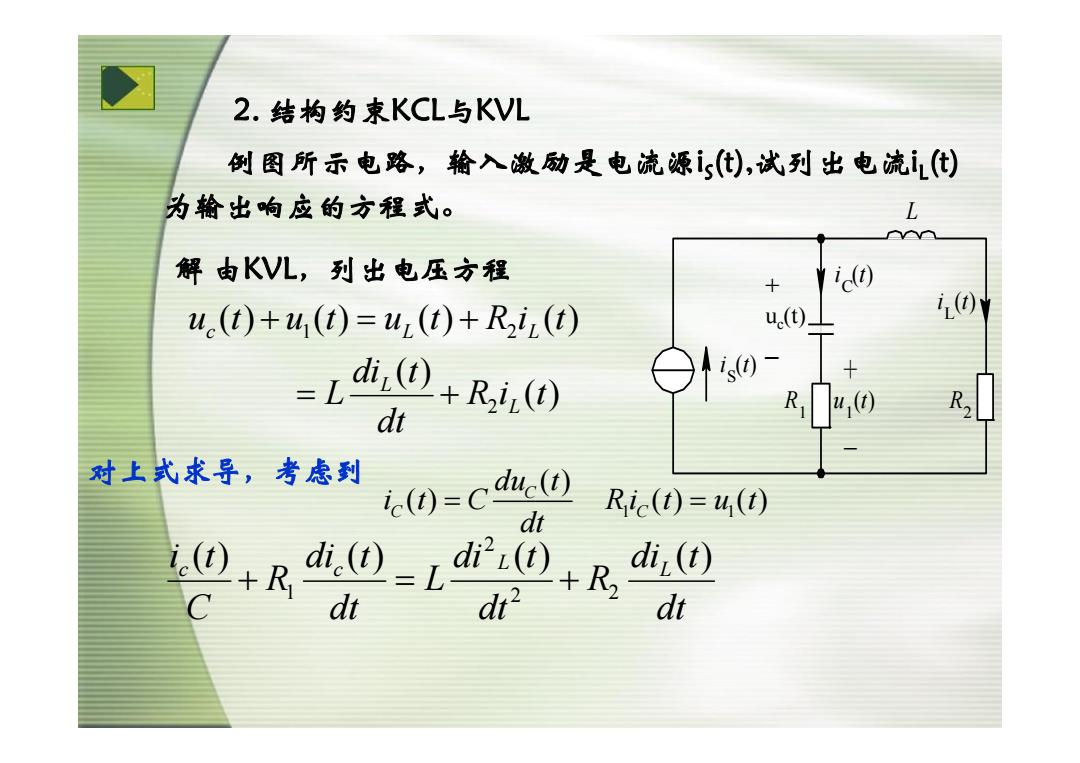
2.结构约束KCL与KVL 例图所示电路,输入激励是电流源i(),试到出电流i() 为输出响应的方程式。 L 解由KVL,列出电压方程 i) u.(t)+u,(t)=uz(t)+R2(t) u.(t)1 0州 =Ld0+R,(回 Ru ( R dt 对上式求导,考虑到 ()=c) Ric(t)=u(t)) dt di(=L i.()Rdt i()R i(t) 2 di
2. 结构约束KCL与KVL 例图所示电路,输入激励是电流源iS(t),试列出电流iL(t) 为输出响应的方程式。 iS(t) iC(t) u1(t) iL(t) R2 R1 L + - + uc(t) _ ( ) ( ) ( ) ( ) ( ) ( ) 2 1 2 R i t dt di t L u t u t u t R i t L L c L L = + + = + 解 由KVL,列出电压方程 对上式求导,考虑到 1 1 ( ) () () () C C C du t i t C Ri t u t dt = = dt di t R dt di t L dt di t R C i t L L c c ( ) ( ) ( ) ( ) 2 2 2 + 1 = +