
第8章离散时间系统的Z域分析 8.1离散信号的z变换及收敛域 8.2z逆变换 8.3z变换的基本性质 8.4利用z变换解差分方程 8.5离散系统的系统函数 8.6序列的傅里叶变换 8.7离散时间系统的频率响应特性
第8章 离散时间系统的z域分析 8.1 离散信号的 z变换及收敛域 8.2 z逆变换 8.3 z变换的基本性质 8.4 利用 z变换解差分方程 8.5 离散系统的系统函数 8.6 序列的傅里叶变换 8.7离散时间系统的频率响应特性

本章主要内容 (1)Z变换、性质及其收敛域 (2)利用z变换求解差分方程 (3)离散系统的系统函数 (4)系统稳定性及因果性
(1) Z变换、性质及其收敛域 (2) 利用z变换求解差分方程 (3) 离散系统的系统函数 (4) 系统稳定性及因果性 本章主要内容

8.1离散信号的z变换及收敛域 8.1.1z变换定义 z变换的定义可以由取样信号的拉氏变换引出, 也可以直接对离散信号给予定义。 x[n的双边z变换:X(a)=∑n” 17=-0 =+x灯-2]p2+[-12+x0]++x[2]z2+… x[刀]的单边z变换:X(a)=z(列=∑”=0]++22+… 对z变换式的理解xa)=xm2”=-2z+2 的正幂 +x0)z°+x①)z1+x2)z2+xz"+.. 1)X(z)是z1的幂级数2)级数的系数是x(n) 的负暴 3)幂-n中的n指出x(n)的位置
8.1 离散信号的z 变换及收敛域 z变换的定义可以由取样信号的拉氏变换引出, 也可以直接对离散信号给予定义。 8.1.1 z 变换定义 x[n]的双边z 变换: =L+ − + − + + + +L = − − − +∞ =−∞ ∑ 2 1 1 2 [ 2] [ 1] [0] [1] [2] ( ) [ ] x z x z x x z x z X z x n z n n x[n]的单边z 变换: ( ) 1 2 0 ( ) [ ] [ ] [0] [1] [2] n n X z xn xnz x x z x z ∞ − −− = =Z = =+ + + ∑ L ∑ ∞ =−∞ − = n n X(z) x(n)z 14 2 44444 4444443 L K 14 2 44 4 3 44 K 的负幂 的正幂 z n z x z x z x z x n z x z x z + + + + + = − + − − − − (0) (1) (2) ( ) ( 2) ( 1) 0 1 2 对 2 1 z变换式的理解 1)X (z)是 z −1的幂级数 3)幂− n中的n指出 x(n) 的位置 2)级数的系数是 x (n)
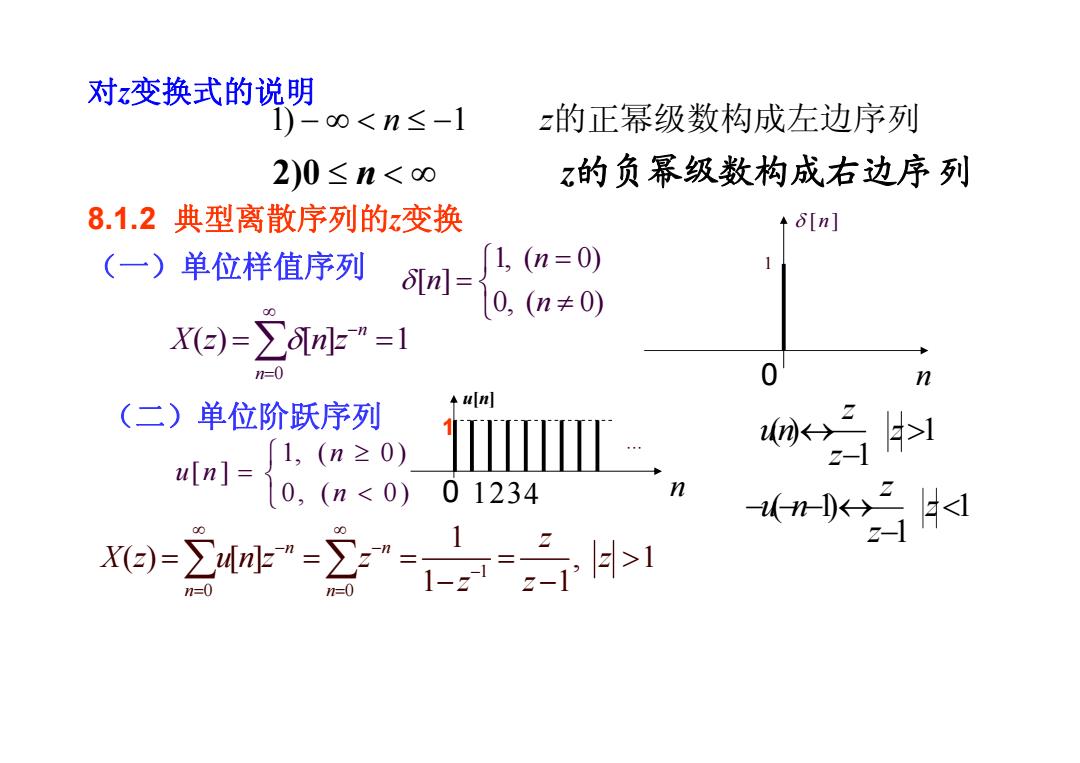
对z变换式的说明 1)-o<n≤-1 z的正幂级数构成左边序列 2)0≤n<o z的负幂级数构成右边序列 8.1.2典型离散序列的z变换 +6[n] (一)单位样值序列 6[n= 1,(n=0) 0,(n≠0) Xe)=∑n"=1 =0 0 n + (二)单位阶跃序列 l10.(123 z-1 xe-立4-2之=>l n等
对 z变换式的说明 2 ) 0 ≤ n < ∞ z的负幂级数构成右边序 列 1 ) − ∞ < n ≤ − 1 z的正幂级数构成左边序 列 8.1.2 典型离散序列的 z变换 (一)单位样值序列 1, ( 0) [ ] 0, ( 0) n n n δ ⎧ = = ⎨ ⎩ ≠ 0 n 1 δ [ ] n 0 () [] 1 n n X z nz δ ∞ − = = = ∑ (二)单位阶跃序列 1, ( 0) [ ] 0, ( 0) n u n n ⎧ ≥ = ⎨ ⎩ < u[n] 0 1 123 4 n L 1 0 0 1 () [] , 1 1 1 n n n n z X z unz z z z z ∞ ∞ − − − = = = === > − − ∑ ∑ 1 1 ( 1) < − − − − ↔ z z z u n 1 1 ( ) > − ↔ z z z u n
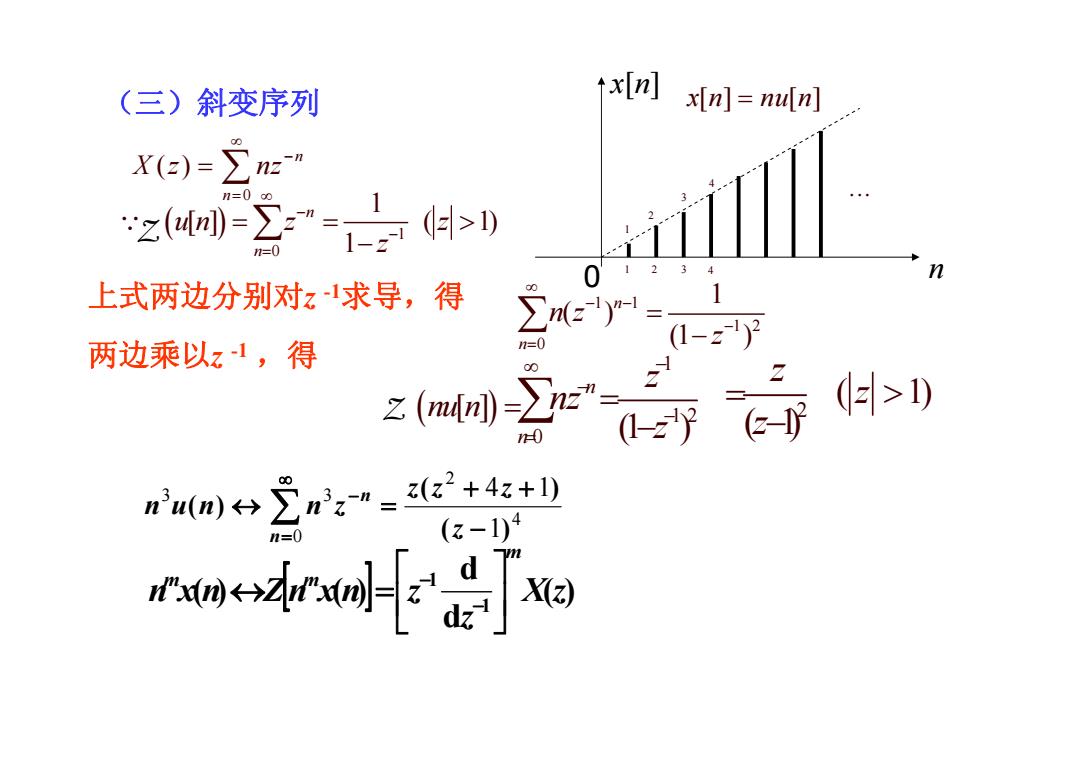
(三)斜变序列 txIn]xin]=nuln] X(e)-∑ne" z2) 7=0 1=0 0 12 n 上式两边分别对z求导,得 ∑ey=, (1-z)2 两边乘以z1,得 1=0 之(ma)∑e”- (2>1) 0 0-z 2- nu(m)9∑n2"=2(22+4z+ 0 (z-1)4 awor-x
0 ( ) n n X z nz ∞ − = = ∑ ( ) 1 0 1 [ ] ( 1) 1 n n un z z z ∞ − − = == > − QZ ∑ x [ n ] 0 n 1 1 2 2 3 3 4 4 L (三)斜变序列 x[] [] n nu n = 上式两边分别对z -1求导,得 1 1 1 2 0 1 ( ) (1 ) n n n z z ∞ − − − = = − ∑ 两边乘以z -1 ,得 1 1 2 0 (1 ) n n z nz z ∞ − − − = = − ∑ 2 ( 1) z z = − Z (nu n[ ] ) = ( 1) z > 4 2 0 3 3 1 4 1 ( ) ( ) ( ) − + + ↔ = − ∞ = ∑ z z z z n u n n z n n [ ] ( ) d d ( ) ( ) 1 1 X z z n x n Z n x n z m m m ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ↔ = − −