
共同的思路: 。 由于异方差性是相对于不同的解释变量观测值, 随机误差项具有不同的方差。那么检验异方差 性,也就是检验随机误差项的方差与解释变量 观测值之间的相关性及其相关的“形式”。 问题在于用什么来表示随机误差项的方差?一 般的处理方法:首先采用OLS估计,得到残差 估计值,用它的平方近似随机误差项的方差。 e=y,-(,)os Var(4)=E(42)≈e2
共同的思路: • 由于异方差性是相对于不同的解释变量观测值, 随机误差项具有不同的方差。那么检验异方差 性,也就是检验随机误差项的方差与解释变量 观测值之间的相关性及其相关的“形式”。 • 问题在于用什么来表示随机误差项的方差?一 般的处理方法:首先采用OLS估计,得到残差 估计值,用它的平方近似随机误差项的方差。 ~ e y ( y ) i = i − i 0ls Var E e i i i ( ) ( ) ~ = 2 2

2、图示法 (1)用X-Y的散点图进行判断 看是否存在明显的散点扩大、缩小或复杂型 趋势(即不在一个固定的带型域中)。 (2)X-e,的散点图进行判断 看是否形成一斜率为零的直线
2、图示法 (1)用X-Y的散点图进行判断 看是否存在明显的散点扩大、缩小或复杂型 趋势(即不在一个固定的带型域中)。 (2)X-~ ei 2 的散点图进行判断 看是否形成一斜率为零的直线
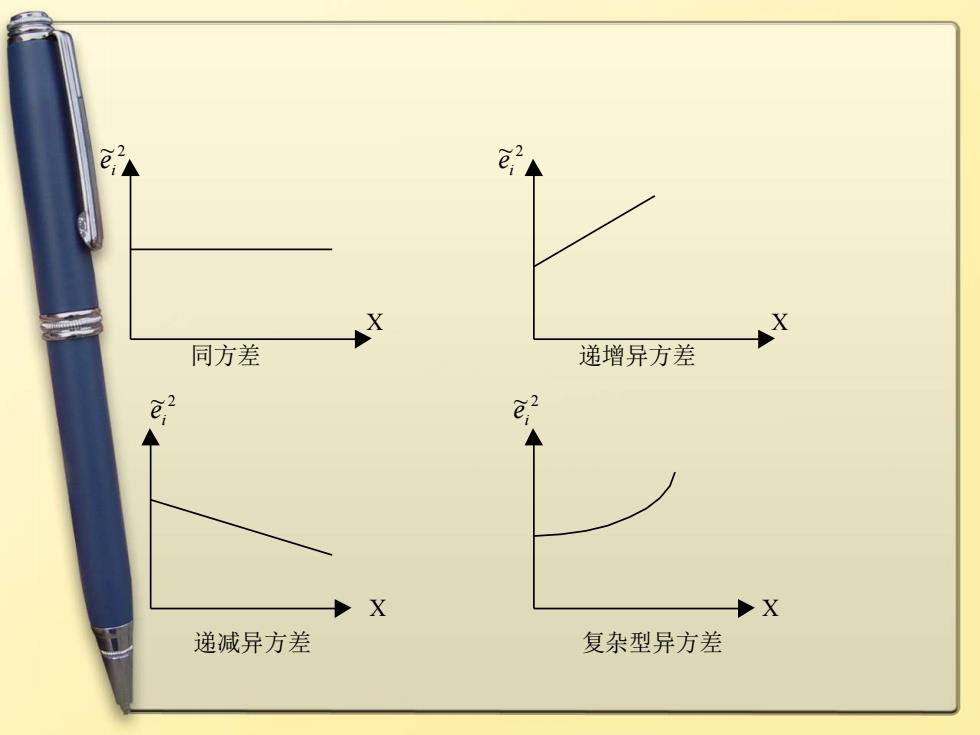
同方差 递增异方差 ®2 X 递减异方差 复杂型异方差
~ei 2 ~ei 2 X X 同方差 递增异方差 ~ei 2 ~ei 2 X X 递减异方差 复杂型异方差

3、帕克(Park)检验与戈里瑟(Gleiser)检验 基本思想:偿试建立方程: Park &=f(Xn)+8 @=f(Xj)+E Gleiser 选择关于变量X的不同的函数形式,对方程进行估计并 进行显著性检验,如果存在某一种函数形式,使得方程 显著成立,则说明原模型存在异方差性。 。 帕克检验常用的函数形式: f(Xn)=a2Xue" Ine2)=Ino2+aln+ 若o在统计上是显著的,表明存在异方差性
3、帕克(Park)检验与戈里瑟(Gleiser)检验 • 基本思想:偿试建立方程: i X ji i e = f ( ) + ~2 i X ji i e |= f ( ) + ~| 选择关于变量X的不同的函数形式,对方程进行估计并 进行显著性检验,如果存在某一种函数形式,使得方程 显著成立,则说明原模型存在异方差性。 i f X X e ji ji 2 ( ) = i X ji i e ) = ln + ln + ~ ln( 2 2 若在统计上是显著的,表明存在异方差性。 • 帕克检验常用的函数形式: Park Gleiser

4、 戈德菲尔德-匡特(Goldfeld-Quandt)检 验 G-Q检验以F检验为基础,适用于样本容量较 大、异方差递增或递减的情况。 先将样本一分为二,对子样①和子样②分别作 回归,然后利用两个子样的残差平方和之比构 造统计量进行异方差检验。 由于该统计量服从F分布,因此假如存在递增 的异方差,则F远大于1;反之就会等于1(同 方差)或小于1(递减方差)
4、戈德菲尔德-匡特(Goldfeld-Quandt)检 验 • G-Q检验以F检验为基础,适用于样本容量较 大、异方差递增或递减的情况。 • 先将样本一分为二,对子样①和子样②分别作 回归,然后利用两个子样的残差平方和之比构 造统计量进行异方差检验。 • 由于该统计量服从F分布,因此假如存在递增 的异方差,则F远大于1;反之就会等于1(同 方差)或小于1(递减方差)