
第三节 流体动力学方程——流体在管内流动的基本方程 一、几个概念: 体积流量 ( ) v q ——单位时间流过导管任一截面的流体体积, 3 1 m s − ; 质量流量 ( ) m q ——单位时间流过导管任一截面的流体质量, 1 kg s − ; 质量流量( ) m q 1 kg s − =体积流量 3 1 m s − 流体密度= 3 1 3 m s kg m − − v q 流速 (u) ——流体质点于单位时间内在导管中流过的距离, 1 m s − 流速 ( ) ( ) (A) q u v 导管截面积 体积流量 = 稳定流动与不稳定流动:流体在管内流动时,在任一点上,它的流速、 压力等有关物理参数不随时间变化,称稳定流动。 本课程研究稳定流动
第三节 流体动力学方程——流体在管内流动的基本方程 一、几个概念: 体积流量 ( ) v q ——单位时间流过导管任一截面的流体体积, 3 1 m s − ; 质量流量 ( ) m q ——单位时间流过导管任一截面的流体质量, 1 kg s − ; 质量流量( ) m q 1 kg s − =体积流量 3 1 m s − 流体密度= 3 1 3 m s kg m − − v q 流速 (u) ——流体质点于单位时间内在导管中流过的距离, 1 m s − 流速 ( ) ( ) (A) q u v 导管截面积 体积流量 = 稳定流动与不稳定流动:流体在管内流动时,在任一点上,它的流速、 压力等有关物理参数不随时间变化,称稳定流动。 本课程研究稳定流动

二、管内流体的质量衡算——连续性方程 1 1 2 2 有: 1 1 1 2 2 2 1 1 2 2 1 1 1 2 2 2 1 2 u A u A A u A u u A u A q m q m = = = = 气体: 液体:
二、管内流体的质量衡算——连续性方程 1 1 2 2 有: 1 1 1 2 2 2 1 1 2 2 1 1 1 2 2 2 1 2 u A u A A u A u u A u A q m q m = = = = 气体: 液体:

三、管内流体的机械能衡算 1、理想流体的机械能衡算——柏努利方程 理想流体: 常数 常数 常数 + + = + + = + + = + + = −−−− = + + = + + = g P g u Z g P g u Z m P V g Z u P g Z u mgZ m u PV mgZ m u P V 2 2 2 2 2 1 2 2 1 1 2 2 1 2 2 1 2 2 1 1 2 1 1 2 2 2 2 1 1 2 2 1 2 1 1
三、管内流体的机械能衡算 1、理想流体的机械能衡算——柏努利方程 理想流体: 常数 常数 常数 + + = + + = + + = + + = −−−− = + + = + + = g P g u Z g P g u Z m P V g Z u P g Z u mgZ m u PV mgZ m u P V 2 2 2 2 2 1 2 2 1 1 2 2 1 2 2 1 2 2 1 1 2 1 1 2 2 2 2 1 1 2 2 1 2 1 1
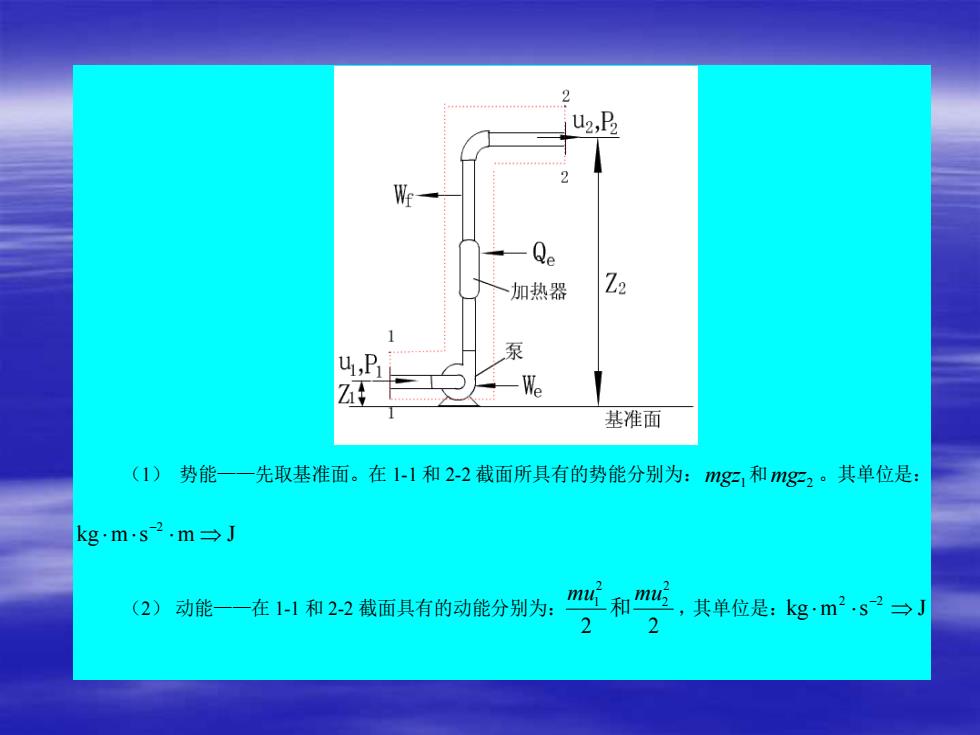
(1) 势能——先取基准面。在 1-1 和 2-2 截面所具有的势能分别为:mgz1和mgz2 。其单位是: kg m s m J −2 (2) 动能——在 1-1 和 2-2 截面具有的动能分别为: 2 2 2 2 2 mu1 mu 和 ,其单位是:kg m s J 2 −2
(1) 势能——先取基准面。在 1-1 和 2-2 截面所具有的势能分别为:mgz1和mgz2 。其单位是: kg m s m J −2 (2) 动能——在 1-1 和 2-2 截面具有的动能分别为: 2 2 2 2 2 mu1 mu 和 ,其单位是:kg m s J 2 −2
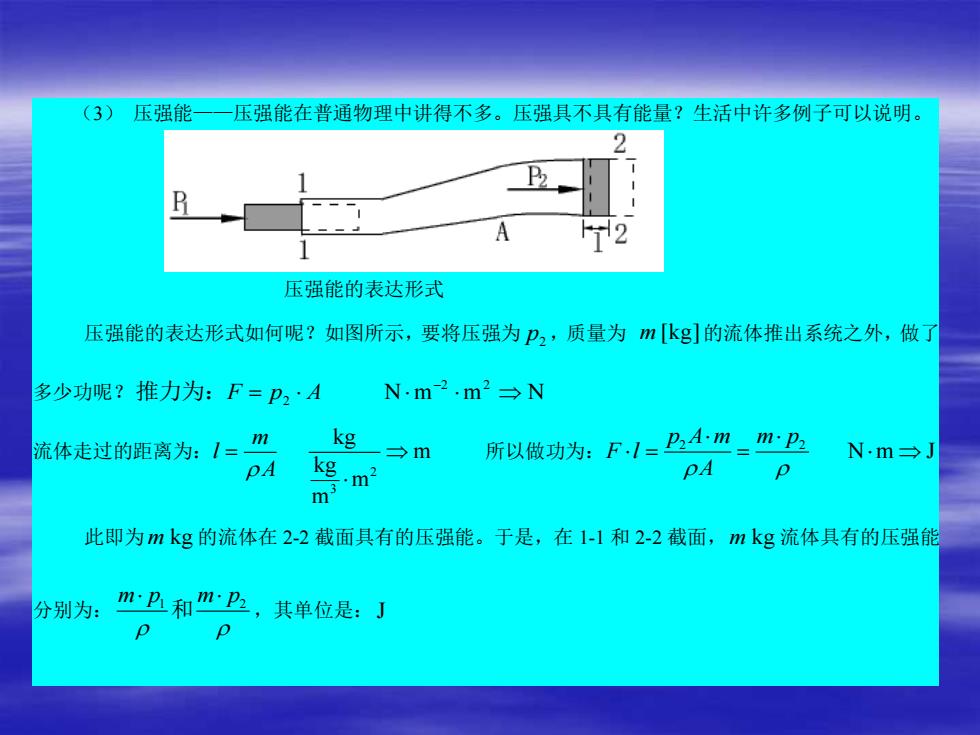
(3) 压强能——压强能在普通物理中讲得不多。压强具不具有能量?生活中许多例子可以说明。 压强能的表达形式 压强能的表达形式如何呢?如图所示,要将压强为 p2,质量为 m [kg]的流体推出系统之外,做了 多少功呢? N m m N 2 2 推力为:F = p2 A − 流体走过的距离为: 2 3 kg m kg m m m l A = 所以做功为: 2 2 N m J p A m m p F l A = = 此即为m kg 的流体在 2-2 截面具有的压强能。于是,在 1-1 和 2-2 截面,m kg 流体具有的压强能 分别为: m p m p 1 2 和 ,其单位是:J
(3) 压强能——压强能在普通物理中讲得不多。压强具不具有能量?生活中许多例子可以说明。 压强能的表达形式 压强能的表达形式如何呢?如图所示,要将压强为 p2,质量为 m [kg]的流体推出系统之外,做了 多少功呢? N m m N 2 2 推力为:F = p2 A − 流体走过的距离为: 2 3 kg m kg m m m l A = 所以做功为: 2 2 N m J p A m m p F l A = = 此即为m kg 的流体在 2-2 截面具有的压强能。于是,在 1-1 和 2-2 截面,m kg 流体具有的压强能 分别为: m p m p 1 2 和 ,其单位是:J