
真空度=当地大气压-系统绝压 =-(系统绝压-当地大气压) =-表压 例如某系统真空度为 200mmHg,当地大气压为 101.3kPa, 则:表压=-真空度=-200/760*101.3=-26.7kPa 系统绝压=表压+当地大气压 表压等于系统绝压减去当地大气压,而真空度是当地大气压减 去系统绝压。真空度正好是负的表压。比如某系统的真空度为 200mmHg,则系统的表压为-200mmHg。如果当地大气压等于 760mmHg,该系统的绝压为,表压加上当地大气压,等于 560mmHg
真空度=当地大气压-系统绝压 =-(系统绝压-当地大气压) =-表压 例如某系统真空度为 200mmHg,当地大气压为 101.3kPa, 则:表压=-真空度=-200/760*101.3=-26.7kPa 系统绝压=表压+当地大气压 表压等于系统绝压减去当地大气压,而真空度是当地大气压减 去系统绝压。真空度正好是负的表压。比如某系统的真空度为 200mmHg,则系统的表压为-200mmHg。如果当地大气压等于 760mmHg,该系统的绝压为,表压加上当地大气压,等于 560mmHg

1[atm] = 101330 Pa = 10.34米水柱=1.033工程大气压= 760 mmHg 空气 1.293 kg m 0.0173cp 3 = = − , 3 0.0173 10− = SI 单位, 1 1 1.01 kJ kg K − − = Cp ,管内流速取 1 8 ~ 15 m s − 水 1000 kg m 1cp 3 = = − , 3 1 10− = SI 单位, 1 1 4.187 kJ kg K − − = Cp , 管内流速取 1 1 ~ 3 m s − 常用数据和单位
1[atm] = 101330 Pa = 10.34米水柱=1.033工程大气压= 760 mmHg 空气 1.293 kg m 0.0173cp 3 = = − , 3 0.0173 10− = SI 单位, 1 1 1.01 kJ kg K − − = Cp ,管内流速取 1 8 ~ 15 m s − 水 1000 kg m 1cp 3 = = − , 3 1 10− = SI 单位, 1 1 4.187 kJ kg K − − = Cp , 管内流速取 1 1 ~ 3 m s − 常用数据和单位
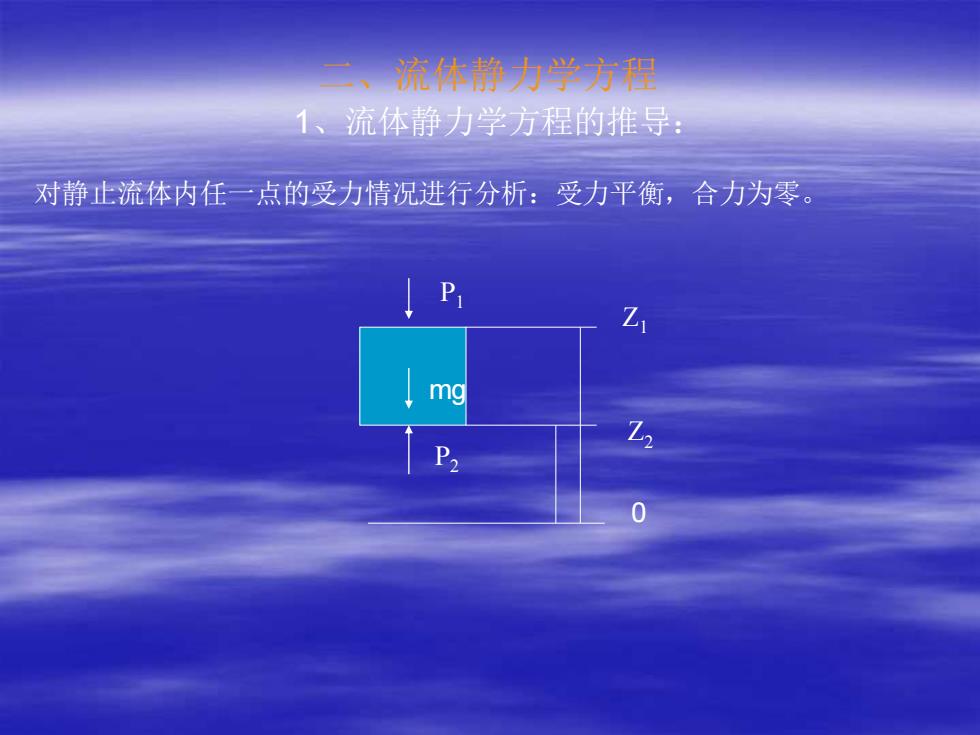
二、流体静力学方程 1、流体静力学方程的推导: 对静止流体内任一点的受力情况进行分析:受力平衡,合力为零。 P1 mg P2 0 Z2 Z1
二、流体静力学方程 1、流体静力学方程的推导: 对静止流体内任一点的受力情况进行分析:受力平衡,合力为零。 P1 mg P2 0 Z2 Z1

设受力向上为正:有 P1 =p1A P2 =p2 A mg=ρVg=ρA(Z1-Z2)g 可得: P2 =P1+ρ(Z1-Z2)g 或 Z1-Z2=(P2-P1)/ρg P1 /ρg+Z1 =P2 /ρg+Z2=常数 讨论: ①流体内任一点压力大小与相邻点压力及流体密度、该点位置有关; ②压力或压差的大小可以用液体的液柱高低表示; ③流体内任一点机械能守恒,P/ρg ——静压头, Z——位压头
设受力向上为正:有 P1 =p1A P2 =p2 A mg=ρVg=ρA(Z1-Z2)g 可得: P2 =P1+ρ(Z1-Z2)g 或 Z1-Z2=(P2-P1)/ρg P1 /ρg+Z1 =P2 /ρg+Z2=常数 讨论: ①流体内任一点压力大小与相邻点压力及流体密度、该点位置有关; ②压力或压差的大小可以用液体的液柱高低表示; ③流体内任一点机械能守恒,P/ρg ——静压头, Z——位压头

2、流体静力学方程的应用: 压力测定 液位高度测定 液封高度测定 仪器——U型管压差计
2、流体静力学方程的应用: 压力测定 液位高度测定 液封高度测定 仪器——U型管压差计