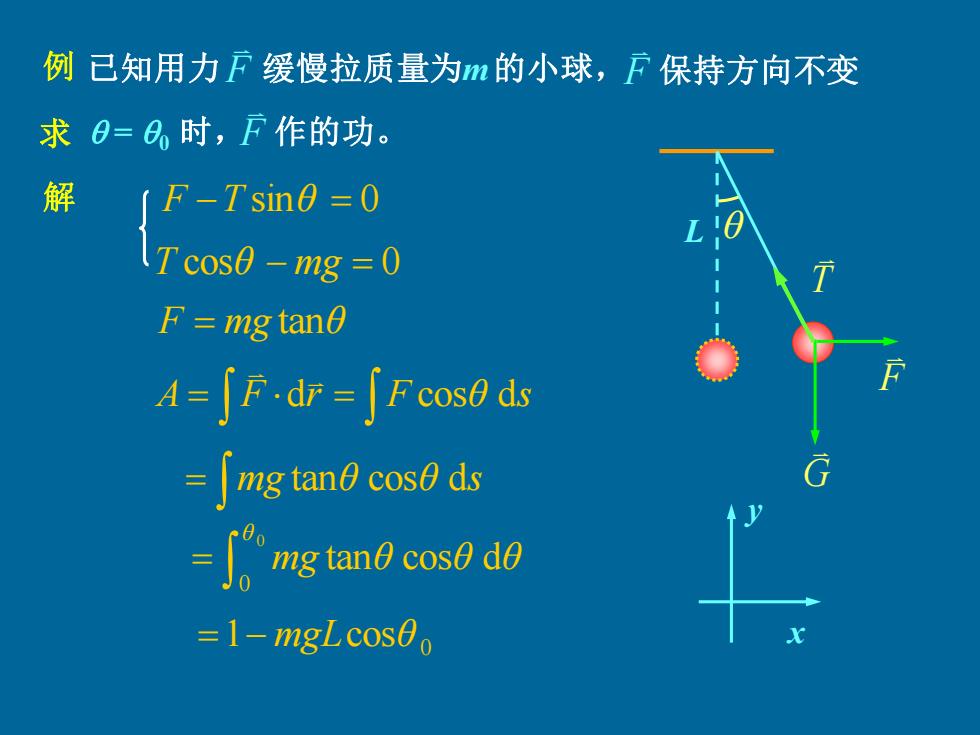
例已知用力F缓慢拉质量为m的小球,F保持方向不变 求0=0时,F作的功。 解 (F-Tsin0 =0 Tcos0 -mg =0 F=mg tan0 A=JF.d=∫Fcos0ds [mg tan0 cos0 ds mg tano cos0 do =1-mgLcos0
F L 缓慢拉质量为m 的小球, 解 F −T sinθ = 0 T cosθ − mg = 0 F = mg tanθ = mg tanθ cosθ ds x y A = F dr = F cosθ ds θ G T 0 =1− mgLcosθ 例 求 = 0 时, 已知用力 F F 保持方向不变 F 作的功。 = 0 0 tan cos d θ mg θ θ θ

例已知m=2kg,在F=12t作用下由静止做直线运动 求t=0→2s内F作的功及t=2s时的功率。 dv 解 兰=6t三 v=312=dx →dx=3rdi 4-d=3rdr=36r'd1=144J P=F,D=121:3t2=288W
已知 m = 2kg , 在 F = 12t 作用下由静止做直线运动 解 t t m F d d 6 v = = t x t d d 3 2 v = = dx 3t dt 2 = 36 d 144J 2 0 3 = = t t =12t 3t 2 = 288W = x A F x 0 d = t F t t 0 2 3 d v P = F 例 求 t = 0→2s内F 作的功及t = 2s 时的功率
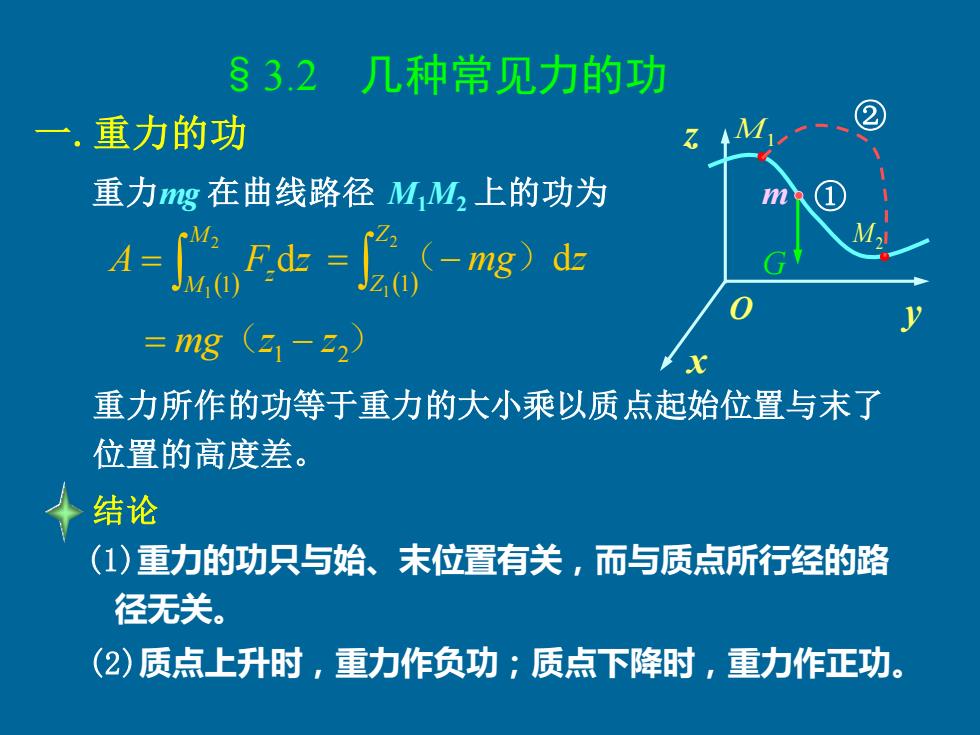
S32 几种常见力的功 一,重力的功 重力g在曲线路径M,M,上的功为 A=必t=w-g)d正 =mg(21-22 重力所作的功等于重力的大小乘以质点起始位置与末了 位置的高度差。 ◆结论 (1)重力的功只与始、未位置有关,而与质点所行经的路 径无关。 (2)质点上升时,重力作负功;质点下降时,重力作正功:
x y z O §3.2 几种常见力的功 一.重力的功 重力mg 在曲线路径 M1M2 上的功为 ( ) = 2 1 1 d M M z A F z ( ) = − 2 1 1 d Z Z ( mg) z = mg(z1 − z2) 重力所作的功等于重力的大小乘以质点起始位置与末了 位置的高度差。 (1)重力的功只与始、末位置有关,而与质点所行经的路 径无关。 (2)质点上升时,重力作负功;质点下降时,重力作正功。 M1 M2 m G 结论 ② ①
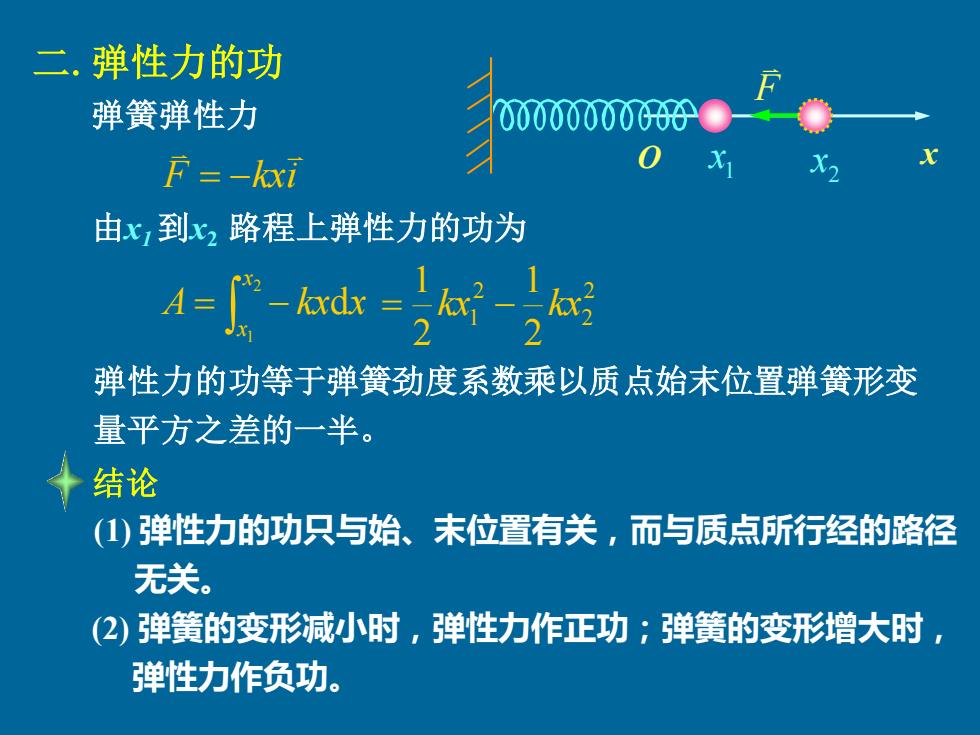
二.弹性力的功 弹簧弹性力 000000000094 F=-kxi 由x,到x2路程上弹性力的功为 A=-kd=-树 弹性力的功等于弹簧劲度系数乘以质点始末位置弹簧形变 量平方之差的一半。 结论 (1)弹性力的功只与始、末位置有关,而与质点所行经的路径 无关。 (2)弹簧的变形减小时,弹性力作正功;弹簧的变形增大时, 弹性力作负功
二.弹性力的功 = − 2 1 d x x A kx x (1) 弹性力的功只与始、末位置有关,而与质点所行经的路径 无关。 (2) 弹簧的变形减小时,弹性力作正功;弹簧的变形增大时, 弹性力作负功。 2 2 2 1 2 1 2 1 = kx − kx 1 x 2 x F F kxi = − 弹簧弹性力 由x1 到x2 路程上弹性力的功为 弹性力的功等于弹簧劲度系数乘以质点始末位置弹簧形变 量平方之差的一半。 结论 O x
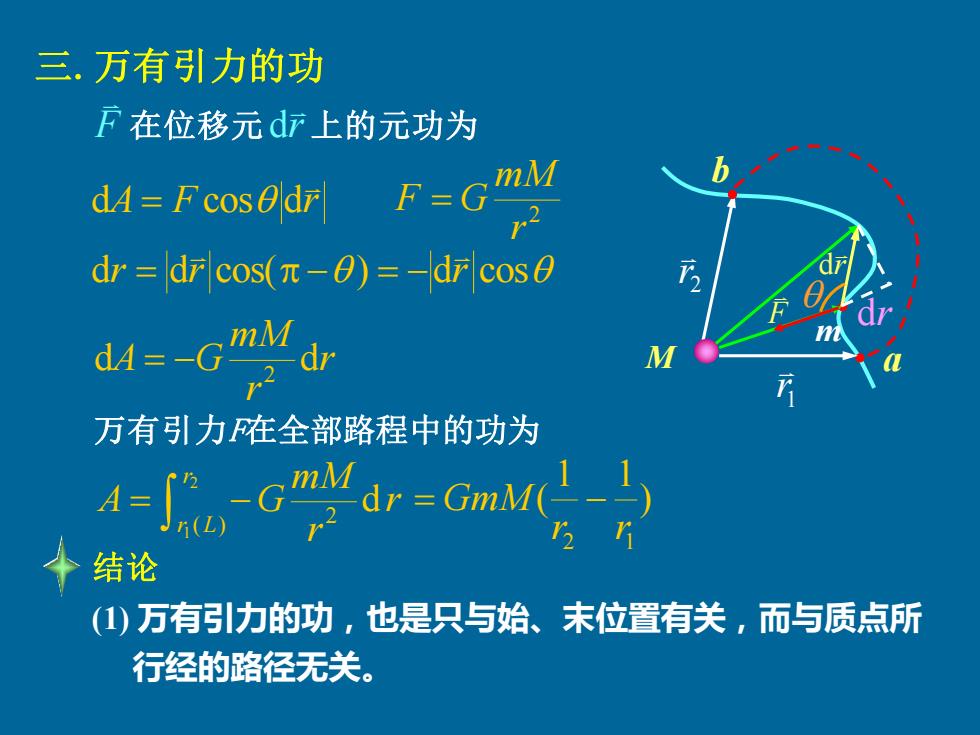
三.万有引力的功 F在位移元d析上的元功为 F=G r2 dr dr cos(n-0)=-dcose A-G 万有引力在全部路程中的功为 dr-GmMn 十结论 (1)万有引力的功,也是只与始、未位置有关,而与质点所 行经的路径无关
三.万有引力的功 上的元功为 A F r d = cos d dr dr cos( ) dr cos = − = − r r mM dA G d 2 = − 万有引力F在全部路程中的功为 = − 2 1 ( ) 2 d r r L r r mM A G ) 1 1 ( 2 1 r r = GmM − (1) 万有引力的功,也是只与始、末位置有关,而与质点所 行经的路径无关。 M a b 1 r 2 r m F r d 结论 F 在位移元 r d 2 r mM F = G dr