
1624/12/23 【例1】己知g、1、E1、求转角方程和挠度方程、并 确定最大转角和最大挠度。 1.求支座反力 ql F=Fg= 2 2.列弯矩方程 M(x)-4x-4x (0≤x≤) 2 2 3.列微分方程 Elo”= 2 2
2024/12/23 16 【例1】已知q、l、EI、求转角方程和挠度方程、并 确定最大转角和最大挠度。 1.求支座反力 2 A B ql F F = = A q B C F l A FB 2.列弯矩方程 x 2 ( ) (0 ) 2 2 ql q M x x x x l = − 3.列微分方程 2 2 2 ql q EI x x = −

2024/12/23 3.列微分方程 Elo"= -x 22 积分得 Elo'= x2-9x+C 4 6 EI@= +Cx+D 12 24 D=0,C=- 24 4、确定积分常数 x=0,0A=0x=1,0B=0
2024/12/23 17 3.列微分方程 2 2 2 ql q EI x x = − ' 2 3 4 6 ql q EI x x C = − + 积分得 4、确定积分常数 0, 0; , 0. A B x x l = = = = 3 0, . 24 q D C l = = − 3 4 12 24 ql q EI x x Cx D = − + + A q B C F l A FB x
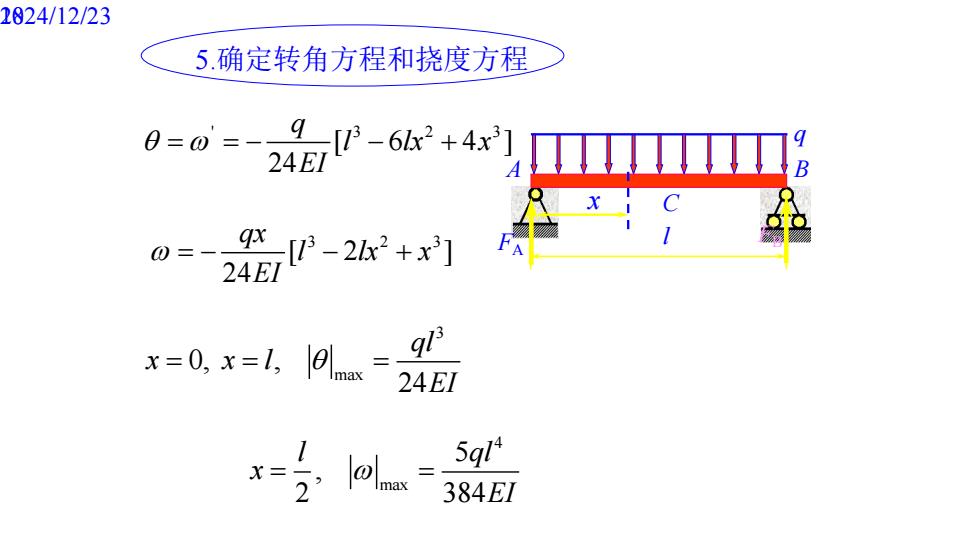
1824/12/23 5.确定转角方程和挠度方程 8=0三- 9[-6x2+4x2] 24EI 0=27P-2k2+x] 24EI x=0,x=41o=g0 24E1 x=2 5gl 384E1
2024/12/23 18 ' 3 2 3 [ 6 4 ] 24 q l lx x EI = = − − + 4 max 5 , 2 384 l ql x EI = = 3 max 0, , 24 ql x x l EI = = = 5.确定转角方程和挠度方程 3 2 3 [ 2 ] 24 qx l lx x EI = − − + A q B C F l A FB x
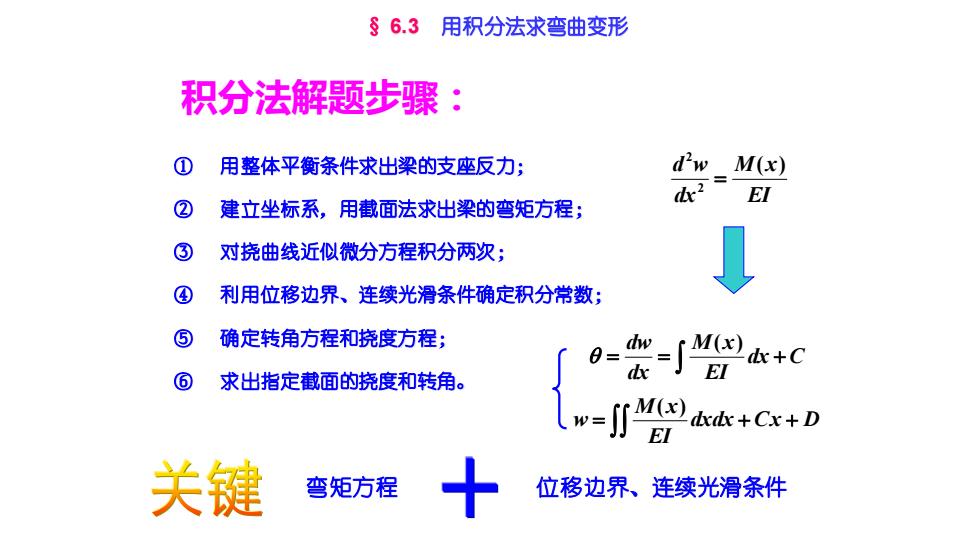
§6.3用积分法求弯曲变形 积分法解题步骤: ① 用整体平衡条件求出梁的支座反力; dw M(x) d2= EI 建立坐标系,用截面法求出梁的弯矩方程; ③ 对挠曲线近似微分方程积分两次; ④ 利用位移边界、连续光滑条件确定积分常数; ⑤ 确定转角方程和挠度方程; 0= ⑥ 求出指定截面的挠度和转角。 +D 关键 弯矩方程 位移边界、连续光滑条件
① 用整体平衡条件求出梁的支座反力; ② 建立坐标系,用截面法求出梁的弯矩方程; ③ 对挠曲线近似微分方程积分两次; ④ 利用位移边界、连续光滑条件确定积分常数; ⑤ 确定转角方程和挠度方程; ⑥ 求出指定截面的挠度和转角。 积分法解题步骤: 弯矩方程 位移边界、连续光滑条件 EI M x dx d w ( ) 2 2 = = = dx + C EI M x dx dw ( ) dxdx Cx D EI M x w = + + ( ) § 6.3 用积分法求弯曲变形

用积分法求弯曲变形 例1求梁的转角方程和挠度方程,并求最大转角和最大 挠度,梁的EI已知。 解:1)建立坐标如图,写弯矩方程 M(x)=-F(1-x) 2)列挠曲线近似微分方程 4)由位移边界条件确定积分常数 当x=0,04=04=0,04=0 43 =M(x)=-Fl+Fx C=0,D=0 3)积分求转角、挠度方程 5)转角方程和挠度方程 积分一次: E14o=EI0=-Pk+2F㎡+C E10=-Fx+Fx EIW=-Fx+Fx dr 6) 再积分一次: 确定最大转角和最大挠度 Elw=-Flx2+Fx+Cx+D F 2 6
例1 求梁的转角方程和挠度方程,并求最大转角和最大 挠度,梁的EI已知。 解:1)建立坐标如图,写弯矩方程 M x F l x ( ) ( ) = − − 2)列挠曲线近似微分方程 2 2 ( ) d EI M x dx = w d EI EI dx = w 1 1 2 3 2 6 EI Flx Fx Cx D w = − + + + 积分一次: 再积分一次: B A B l F wB = − + Fl Fx 1 2 2 = − + + Flx Fx C x 用积分法求弯曲变形 4)由位移边界条件确定积分常数 C D = = 0 0 , 3)积分求转角、挠度方程 5)转角方程和挠度方程 当x=0, ' 0 , 0 A A A = = = w w 1 2 2 EI Flx Fx = − + 1 1 2 3 2 6 EI Flx Fx w = − + 6)确定最大转角和最大挠度 2 3 max max , 2 3 B B Fl Fl x l EI EI = = = = = , w w x y