
2.可去间断点 如果f(x)在点x。的极限存在,但 limf(x)=A≠f(xo), x->xo 或f(x)在x处无定义,则称点 x为函数f(x)的可去间断点 例5讨论函数 y=1+x [2Wx, 0≤x<1, 0=1, x=1 y=2Vx 1+x, x>1, x=1处的连续性
2.可去间断点 例5 1 . 1 , 1, 1 0 1, 1, 2 , ( ) 在 处的连续性 讨论函数 = + = = x x x x x x f x o x y 1 1 2 y = 1+ x y = 2 x 为函数 的可去间断点 或 在 处无定义,则称点 如果 在点 的极限存在,但 ( ) ( ) lim ( ) ( ), ( ) 0 0 0 0 0 x f x f x x f x A f x f x x x x = →

解f(1)=1, f1-0)=2,f(1+0)=2, .imf(x)=2≠f(I), .x=0为函数的可去间断点. 可去间断点只要改变或者补充间断点处 函数的定义,则可使其变为连续点
解 f (1) = 1, f (1 − 0) = 2, f (1 + 0) = 2, lim ( ) 2 1 = → f x x f (1), x = 0为函数的可去间断点. 注意 可去间断点只要改变或者补充间断点处 函数的定义, 则可使其变为连续点
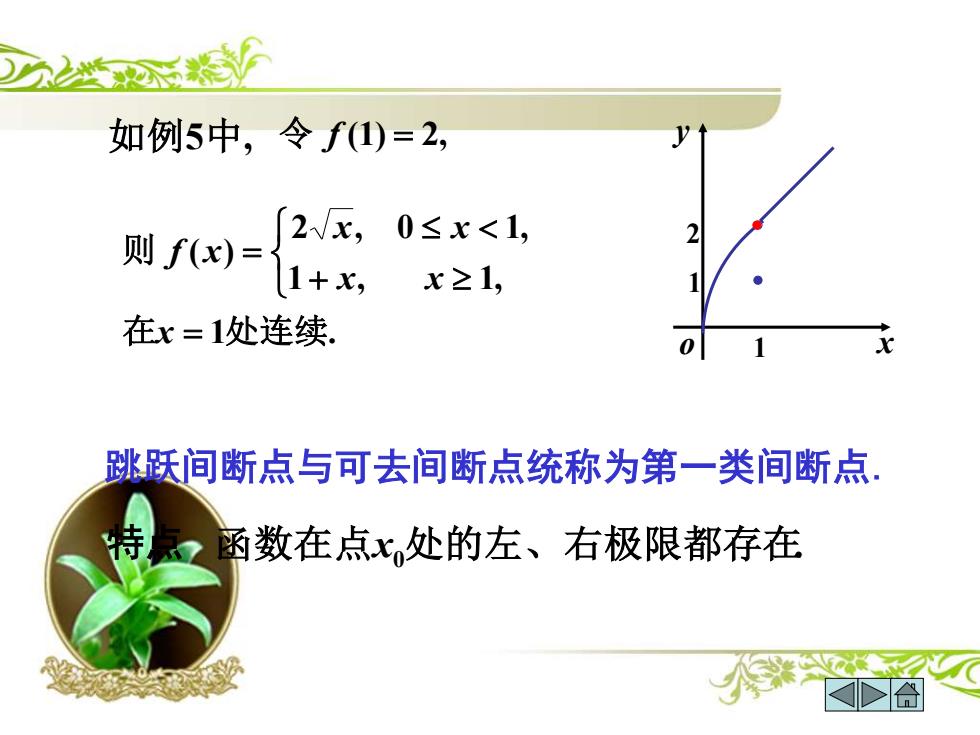
如例5中,令f)=2, 2√x, 则f()=1+x, 0≤x<1, x≥1, 在x=1处连续 跳跃间断点与可去间断点统称为第一类间断点 特 点函数在点x处的左、右极限都存在
如例5中, 令 f (1) = 2, 1 . 1 , 1, 2 , 0 1, ( ) 在 处连续 则 = + = x x x x x f x 跳跃间断点与可去间断点统称为第一类间断点. 特点 . 函数在点x0处的左、右极限都存在 o x y 1 1 2

3.第二类间断点如果f(x)在点x,处的左、 右极限至少有一个不存在,则称点x为函数 f(x)的第二类间断点. 1 例6讨论函数f(x)=了 x>0,在x=0处的连续性. x,x≤0, 解f(0-0)=0,f0+0)=+0, 为函数的第二类间断点 这种情况称为无穷间断点
3.第二类间断点 ( ) . , ( ) 0 0 的第二类间断点 右极限至少有一个不存在 则称点 为函数 如果 在点 处的左、 f x x f x x 例6 0 . , 0, , 0, 1 讨论函数 ( ) 在 = 处的连续性 = x x x x f x x 解 o x y f (0 − 0) = 0, f (0 + 0) = +, x = 1为函数的第二类间断点. 这种情况称为无穷间断点