
4.连续函数与连续区间 在区间上每一点都连续的函数,叫做在该区间上 的连续函数,或者说函数在该区间上连续, 如果函数在开区间(,b)内连续,并且在左端点 x=a处右连续,在右端点x=b处左连续,则称 函数f(x)在闭区间4,b上连续 鱼续函数的图形是一条连续而不间断的曲线
4.连续函数与连续区间 在区间上每一点都连续的函数,叫做在该区间上 的连续函数,或者说函数在该区间上连续. ( ) [ , ] . , , ( , ) , 函数 在闭区间 上连续 处右连续 在右端点 处左连续 则称 如果函数在开区间 内连续 并且在左端点 f x a b x a x b a b = = 连续函数的图形是一条连续而不间断的曲线

二、函数的间断点 函数f(x)在点x处连续必须满足的三个条件: (1)f(x)在点x处有定义; (2)limf(x)存在; x0 (3)lim f(x)=f(xo) x-→x0 果上述三个条件中要有一个不满足则称 函数(x)在点x处不连续(或间断),并称点x,为 的不连续点或间断点
二、函数的间断点 ( ) : 函 数 f x 在 点 x0处连续必须满足的三个条 件 (1) ( ) ; f x 在点x0处有定义 (2) lim ( ) ; 0 f x 存在 x→x (3) lim ( ) ( ). 0 0 f x f x x x = → ( ) ( ). ( ) ( ), , 0 0 的不连续点 或间断点 函 数 在 点 处不连续 或间断 并称点 为 如果上述三个条件中只要有一个不满足 则 称 f x f x x x

第一类间断点:可去型,跳跃型. 间断点 第二类间断点:无穷型,振荡型 (见下图)
第一类间断点:可去型,跳跃型. 第二类间断点:无穷型,振荡型. 间断点 (见下图)
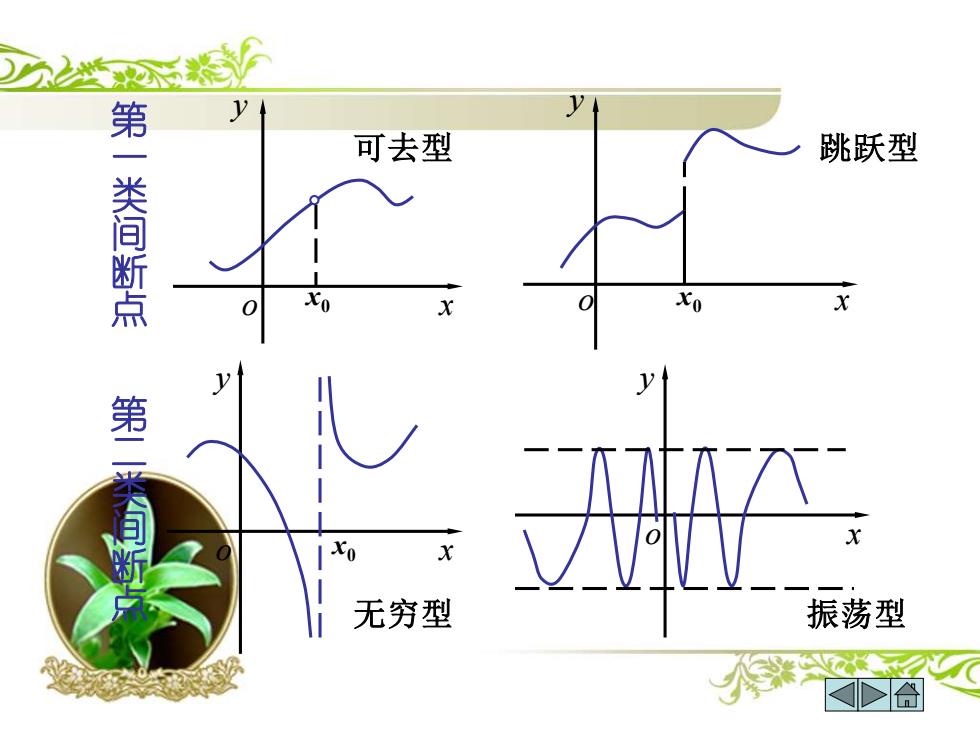
可去型 跳跃型 一类间断点 0 第 自断户 无穷型 振荡型
可去型 第一类间断点 oy x 跳跃型 无穷型 振荡型 第二类间断点 oy x 0 x oy x 0 x oy 0 x x
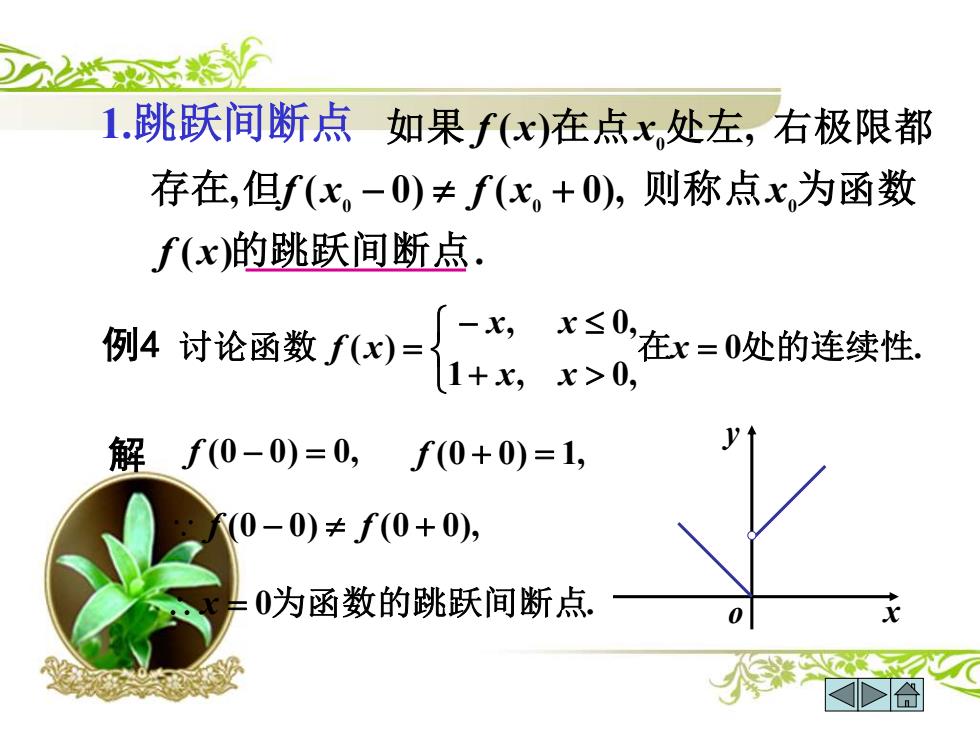
1.跳跃间断点 如果f(x)在点x处左,右极限都 存在,但f(x。-0)≠f(x。+0),则称点x,为函数 f(x)的跳跃间断点. 解时论区必-=5红=的连续性 解f(0-0)=0,f(0+0)=1, (0-0)≠f(0+0), 0为函数的跳跃间断点
1.跳跃间断点 ( ) . , ( 0) ( 0), ( ) , 0 0 0 0 的跳跃间断点 存 在 但 则称点 为函数 如 果 在 点 处 左 右极限都 f x f x f x x f x x − + 例4 0 . 1 , 0, , 0, 讨论函数 ( ) 在 = 处的连续性 + − = x x x x x f x 解 f (0 − 0) = 0, f (0 + 0) = 1, f (0 − 0) f (0 + 0), x = 0为函数的跳跃间断点. o x y