
第三节函数的极限 一、x→oo时,函数f(x)的极限 二、x→+o时,函数f(x)的极限 三、x→-o∞时,函数f(x)的极限 四、x→x时,函数f(x)的极限 x→x+0(x→x)时,函数f(x)的极限 x→x-0(x→x)时,函数f(x)的极限 小结与思考
第三节 函数的极限 一、x →时,函数 f (x)的极限 二、x →+时,函数 f (x)的极限 五、x → x + 0 (x → x0 + )时,函数 f (x)的极限 六、x → x − 0 ( x → x0 − )时,函数 f (x)的极限 三、x →−时,函数 f (x)的极限 四、x → x0 时,函数 f (x)的极限 七、小结与思考

、当x>0时函数的极限 y 考察当x→∞时,函数f(x)=二 的变化趋势 X 1 由图可以看出,当X的绝对值无限增大时, y= X f(x)1 的值无限接近零。 1 →0, X→十00 X x 1 >0, X→-∞ X 1 即:二→0, X→00 X 小作米 ✉合
一、当 x → 时函数的极限 x y 1 = x y O 考察当 x → 时,函数 的变化趋势 x f x 1 ( ) = 0, x → + 1 → x x f (x) 由图可以看出,当 的绝对值无限增大时, 的值无限接近零。 即: 0, x →- 1 → x 0, x → 1 → x

定义1如果当X的绝对值无限增大(即x→∞) 时,函数f(x)无限接近于一个确定的常数A,那么常 数A就叫函数f(x)当x→o时的极限,记作 Iimf(x)=A或f(x)→A(当x→oo) 上述例子可以记为mmf()=m1=0 >00 X→0X
定义 1 如果当 x 的绝对值无限增大(即 x → ) 时,函数 f (x)无限接近于一个确定的常数A,那么常 数A就叫函数 f (x)当x → 时的极限,记作 lim ( ) = ( ) → ( → ) → f x A f x A x x 或 当 0 1 lim ( ) = lim = → → x f x x x 上述例子可以记为

定义2 如果当x→+0时,函数f(x)无限接近于一 个确定的常数A,那么常数A就叫函数f(x)当x→+∞时 的极限,记作 limf(x)=A或记为,f(x)→A(x→+o) x→+00 米吃 ✉合
定义 2 如果当 x → + 时,函数 f (x)无限接近于一 个确定的常数A,那么常数A就叫函数 f (x)当 x → +时 的极限,记作 = 或记为, → ( → +) →+ f x A f x A x x lim ( ) ( )
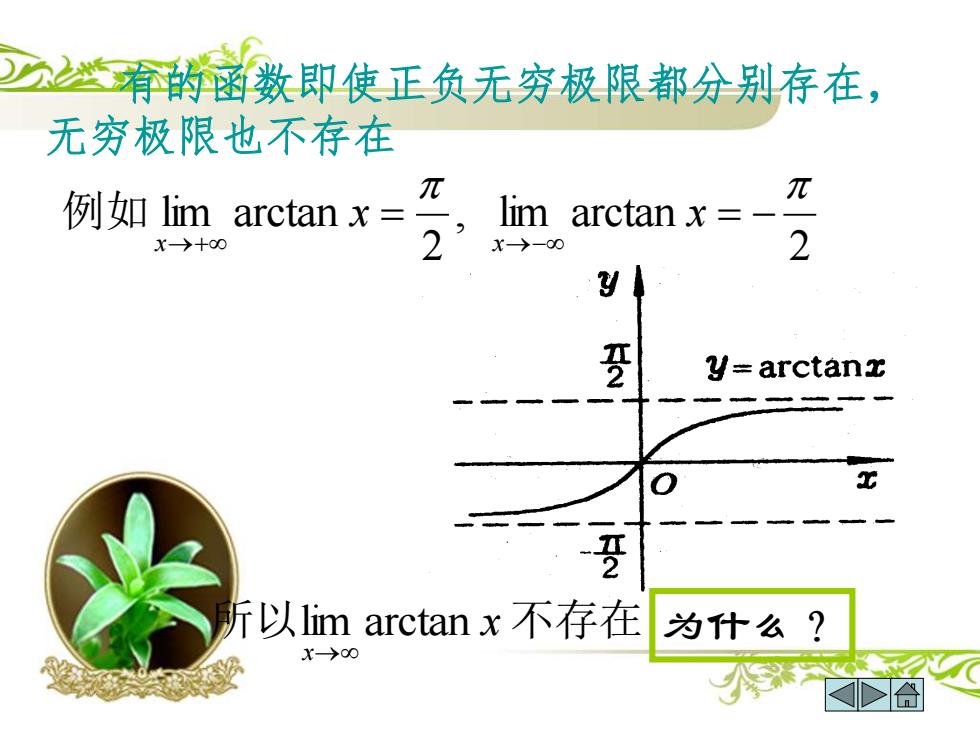
有的函数即使正负无穷极限都分别存在, 无穷极限也不存在 例如lim arctan x= π 元,lim arctan x= π X>+00 2 X>-00 2 罗 y=arctanz 斤以lim arctanx不存在 为什么? X→00 合
, 2 lim arctan = →+ x x 例如 所以 x 不存在 x lim arctan → 为什么? 有的函数即使正负无穷极限都分别存在, 无穷极限也不存在 2 lim arctan = − →− x x