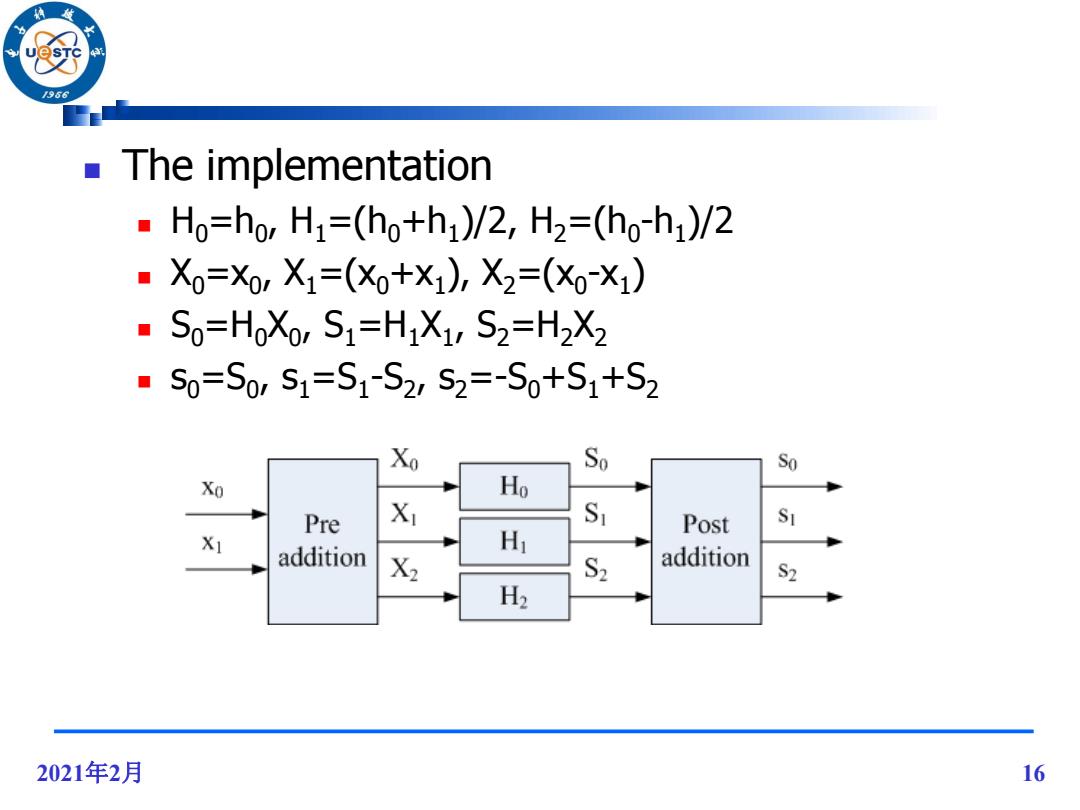
/966 The implementation Ho=hor H1=(ho+h1)/2,H2=(ho-h1)/2 ·X0=X,X1=(X+×1),X2=(X0-X1) So=HoXor S1=HiX1,S2=H2X2 ·s0=S0,S1=S1-S2,S2=-S0+S1+S2 X So So Xo Ho Pre X S Post S1 X1 addition H X2 S2 addition S2 H2 2021年2月 16
2021年2月 16 The implementation H0=h0 , H1=(h0+h1 )/2, H2=(h0 -h1 )/2 X0=x0 , X1=(x0+x1 ), X2=(x0 -x1 ) S0=H0X0 , S1=H1X1 , S2=H2X2 s0=S0 , s1=S1 -S2 , s2=-S0+S1+S2

Comments /96 Some additions in the preaddition or postaddition matrices can be shared.So, when we count the number of additions,we only count one instead of two or three. ■ If we take ho,h as the FIR filter coefficients and take xo,x1 as the signal(data)sequence,then the terms Ho,Hi need not be recomputed each time the filter is used.They can be precomputed once offline and stored.So,we ignore these computations when counting the number of operations. 2021年2月 17
2021年2月 17 Comments Some additions in the preaddition or postaddition matrices can be shared. So, when we count the number of additions, we only count one instead of two or three. If we take h0 , h1 as the FIR filter coefficients and take x0 , x1 as the signal (data) sequence, then the terms H0 , H1 need not be recomputed each time the filter is used. They can be precomputed once offline and stored. So, we ignore these computations when counting the number of operations

Comments /96 ■ We can understand the Cook-Toom algorithm as a matrix decomposition.In general,a convolution can be expressed in matrix-vector forms. Although the number of multiplications is reduced,the number of additions has increased. The Cook-Toom algorithm can be modified in order to further reduce the number of additions. 2021年2月 18
2021年2月 18 Comments We can understand the Cook-Toom algorithm as a matrix decomposition. In general, a convolution can be expressed in matrix-vector forms. Although the number of multiplications is reduced, the number of additions has increased. The Cook-Toom algorithm can be modified in order to further reduce the number of additions

Modified Cook-Toom algorithhm 96 ■( Cook-Toom algorithm is modified in order to further reduce the number of addition operations. Define s'(p)=s(p)-SL+N-2P L+W-2 Notice that the degree of sp)is L+N-2 and S+2 is its highest order coefficient.Therefore the degree of sp)is L+N-3. 2021年2月 19
2021年2月 19 Cook-Toom algorithm is modified in order to further reduce the number of addition operations. Define Notice that the degree of s(p) is L+N-2 and SL+N-2 is its highest order coefficient. Therefore the degree of s'(p) is L+N-3. 2 2 '( ) ( ) L N s p s p sL N p Modified Cook-Toom algorithhm

Steps of modified algorithm 96 Step 1:Choose L+/-2 different real numbers βoβ1βL+N-3 Step 2:Compute hB)and xB)for i=0,...,L+N- 3 a Step3:Compute s(β)=hβ,xβ,)for i=0,..,L+N-3 ■ Step 4:Compute s(B)=s(B)-sL+Np+N-2 ■Step5:Compute s'(p Step 6:Compute s(p)=s(p)+s+Np+W-2 2021年2月 20
2021年2月 20 Steps of modified algorithm Step 1: Choose L+N-2 different real numbers β0 ,β1 ,…,βL+N-3 Step 2: Compute h(βi ) and x(βi ) for i=0,…,L+N- 3 Step 3: Compute s(βi )= h(βi )x(βi ) for i=0,…,L+N-3 Step 4: Compute s’(βi )= s(βi )-sL+N-2p L+N-2 Step 5: Compute s’(p) Step 6: Compute s(p)=s’(p)+ sL+N-2p L+N-2