4.矢量既要有数值大小(包括有关的单位),又要有方向才能完全确定。这些量之间的运算并不遵循一般的代数法则,而遵循特殊的运算法则。这样的量叫做物理矢量。有些物理量,只具有数值大小(包括有关的单位),而不具有方向性。这些量之间的运算遵循一般的代数法则。这样的量叫做物理标量
4.矢量 既要有数值大小(包括有关的单位),又要有方向才能 完全确定。这些量之间的运算并不遵循一般的代数法则, 而遵循特殊的运算法则。这样的量叫做物理矢量。有些物 理量,只具有数值大小(包括有关的单位),而不具有方向 性。这些量之间的运算遵循一般的代数法则。这样的量叫 做物理标量

天量是有大小和方向的。一个失量A可以用它的大小和方向表示为A=αA式中A=A是A的大小(也称为模或长度),而α是沿A方向且大小等于1的无量纲单位矢量(也称A的单位量),因此AAaAAA.通常我们用曲线形象地表示矢量场在空间的分布,其中某处的疏密程度表示该处场量的大小(强弱),而曲线在该点的切线方向则是该点矢量场的方向。这种曲线称为“力线”或“通量线
矢量是有大小和方向的。一个矢量A可以用它的大小 和方向表示为 。式中 ,是A的大小(也称 为模或长度),而aA是沿A方向且大小等于1的无量 纲单位矢量(也称A的单位矢量),因此 A = aA A A = A A A A A A a = = 通常我们用曲线形象地表示矢量场在空间的分布,其 中某处的疏密程度表示该处场量的大小(强弱),而曲线 在该点的切线方向则是该点矢量场的方向。这种曲线称为 “力线”或“通量线

1.2矢量代数一、矢量加法和减法:1、矢量加法:在直角坐标系中:A-a,A, +a,A,+a.A.B=a,B,+a,B,+a,B.A+B=a(A, +B,)+a,(A, +B,)+a(A, +B.)矢量位置矢量p
1.2 矢量代数 一、矢量加法和减法: 1 、矢量加法: 在直角坐标系中: x x y y z Az A a A a A a = + + x x y y z Bz B a B a B a = + + ( ) ( ) ( ) x x x y y y z Az Bz A+ B = a A + B + a A + B + a + 矢量 位置矢量p

矢量的乘法(1)点积(或标量积)B两个量A与B的点积记为A·B。定义为UA·B=A|Bcos(A,B)ABcos 0直角坐标系中的单位失量有下列关系式ax·ay=ayaz=ax·az=0axax=ayay=azaz=1A·B=AxBx+AyBy+Azi量的点积服从乘法交换律和分配律,即A·B=B.AA·B+C=A·B+A·C两个量平行则点积最大,垂直则点积为零
矢量的乘法 AB = A B cos(A,B) A (B C) A B A C A B B A + = + = (1)点积(或标量积) 两个矢量A与B的点积记为A·B。定义为 矢量的点积服从乘法交换律和分配律,即 两个矢量平行则点积最大,垂直则点积为零。 直角坐标系中的单位矢量有下列关系式: ax·ay=ay·az= ax·az=0 ax·ax=ay·ay=az·az=1 A·B=AxBx+AyBy+AzBz Bcos A B
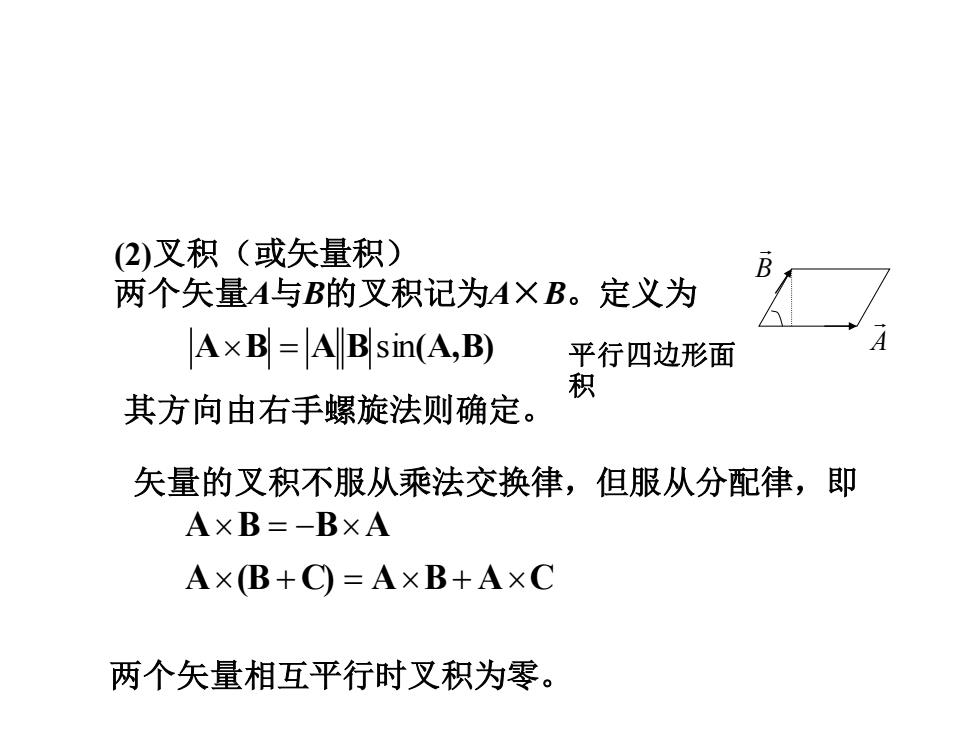
(2)叉积(或矢量积)R两个矢量A与B的又积记为AXB。定义为AxB=ABsin(A,B)平行四边形面积其方向由右手螺旋法则确定。矢量的又积不服从乘法交换律,但服从分配律,即A×B=-B×AA×(B+C)=A×B+A×C两个矢量相互平行时叉积为零
AB = A B sin(A,B) (2)叉积(或矢量积) 两个矢量A与B的叉积记为A×B。定义为 其方向由右手螺旋法则确定。 矢量的叉积不服从乘法交换律,但服从分配律,即 A (B C) A B A C A B B A + = + = − 两个矢量相互平行时叉积为零。 B A 平行四边形面 积