西安毛子科技大学微分中值定理XIDIANUNIVERSITY注意:定理条件条件不全具备,结论不一定成立LVb00boabaf(a) # f(b)f(x)在 xo 不连续f(x)在 xo不可导
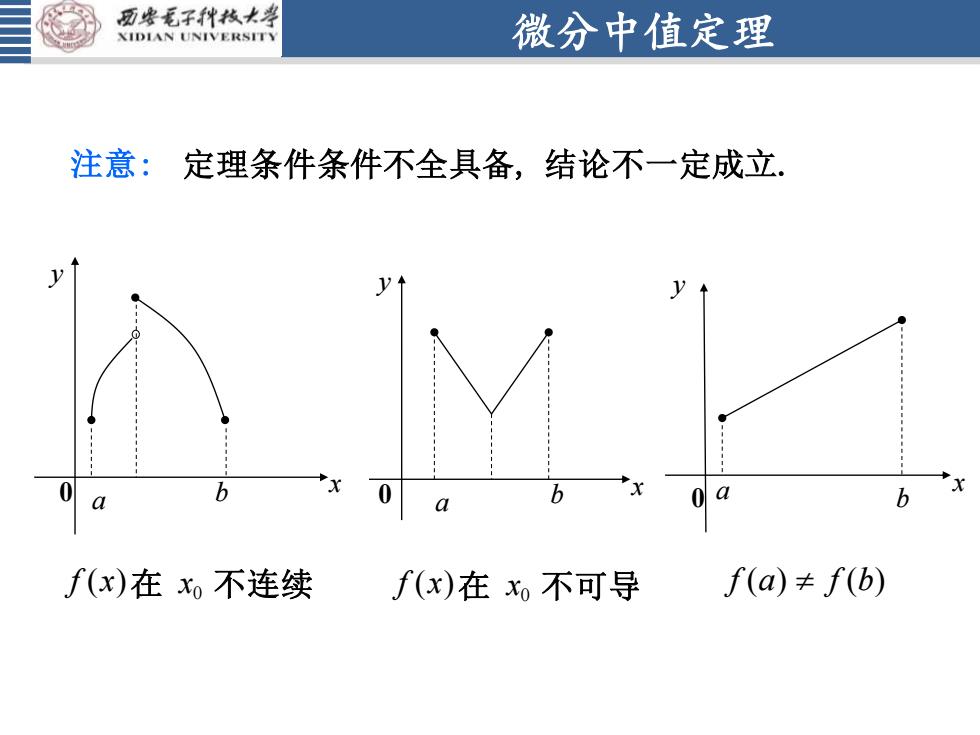
微分中值定理 注意: 定理条件条件不全具备, 结论不一定成立. x y 0 a 0 x b x y 0 a b 0 x a b x y 0 f x( ) 在 x0 不连续 f a f b ( ) ( ) f x( ) 在 x0 不可导

西要毛子科技大学微分中值定理XIDIANUNIVERSIT例1证明方程xs+x-1=0只有一个正根证(存在性)设f(x)=xs +x-1,则f(x)在[0,1]上连续f(1) =1.且,f(0)=-1,由零点定理可知:存在 xE(0,1),使得 f(x)=0即f(x)=0 在(0,+) 内至少有一根
微分中值定理 且 f (0) 1, = − f (1) 1. = 例1 证明方程 只有一个正根. 5 x x + − =1 0 由零点定理可知:存在 x0 (0,1) ,使得 0 f x( ) 0, = 即 f x( ) 0 = 在 (0, ) + 内至少有一根. 证(存在性) 设 则 在 上连续, 5 f x x x ( ) 1, = + − f x( ) [0,1]

西安毛子科技大学微分中值定理XIDIAN UNIVERSITS例1证明方程x+x-1=0只有一个正根证(唯一性)假设另有x E(O,+oo)使 f(x)=f(x)=0因为f(x)在以xo,x为端点的区间满足罗尔定理条件所以在xo,x之间至少存在一点,使f()=0又f(x)=5x4+1>0,矛盾,故假设不真。综上xs+x-1=0只有一个正根
微分中值定理 例1 证明方程 只有一个正根. 5 x x + − =1 0 故假设不真. 因为 f x( ) 在以 x0 , x1 为端点的区间满足罗尔定理条件, 又 矛盾, 4 f x x ( ) 5 1 0, = + 综上 只有一个正根. 5 x x + − =1 0 所以在 x0 , x1 之间至少存在一点 , 使 f ( ) 0, = 证(唯一性) 假设另有 x1 + (0, ) 使 1 0 f x f x ( ) ( ) 0, = =
西安毛子科技大学微分中值定理IDIAN UNIVERSITY三.拉格朗日中值定理定理2(拉格朗日中值定理)如果函数f(x)满足(1)在闭区间[a,b]上连续;y(2)在开区间(a,b)内可导,则在(a,b)内至少存在一点,使得fx(s)= (b)-f(a)0a5b+b-a即 f(b)-f(a)=f'()(b-a)
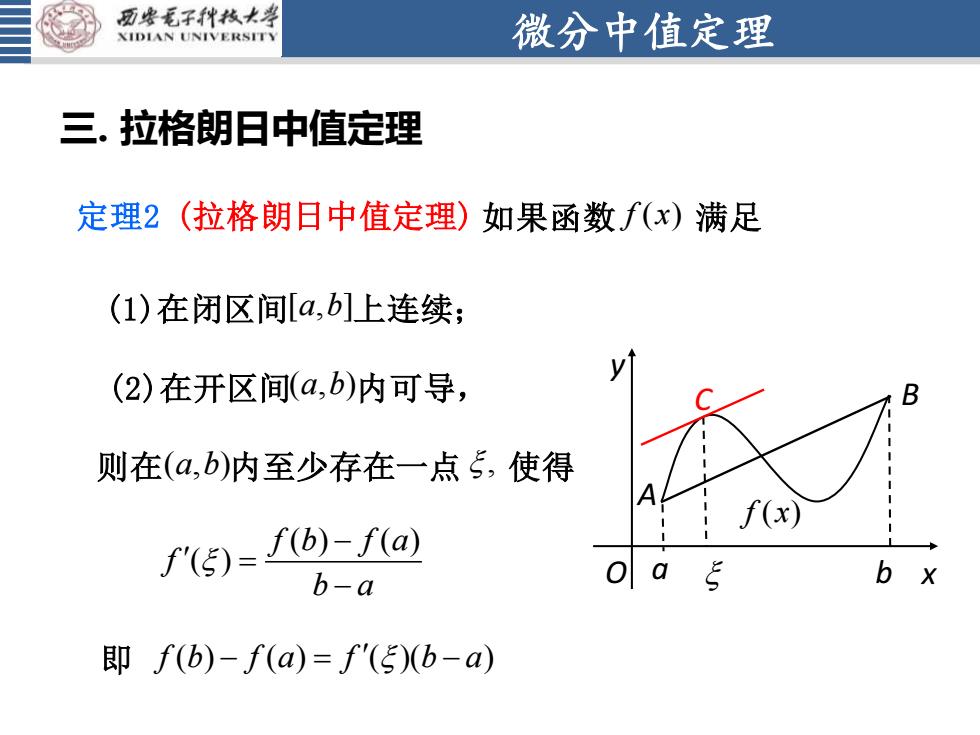
微分中值定理 三. 拉格朗日中值定理 (1)在闭区间 [ , ] a b 上连续; (2)在开区间 ( , ) a b 内可导, 则在 ( , ) a b 内至少存在一点 , 使得 ( ) ( ) ( ) f b f a f b a − = − A B a b x y O C f x( ) 定理2 (拉格朗日中值定理) 如果函数 f x( ) 满足 即 f b f a f b a ( ) ( ) ( )( ) − = −