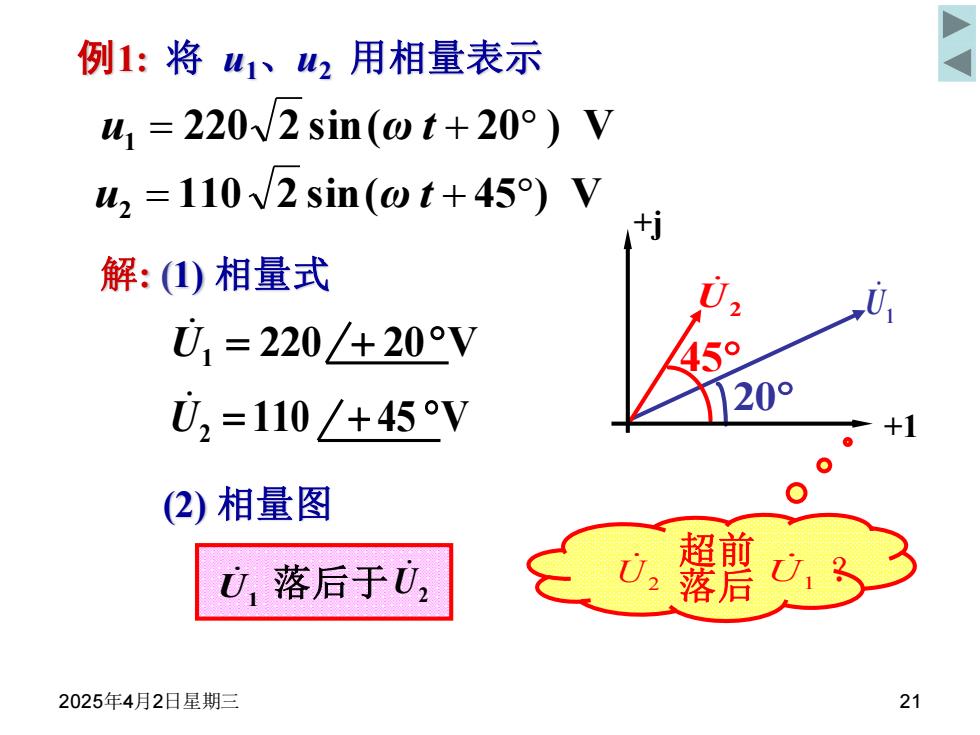
例1:将w1、2用相量表示 41=220W2sin(wt+20°)V u2 =110v2 sin(@t+45)V 解:(1)相量式 01=220/+20V o 02=110/+45V 20° (2)相量图 超前 01落后于0, 2 落后 2025年4月2日星期三 21
2025年4月2日星期三 21 U1 20 U2 45 U2 U1 落后于 U1 U2 超前 落后 ? 解: (1) 相量式 (2) 相量图 例1: 将 u1、u2 用相量表示 u2 = 110 2 sin(ω t + 45) V u1 = 220 2 sin(ω t + 20 ) V +1 +j U 1 = 220 + 20V U 2 = 110 + 45 V

例2:已知i=12.7W2sin(314t+30)A 2=11V2sin314t-60)A 求:i=i+i i1=12.7/30°A i2=11-60°A i=i1+i2=12.730A+11-60°A =12.7(c0s30°+jsin30)A+11(c0s60°-jsin60)A =(16.5-3.18)A=16.8-10.9°A i=16.8√2sin(314t-10.9)A 有效值I=16.8A 2025年4月2日星期三 22
2025年4月2日星期三 22 例2: 已知 = 12.7( cos 30 + jsin 30 )A +11( cos 60 - jsin 60 )A 有效值 I =16.8 A i 1 = 12 .7 2 sin (314 t + 30 )A i 2 =11 2 sin(314 t -60)A i = i 1 + i 2 。 i =16.8 2 sin( 314 t -10.9 ) A 求: I 1 = 12.7 30A I 2 = 11 - 60A I = I 1 + I 2 = 12.7 30A +11 - 60A = (16.5 - j3.18)A = 16.8 -10.9A
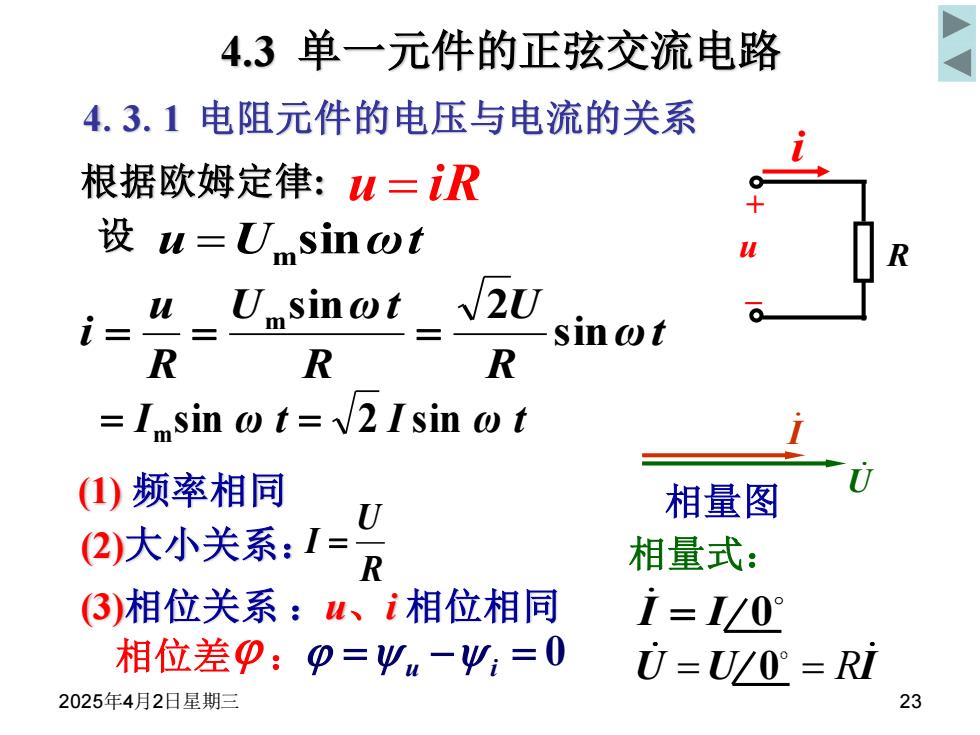
4.3单一元件的正弦交流电路 4.3.1电阻元件的电压与电流的关系 根据欧姆定律:u=iR 设w=Usin ot i= uUmsinot 2U sinωt R R R =Isin @t=2 Isin t ()频率相同 0 相量图 (2)大小关系:1= R 相量式: 3)相位关系:u、i相位相同 i=I/0 相位差P:p=9u-必:=0 U=ULO=Ri 2025年4月2日星期三 23
2025年4月2日星期三 23 设 u =Um sinωt (2)大小关系: R U I = (3)相位关系 :u、i 相位相同 根据欧姆定律: u = iR ωt R U R U ωt R u i sin m sin 2 = = = I sin ω t 2 I sin ω t = m = (1) 频率相同 相位差 : = u - i = 0 I U 相量图 4.3 单一元件的正弦交流电路 R i u + _ 相量式: I = I 0 U U I = = 0 R 4.3.1 电阻元件的电压与电流的关系
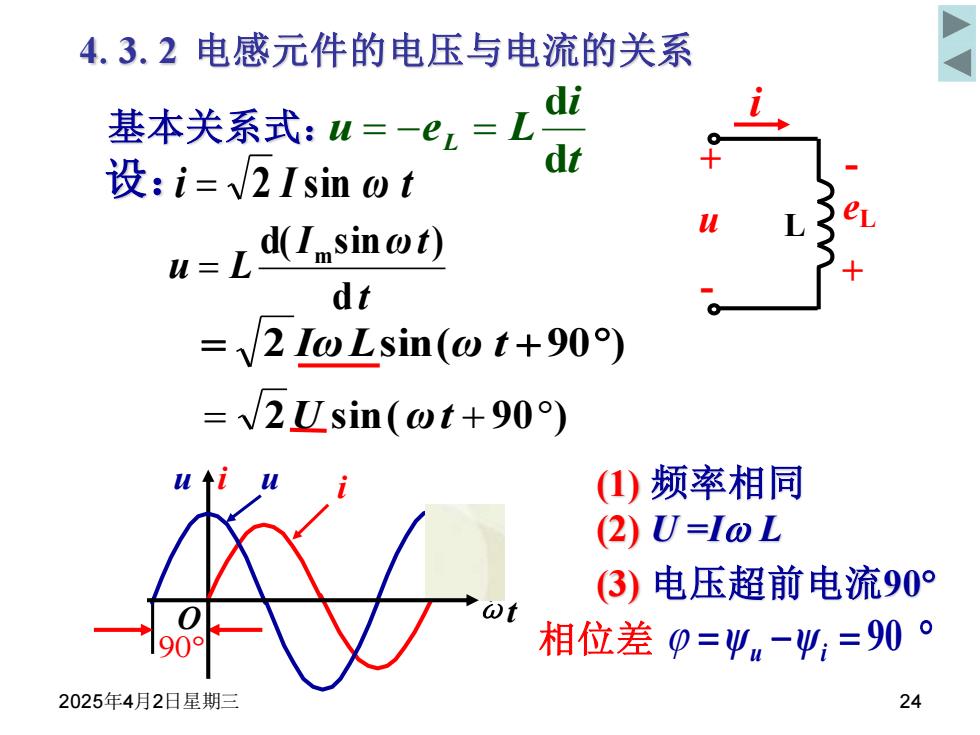
4.3.2电感元件的电压与电流的关系 di 基本关系式:w=-e,=L 设:i=√2 Isin o t u=Ld(Lnsinot) dt =/2 Io Lsin(ωt+90) =√2☑sin(wt+90) (1)频率相同 (2)U=Io L (3)电压超前电流90° 90° 相位差 0=n-4:=90o 2025年4月2日星期三 24
2025年4月2日星期三 24 = 2 IωLsin(ω t + 90) 基本关系式: (1) 频率相同 (2) U =I L (3) 电压超前电流90 = - = 90 90 相位差 ψu ψi t i u eL L d d = - = 4.3.2 电感元件的电压与电流的关系 设: i = 2 I sin ω t i u + - eL + - L t I ωt u L d d( sin ) m = = 2U sin(ωt + 90) u ωt u i i O

{1-anm 有效值:U=I·wL 或I= @L 定义: X,=0L=2πfL 感抗(2) 则: U=IX X2=2元L 直流:∫=0,X,=0,电感L视为短路 交流:f1→X1 电感L具有通直阻交的作用 2025年4月2日星期三 25
2025年4月2日星期三 25 u = 2I ω Lsin (ωt + 90 ) i = 2I sinωt 或 L U I = XL 则: U = I 感抗(Ω) 电感L具有通直阻交的作用 直流:f = 0, XL =0,电感L视为短路 定义: XL =L = 2 f L XL = 2 π fL 有效值: U = I ω L 交流:f XL