
可得:e"=cosy+jsin y 3)指数式A=rejw (4极坐标式A=以必 A=a+ib=rcosu+jrsinw=re =必 相量:表示正弦量的复数称为相量 设正弦量:u=Usin(ωt+) 相量表示: U=Ue"=ULy 相量的模=正弦量的有效值 相量辐角=正弦量的初相角 电压的有效值相量 2025年4月2日星期三 16
2025年4月2日星期三 16 (3) 指数式 ψ A r j = e ψ ψ ψ e cos jsin j 可得: = + sin( ) 设正弦量: u =Um ωt +ψ 相量: 表示正弦量的复数称为相量 电压的有效值相量 A a b r jr r r ψ ψ = + = + = = j j cos sin e (4) 极坐标式 A = r ψ 相量表示: 相量的模=正弦量的有效值 相量辐角=正弦量的初相角 U Ue U ψ ψ = = j
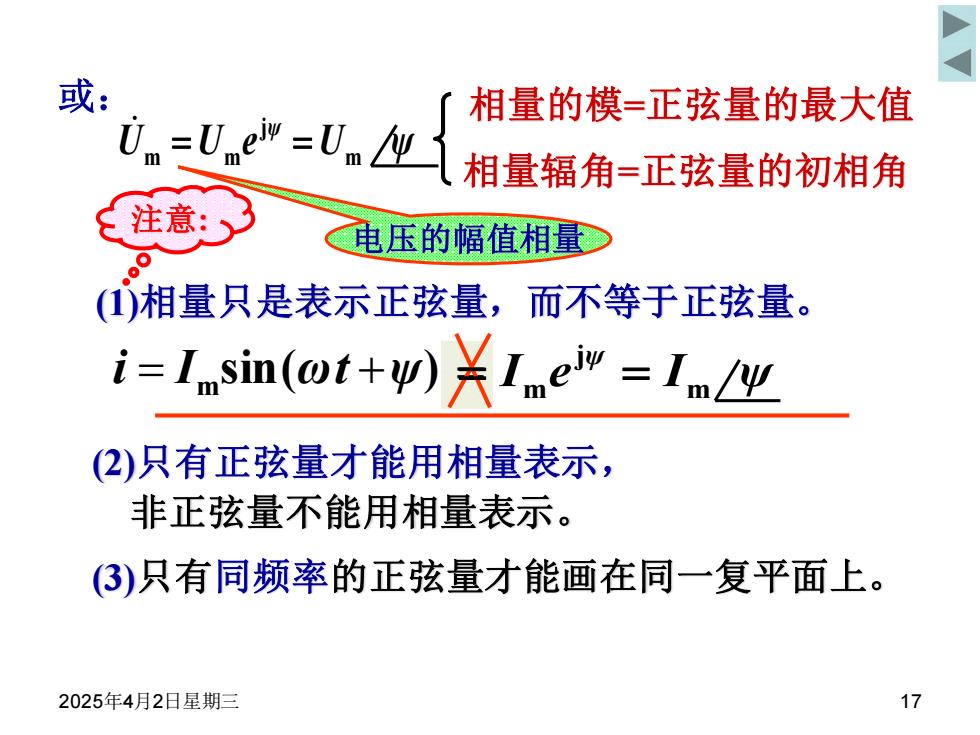
或: 相量的模=正弦量的最大值 0m=Unew=Um 相量辐角=正弦量的初相角 注意:) 电压的幅值相量 (少相量只是表示正弦量,而不等于正弦量。 i=Insin(ot+p)关Ime形=Imy (2)只有正弦量才能用相量表示, 非正弦量不能用相量表示。 (3)只有同频率的正弦量才能画在同一复平面上。 2025年4月2日星期三 17
2025年4月2日星期三 17 电压的幅值相量 (1)相量只是表示正弦量,而不等于正弦量。 注意: sin( ) i = I m ωt +ψ ?= (2)只有正弦量才能用相量表示, 非正弦量不能用相量表示。 (3)只有同频率的正弦量才能画在同一复平面上。 相量的模=正弦量的最大值 相量辐角=正弦量的初相角 U U e U ψ ψ m j m m = = 或: I e I ψ ψ m j = m =

(4)相量的两种表示形式 相量式:U=Ue"=U/y=U(cosw+jsin) 相量图:把相量表示在复平面的图形 可不画坐标轴 (⑤)相量的书写方式 ·模用最大值表示,则用符号: Um/m ·实际应用中,模多采用有效值,符号: 0、i 如:已知u=220sin(wt+45)V 则0m=220esV或i=220 /2 2025年4月2日星期三 18
2025年4月2日星期三 18 (5)相量的书写方式 • 模用最大值表示 ,则用符号: Um I m 、 (4)相量的两种表示形式 相量图: 把相量表示在复平面的图形 • 实际应用中,模多采用有效值,符号: U I 、 可不画坐标轴 如:已知 u = 220 sin(ω t + 45)V 220e V j45 m U = e V 2 220 j45 则 或 U = e (cos jsin ) j U U U ψ U ψ ψ ψ = = = + 相量式: I U

(6)旋转因子e 电旋转因子e=1∠0是一个模 等于1,辐角为0的复数。 任意一个复数A=4e乘以 e,等于把A逆时针旋转0 +1 角度,而模4保持不变。 0 e贤=j AXj=jA,等于把A 逆时针旋转90°。 =j 都是旋 转因子 ej远=-1 月=,等于把4 顺时针旋转90。 2025年4月2日星期三 19
2025年4月2日星期三 19 (6) 旋转因子e jq 旋转因子 e jq =1∠q是一个模 等于1,辐角为q的复数。 任意一个复数A=|A|e jqa乘以 e jq ,等于把A逆时针旋转q 角度,而模|A|保持不变。 +j o +1 A qa Ae jq q 都是旋 转因子 A×j = jA,等于把 A 逆时针旋转90o 。 = -jA,等于把 A A j 顺时针旋转90o 。 e 2 = j j e 2 = -j -j e j = -1
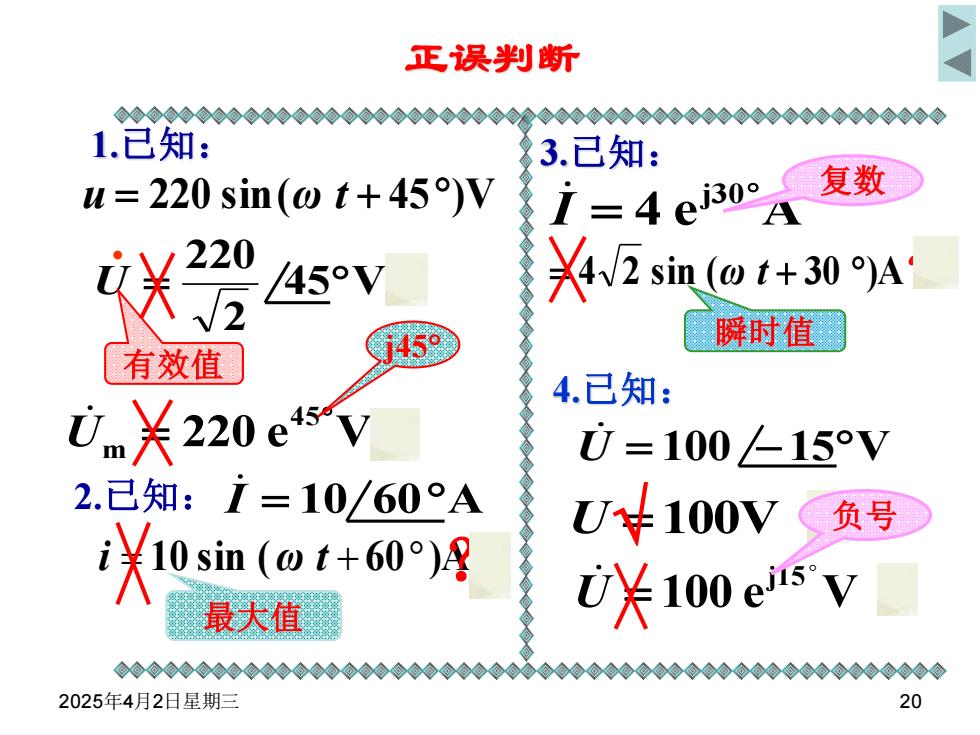
正误判断 ◇◇◇⊙⊙◆◇◇⊙◆0◇⊙⊙0⊙◇0◆⊙0⊙@ 0⊙0⊙@0◇◇0⊙◇◇⊙⊙0◆◆0◆⊙0⊙00@ 1.已知: 3.已知: u=220 sin(@t+45)V i=4e30°A 复数 45V 42 sin (1+30)A j45 瞬时值 有效值 4.已知: 0nm关220e4sV U=100/-15V 2.已知:1=10/60°A U+100V 负号 关0sim(at+609 最大值 0米100es'V 2025年4月2日星期三 20
2025年4月2日星期三 20 45 V 2 220 U = ? 正误判断 1.已知: u = 220 sin(ω t + 45)V 220 e V 45 m U = ? 有效值 = 4 2 sin (ω t + 30 )A ? 4 e A j30 I = 3.已知: 复数 j45 瞬时值 • i = 10 sin (ω t + 60)A ? 最大值 U = 100V ? 100 e V j15 U = ? 负号 2.已知: I = 10 60A 4.已知: U = 100 -15V