
第1章检测技术的基本概念■15 的误差。从图1-5中还可以看出,一系列测量值与x的差值就是随机误差,它们与真值的差 值等于随机误差加上系统误差。 (2)对称性x,大致对称地分布于x两侧。我们将x,与x之差称为剩余误差,也称残差V V=x-x (1-7) 从图15还可以看出,在x两侧的残差V基本上相互抵消 ∑y=y+2+…+V.一0 所以凡具有抵消性的误差,一般可按随机误差处理。 (3)有界性在一定的条件下,x,有一定的分布范围,超过这个范围的可能性非常小, 即出现绝对误差很大的情况很少。 除此之外,进一步分析可以证明,当n→时,测量列x的算术平均值x可以认为是测 量值的最可信值,或者也可以说是数学期望值(Mathematical Expectation)。但是,在有随机 误差存在的情况下,只使用x仍无法表达出测量值的误差范围和准确度的高低。 在工程测量中,一般用下式表示存在随机误差时的测量结果 x=x±△x (1-8) △x表示测量值的误差范围。根据统计学原理,常采用3石准则,工程上常令 =3=3√nn- (1-9) 式(1-9)中,石称为算术平均值的方均根误差,过去也称为算术平均值的标准差。σ 可用下式计算 g= (1-10) n(n-1) 由于云与n有关,n越大,测得的σ就越小,即测量的准确度就越高。但是增加测量次 数必须付出较多的时间,科学家贝塞尔经大量的实验证明,当>I0时,。的减小就非常缓 慢,因此在一般情况下,n略大于10即可。 由于测量过程中还可能存在粗大误差,必须予以剔除。在误差理论中,还规定了一个评 定单次测量结果离散性大小的标准,称为方均根误差:(请注意它与石的区别) G=n -1 (1-11) 根据拉依达准则,当测量次数n>10且测量列x符合正态分布时,残差V超过3σ的可 能性只有0.3%,它的置信度为99.7%。因此,可以用方均根误差来检查测量结果中是否存 在粗大误差,残差超过3σ(极限误差)的测量值称为坏值,应予以剔除。 由式(1-10)和式(1-11)可知,算术平均值的方均根误差G与方均根误差σ的关系是 G=σ/n,因此,测量结果x也可用下式表示 x=x±3=元±3 (1-12)
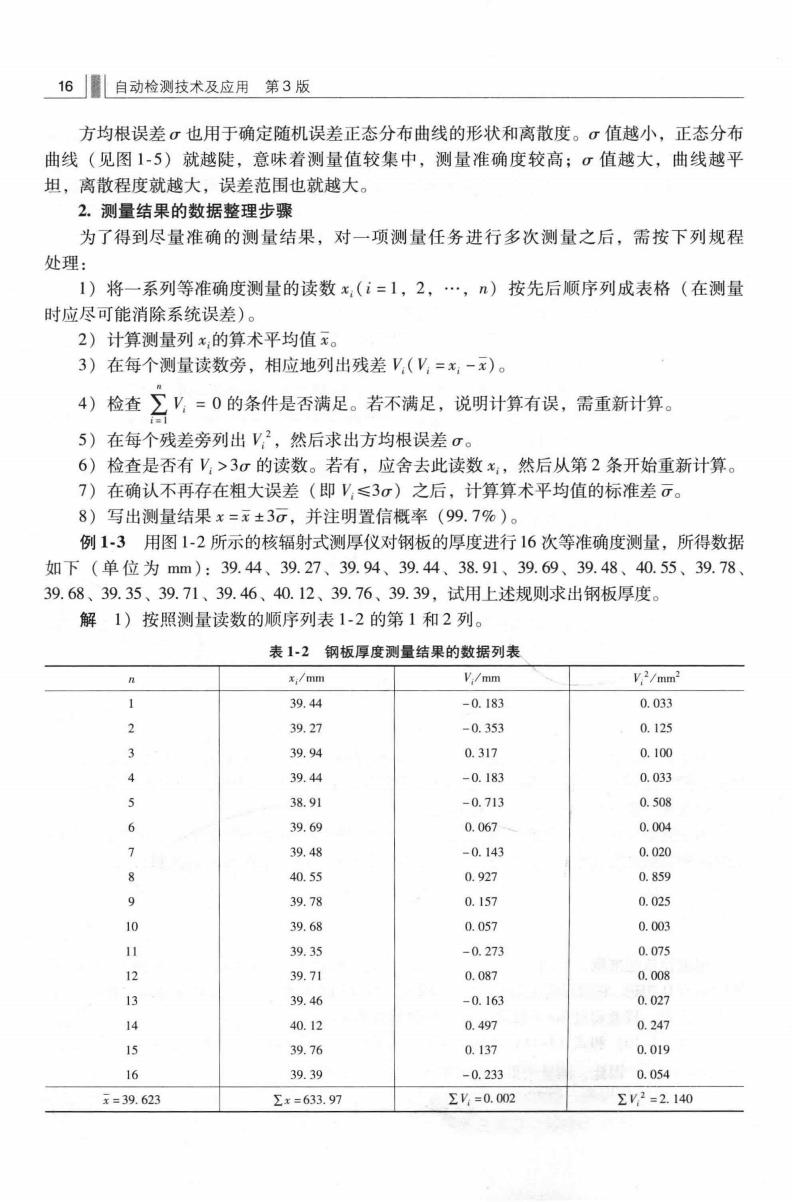
16■自动检测技术及应用第3版 方均根误差σ也用于确定随机误差正态分布曲线的形状和离散度。σ值越小,正态分布 曲线(见图15)就越陡,意味着测量值较集中,测量准确度较高;σ值越大,曲线越平 坦,离散程度就越大,误差范围也就越大。 2。测量结果的数据整理步骤 为了得到尽量准确的测量结果,对一项测量任务进行多次测量之后,需按下列规程 处理: 1)将一系列等准确度测量的读数x,(i=1,2,…,)按先后顺序列成表格(在测量 时应尽可能消除系统误差)。 2)计算测量列x的算术平均值x。 3)在每个测量读数旁,相应地列出残差V,(V=x,-x)。 4)检查∑V,=0的条件是否满足。若不满足,说明计算有误,需重新计算。 5)在每个残差旁列出V2,然后求出方均根误差σ。 6)检查是否有V>3σ的读数。若有,应舍去此读数x,然后从第2条开始重新计算 7)在确认不再存在粗大误差(即V,≤3σ)之后,计算算术平均值的标准差G。 8)写出测量结果x=±3,并注明置信概率(99.7%)。 例13用图1-2所示的核辐射式测厚仪对钢板的厚度进行16次等准确度测量,所得数据 如下(单位为mm):39.44、39.27、39.94、39.44、38.91、39.69、39.48、40.55、39.78 39.68、39.35、39.71、39.46、40.12、39.76、39.39,试用上述规则求出钢板厚度。 解1)按照测量读数的顺序列表1-2的第1和2列。 表12钢板厚度测量结果的数据列表 x./mm V./mm V2/mm2 39.44 -0.183 0.033 39.27 -0.353 0.125 39.94 0.317 010 4 39.44 -0.183 0.033 5 38.91 -0.713 0.508 6 39.69 0.06 0.00 39.48 -0.143 0.020 40.55 092 Q859 39.78 0.157 0.025 10 39.68 .057 0.00 11 39.35 -0.273 0.075 39.71 0.087 a.08 13 39.46 -0.163 0.027 14 40.12 0.497 0.247 15 39.76 013 0.019 16 39.39 -0.233 0.054 x=39.623 Σx=633.97 Σ=0.002 Σ2=2.140

第1章检测技术的基本概念」顺L17 2)计算测量列x,的算术平均值:x=(633.97/16)mm=39.623mm。 3)在测量值x,右边写出残差V,验证∑V=0,并填写到表1-2的第3列。 4)在每个残差的右边列出计算σ和。所必须的中间过程值V2,并填写到表1-2的第4 列,计算出∑V2=2.140mm2。 5)计算方均根误差:0=√只-=0.378mm 6)计算极限误差30=1.134mm。经检查,未发现V>3o,故16个测量值中均无坏值 7)计算算术平均值的标准差:了一层=0095mm。 8)写出测量钢板厚度的结果:x=元+30=39.62mm±0.29mm(99.7%)。 在上述计算过程中,由于测量列x,小数点后只有两位,因此各个中间值需在小数点后保 留3位,最后结果只能保留小数点后两位。 以上复杂的数据整理步骤需要编制程序,利用计算机来完成。 3.不确定度的基本概念及不确定度报告 在实际测量中,除了上述3G的概念之外,还应考虑测量不确定度(Measurement Uncer-- taiy)的影响。测量结果仅仅是被测量的一个估计值,因此测量结果必然带有不确定性 不确定性越大,测量结果的质量就越差。测量不确定度的含义是指:由于测量误差的存在, 对被测量值的“不能肯定的程度”,也表明该结果的可信赖程度。不确定度是测量结果质量 的指标)。不确定度越小,所述结果与被测量的真值越接近。在报告测量结果时,必须 给出相应的不确定度,便于使用该测量结果的人评定其可靠性。测量不确定度包含A类评 定和B类评定。在完成不确定度的分析和评定后,应给出不确定度报告。 4.测量系统静态误差的合成 一个测量系统一般由若干个单元组成,这些单元在系统中称为环节。为了确定整个系统 的静态误差,需将每一个环节的误差综合起来,称为误差的合成。 由n个环节串联组成的开环系统如图16所示。输人量为x,输出量y。=f八x) □”2为3,1m名 图16由n个环节串联组成的开环系统 若第i个环节的满度相对误差为y,时,则输出端的满度相对误差y。与y,之间的关系可 用以下两种方法确定: (1)绝对值合成法绝对值合成法是从最不利的情况出发的合成方法,即认为在个 分项y,中有可能同时出现正值或同时出现负值,则总的合成误差为各环节误差Y,的绝对值 之和,即 ya=∑y=±(yl+ly2+…+ly.l) (1-13) 这种合成法对误差的估计是偏大的,因为每一个环节的误差实际上不可能同时出现最大

18自动检测技术及应用第3版 值,精确的方法必须考虑各个环节误差可能出现的概率。 (2)方均根合成法当系统误差的大小和方向都不能确切掌握时,可以仿照处理随机 误差的方法来处理系统误差。计算公式为 =±√y+y+…+y (1-14) 例14用图12所示的核辐射式钢板测厚仪测钢板厚度,已知y射线检测管的测量误 差为±5%,微电流放大器误差为±2%,指针表误差为±1%,求测量的总误差。 解(1)用绝对值合成法计算测量误差 ym=±(y,|+|y2+…+ly.)=±(5%+2%+1%)=±8% (2)用方均根合成法 m =±/(59%)2+(2%)2+(1%)2✉±5% 用方均根合成法估算测量的总误差较为合理。从本例中还可以看到,测量系统中的一个 或几个环节的准确度特别高,对提高整个测量系统总的准确度意义不大,反而提高了测量系 统的成本,造成了资源浪费。例如在本例中,如果一味提高显示仪表的准确度并不能有效地 减小测量总误差,而应努力提高误差最大的某个环节的测量准确度。在这里,传感器(γ射 线管)的误差最大,应选购更高一级的传感器,以达到最佳的性能价格比。 1.3传感器及其基本特性 1.3.1传感器定义及组成 1.3拓展阅读资料 传感器是一种检测装置,能感受规定的被测量,并能将检测感受 到的信息按一定规律变换成电信号或其他可用信号,以满足信息的传输、处理、存储、显 示、记录和控制等要求,它是实现自动检测和自动控制的重要环节,有时也可以称为换能 器、检测器、探头等。大部分传感器由敏感元件、传感元件及测量转换电路三部分组成,如 图17所示。 液油然般练元件☐事电量一传塔元件☐电参量测量转换电路电量 图17传感器组成框图 图17中的敏感元件在传感器中直接感受被测量的元件,被测量通过敏感元件转换成与 被测量有确定关系、更易于转换的非电量(某些传感器的敏感元件能够直接输出电参量)。 这一非电量通过传感元件后被转换成电参量。测量转换电路的作用是将传感元件输出的电参 量转换成易于处理的电压、电流或频率量。应该指出,不是所有的传感器都有敏感元件、传 感元件之分,有些传感器是将两者合二为一了。 电位器式压力传感器示意图如图1-8所示。当被测压力增大时,弹簧管撑直,通过齿 条带动齿轮转动,从而带动电位器的电刷产生角位移。电位器电阻的变化量反映了被测压力 P值的变化。在这个传感器中,弹簧管为敏感元件,它将压力转换成角位移α。电位器为传 感元件,它将角位移转换为电参量 一电阻的变化△R。当电位器的两端加上电源后,电位 器就组成分压比电路,它的输出量是与压力成一定关系的电压0。在这个例子中,电位器

第1章检测技术的基本概念圆19 又属于分压比式测量转换电路。 b) 图1-8电位器式压力传感器示意图 a)原理示意图b)外形图 1一弹簧管(敏感元件)2一电位器(传感元件,测量转换电路)3一电刷4一传动机构(齿轮-齿条) 结合上述工作原理,可将图18框中的内容具体化,可画出电位器式压力传感器原理框 图,如图1-9所示。 角电位国电分比电出电 图19电位器式压力传感器原理框图 1.3.2传感器分类 传感器的种类名目繁多,分类不尽相同。常用的分类方法有: 1)按被测量分类:可分为位移、力、力矩、转速、振动、加速度、温度、压力、流 量、流速等传感器。 2)按测量原理分类:可分为电阻、电感、电容、压电、超声波、热电偶、激光、红 外、光导纤维、光栅、磁栅、容栅等传感器。 3)按传感器输出信号的性质分类:可分为输出为开关量(“1”和“0”或“开”和 “关”)的开关型传感器;输出为模拟量的模拟型传感器,输出为脉冲或代码的数字型传 惑器。 1.3.3传感器的基本特性 传感器的特性一般指输人和输出特性,它有静态和动态之分。传感器动态特性的研究方 法与控制理论中介绍的相似,本书仅介绍传感器静态特性的一些重要指标。 1.灵敏度 灵敏度(Sensitivity)是指传感器在稳态下输出变化值与输入变化值之比,用K表 示。即 (1-15) 式中x—输入量: 输出量。 对线性传感器而言,灵敏度为一常数;对非线性传感器而言,灵敏度随输入量的变化而