
第三章动态电路—灵 3.1动态元件 3.5一阶电路的三要素法 一、电容 一、三要素法公式◆ 电感 、电容电感的串联与 二、 三要素公式说明◆ 3.2动态电路方程及其解 三、三要素的计算 电路方程 四、举例→ 微分方程的经典解 3.6一阶电路的阶跃响应 3.3电路的初始值 一、阶跃函数 换路定律◆ 二、阶跃响应 初始值的求解→ 3.7二阶电路分析 3.4电路的响应 一、RLC串联电路的方程 零输入响应 二、RLC串联电路的零输入响应 零状态响应◆ 三、RLC串联电路的阶跃响应 三、全响应 3.8正弦激励下一阶电路的响 应 点击日录心,进入相关章节
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 3.5 一阶电路的三要素法 一、三要素法公式 二、三要素公式说明 三、三要素的计算 四、举例 3.6 一阶电路的阶跃响应 一、阶跃函数 二、阶跃响应 3.7 二阶电路分析 一、RLC串联电路的方程 二、RLC串联电路的零输入响应 三、RLC串联电路的阶跃响应 3.8 正弦激励下一阶电路的响 应 3.1 动态元件 一、电容 二、电感 三、电容电感的串联与并联 3.2 动态电路方程及其解 一、电路方程 二、微分方程的经典解 3.3 电路的初始值 一、换路定律 二、初始值的求解 3.4 电路的响应 一、零输入响应 二、零状态响应 三、全响应 点击目录 ,进入相关章节 第 3-1 页 前一页 下一页 退出本章 目录

动疮电路 动态元件 许多实际电路,除了电源和电阻外,还常包含电容和电感 元件。这类元件的VCR是微分或积分关系,故称其为动态元件。 含有动态元件的电路称为动态电路,描述动态电路的方程是微分 方程。 一、电容 电容元件(capacitor)是一种储存电能的元件,它是实际电容器 的理想化模型。其电路待号如图所示。 u 1、电容的一般定义 一个二端元件,若在任一时刻t,其电荷()与电压(t)之间的 关系能用山平面上的曲线表征,即具有代数关系∫(山,q)=0 则称该元件为电容元件,简称电容
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第三章 动态电路 许多实际电路,除了电源和电阻外,还常包含电容和电感 元件。这类元件的VCR是微分或积分关系,故称其为动态元件。 含有动态元件的电路称为动态电路,描述动态电路的方程是微分 方程。 电容元件(capacitor)是一种储存电能的元件, 它是实际电容器 的理想化模型。其电路符号如图所示。 u i +q C -q 第 3-2 页 前一页 下一页 返回本章目录 1、电容的一般定义 一个二端元件,若在任一时刻t,其电荷q(t)与电压u(t)之间的 关系能用q~u平面上的曲线表征,即具有代数关系 f (u,q ) = 0 则称该元件为电容元件,简称电容
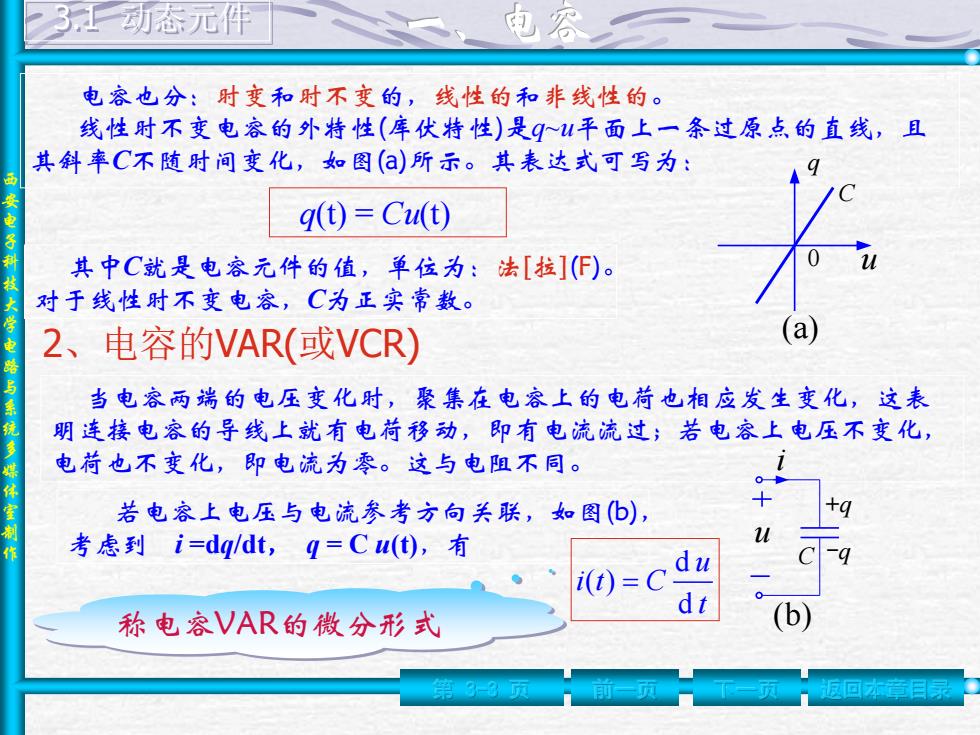
3动态元件 南容 电容也分:时变和时不变的,线性的和非线性的。 线性时不变电容的外特性(库伏特性)是q平面上一条过原点的直线,且 其斜率C不随时间变化,如图()所示。其表达式可写为: 安电 q(t)=Cu(t) 其中C就是电容元件的值,单位为:法[拉](F)。 对于线性时不变电容,C为正实常数。 2、电容的VAR(或VCR) (a) 当电容两端的电压变化时,聚集在电容上的电荷也相应发生变化,这表 明连接电容的导线上就有电荷移动,即有电流流过;若电容上电压不变化, 电荷也不变化,即电流为零。这与电阻不同。 若电容上电压与电流参考方向关联,如图(b), 考虑到i=dq/dt,q=Cu(),有 d u C-c i(t)= d 称电容VAR的微分形式 (b)
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 3.1 动态元件 电容也分:时变和时不变的,线性的和非线性的。 线性时不变电容的外特性(库伏特性)是q~u平面上一条过原点的直线,且 其斜率C不随时间变化,如图(a)所示。其表达式可写为: q(t) = Cu(t) 其中C就是电容元件的值,单位为:法[拉](F)。 对于线性时不变电容,C为正实常数。 (a) q 0 u C 2、电容的VAR(或VCR) 当电容两端的电压变化时,聚集在电容上的电荷也相应发生变化,这表 明连接电容的导线上就有电荷移动,即有电流流过;若电容上电压不变化, 电荷也不变化,即电流为零。这与电阻不同。 若电容上电压与电流参考方向关联,如图(b), 考虑到 i =dq/dt, q = C u(t),有 u i +q C -q (b) t u i t C d d ( ) 称电容VAR的微分形式 第 3-3 页 前一页 下一页 返回本章目录

31上 动态元件 对电容伏安关系的微分形式从-∞到t进行积分,并设一∞)=0,可得 称电容VAR的积分形 u0=5)d5 式 设t=t为初始观察时刻,上式可改写为 u0=5d5+J⑤d5=o)+J(5)d5 ,t2t0 式中 (9)d5 u与i u(to)=- 非关 称为电容电压在to时刻的初始值(initial value),或初始状态 联 (initial state),它包含了在to以前电流的“全部历史”信息8+ 一般取to=0。 若电容电压、电流的参考方向非关联,如右图所示。 电容VAR表达式可改为 i()=-C 0)=)d5=to)乙J5)dE ,t2t0
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 3.1 动态元件 对电容伏安关系的微分形式从-∞到t进行积分,并设u(-∞)=0,可得 t i C u t ( ) d 1 称电容VAR的积分形 ( ) 式 设t=t0为初始观察时刻,上式可改写为 t t t t t i t t C i u t C i C u t 0 0 0 0 0 ( ) d , 1 ( ) d ( ) 1 ( ) d 1 ( ) 0 ( ) d 1 ( ) 0 t i C u t 称为电容电压在t0时刻的初始值(initial value),或初始状态 (initial state),它包含了在t0以前电流的“全部历史”信息。 一般取t0 =0 。 式中 第 3-4 页 前一页 下一页 若电容电压、电流的参考方向非关联,如右图所示。 电容VAR表达式可改为 u i C t u i t C d d ( ) t t t i t t C i u t C u t 0 0 0 ( ) d , 1 ( ) d ( ) 1 ( ) u与i 非关 联 返回本章目录

3,动态元佣 3、电容的功率与储能 当电容电压和电流为关联方向时,电容吸收的瞬时功率为: du(t) p(0)=(00=C0 安 dt 电 电容是储能元件,它不消耗能量。当p(t)>0时,说明电容是 在吸收能量,处于充电状态;当()<0时,说明电容是在释放 能量,处于放电状态。释放的能量总也不会超过吸收的能量。 电容不能产生能量,因此为无源元件。 对上式从一∞到t进行积分,即得t时刻电容上的储能为: wc0=∫ps)d5=OCa(5d(⑤) =号Cu20)-}cw2(-o) 式中u(∞)表示电容未充电时刻的电压值,应有(∞)=0。 于是,电容在时刻1的储能可简化为: w.(=C 可见:电容在某一时刻1的储能仅取决于此时刻的电压,而与电流无 关,且储能≥0
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 3.1 动态元件 当电容电压和电流为关联方向时,电容吸收的瞬时功率为: 3、电容的功率与储能 dt du t p t u t i t Cu t ( ) ( ) ( ) ( ) ( ) 电容是储能元件,它不消耗能量。当 p(t)>0时,说明电容是 在吸收能量,处于充电状态;当 p(t) <0时,说明电容是在释放 能量,处于放电状态。释放的能量总也不会超过吸收的能量。 电容不能产生能量,因此为无源元件。 对上式从-∞到 t 进行积分,即得t 时刻电容上的储能为: ( ) 2 1 ( ) 2 1 ( ) ( ) ( ) ( ) 2 2 ( ) ( ) Cu t Cu w t p d Cu du t u t u C 式中 u(-∞) 表示电容未充电时刻的电压值,应有u(-∞) =0。 于是,电容在时刻 t 的储能可简化为: ( ) 2 1 ( ) 2 wC t Cu t 可见:电容在某一时刻 t 的储能仅取决于此时刻的电压,而与电流无 关,且储能 ≥0。 第 3-5 页 前一页 下一页 返回本章目录