
10自动检测技术及应用第3版 1.2测量误差及数据处理 测量的目的是希望通过测量求取被测量的真值(True Value)。在 一定条件下,任何一个被测量的大小都有一个客观存在的实际值,称 为真值。真值是一个可以接近却难以达到的理想概念。测量的目的就 是要得到被测量的真值,但由于受测量方法、测量仪器、测量条件以 及观测者水平等多种因素的限制,只能获得该物理量的近似值。 1.2拓展阅读资料 真值有理论真值、约定真值(Conventional True Value)和相对真值(Relatively True Vaue)之分。例如,平面三角形的三个内角之和为180°,这种真值称为理论真值。又如,国 际科学与技术数据委员会(C0DATA)1986年推荐的阿伏伽德罗常数为6.022×10mol-': 在标准条件下.水的三相点为273.16K.金的疑周点是1064.18C:米是光在直容中,在 1/299792458s时间间隔内运行路程的长度等,这类真值称为约定真值。准确度高2级或几级 的仪表的误差与准确度低的仪表的误差相比,前者的误差是后者的1/3以下时,则高一级仪 表的测量值可以认为是相对真值。相对真值在误差测量中的应用最为广泛。测量值与真值之 间的差值称为测量误差(Measuring Error)。测量误差可按其不同特征进行分类。 1.2.1测量误差 1.测量误差的表示方法 (1)绝对误差 一个被测量值A,与真值A。之间总是存在着一个差值,这种差值称为绝 对误差(Absolute Error),用△表示,即 △=A-A。 (1-1) 在实验室和计量工作中,常用修正值C表示,即 C=A-A.=-△ (1-2) 由式(1-2)可知,由修正值C、被测量值A,可求得真值A,。绝对误差与被测量的量纲 相同。 (2)相对误差绝对误差不足以反映测量值偏离真值程度的大小,所以引入了相对误 差(Relative Error)。相对误差用百分比的形式来表示,一般多取正值。相对误差可分为示 值相对误差和引用相对误差等。 1)示值(标称)相对误差y,:示值相对误差(Nominal Relative Error)y,用绝对误差△ 与被测量A,的百分比来表示 .=×10% (1-3) 2)引用误差y。:引用误差(Quoted Error)有时也称满度相对误差,用测量仪表的绝 对误差△与仪器满度值A.的百分比来表示 Y=2×100% (1-4) 对测量下限不为零的仪表而言,在式(1-4)中,用量程(A-A)来代替分母中 的An

第1章检测技术的基本概念■11 3)准确度等级:式(14)中,当△取仪表的最大绝对误差值△.时,引用误差常被用 来确定仪表的准确度等级(Accuracy Class)S,即 (1-5) 根据给出的准确度等级S及量程范围,也可以推算出该仪表可能出现的最大绝对误差 △。准确度等级S规定取一系列标准值。我国的工业模拟仪表有下列常用的7种等级: 0.1、0.2、0.5、1.0、1.5、2.5、5.0。消若测量技术的进步.目前部分行业的议表还增加 了以下几种准确度等级:0.005、0.01、0.02、(0.03)、0.05、0.2、(0.25)、(0.3)、(0.35) (0.4)、(2.0)、4.0等。只有在必要时,才可采用括号内的准确度等级。这些准确度等级 分别表示对应仪表的引用误差不应超过的百分比。从仪表面板上的标志可以判断出仪表的等 级。仪表的准确度等级与对应的引用误差如表11所示。一般来说,准确度等级的数值越 小,仪表越昂贵。 表11仪表的常用准确度等级与对应的引用误差 准确度等级 0.1 0.20.5 1.0 1.5 2.5 5.0 对应的引用误差±0.1%±0.2%±0.5%±1.0%±1.5%±2.5% ±5.0% 仪表的准确度在工程中也常称为“精度”(Accuracy),准确度等级习惯上称为精度等 级。根据仪表的准确度等级可以确定测量的最大引用误差和最大绝对误差。例如,在正常情 况下,用0.5级、量程为100℃的温度表来测量温度时,可能产生的最大绝对误差 △=(±0.5/100)×A=±(0.5%×100)℃=±0.5℃ 在测量领域中,还经常使用正确度、精密度、精确度等名词来评价测量结果。这些术语 的叫法虽然十分普遍,但也比较容易引起混乱。本书只采用准确度这个名词来表达测量结果 误差的大小。 在正常工作条件下,仪表的最大绝对误差多数情祝下是不变的,而示值相对误差y随示 值的减小而增大。例如用上述温度表来测量80℃温度时,相对误差Y,=(±0.5℃/80℃)× 100%=±0.525%,而用它来测量10℃温度时,相对误差Y.=(±0.5℃/10℃)×100%=±5%。 例1-1某压力表准确度为2.5级,量程为0~1.5MPa,求: 1)可能出现的最大满度相对误差Y 2)可能出现的最大绝对误差△.为多少千帕? 3)测量结果显示为0.70NPa时,可能出现的最大示值相对误差Y,。 解1)可能出现的最大满度相对误差可以直接查表1-1得到,即ym=±2.5%。 2)△=yA.=±2.5%×l.5MPa=±0.0375MPa=±37.5kPa 3)%×100%=85x10隆=536%。 由上例可知,y,的绝对值总是大于(在满度时等于)Y。 例1-2现有准确度为0.5级的0-300℃和准确度为1.0级的0~100℃的两个温度计 要测量80℃的温度,试问采用哪一个温度计好? 解经计算,用0.5级表以及1.0级表测量时,可能出现的最大示值相对误差分别为 ±1.88%和±1.25%。计算结果表明,用1.0级表比用0.5级表的示值相对误差的绝对值反

12■自动检测技术及应用第3版 而小,所以更合适。 由上例可知,在选用仪表时应兼顾准确度等级和量程,通常希望示值落在仪表满度值的 2/3左右。 2.测量误差的分类 误差产生的原因和类型很多,其表现形式也多种多样,针对造成误差的不同原因有不同 的解决办法。 按误差性质分类,测量误差有: (1)粗大误差超出在规定条件下预计的误差或明显偏离真值的误差称为粗大误差 (Gross Error),也称疏忽误差,或粗差。粗大误差主要是由于测量人员的粗心大意及电子测 量仪器受到突然而强大的干扰所引起的。如测错、读错、记错、外界过电压尖峰干扰等造成 的误差。就数值大小而言,粗大误差明显超过正常条件下的误差。当发现粗大误差时,应予 以剔除。 (2)系统误差在重复性条件下,对同一被测量进行无限多次重复测量所得结果的平 均值与被测量的真值之差,称为系统误差(Systematic Error),即 系统误差=无限次测量的平均值一真值 有时也采用如下的表达:误差的数值固定或按一定规律变化者,属于系统误差。按其表 现的特点,可分为恒值误差和变值误差两大类。恒值误差在整个测量过程中,其数值和符号 都保持不变。例如,由于刻度盘分度差错或刻度盘移动而使仪表刻度产生的误差,皆属 此类 引起系统误差的因素为系统效应。例如,环境温度及湿度波动、电源电压下降、电子元 件老化、机械零件变形移位、仪表零点漂移等。又如,用零点未调整好的天平称量物体,称 量结果会产生偏高或偏低。 系统误差具有规律性,因此可以通过实验的方法或引人修正值的方法计算修正,也可以 重新调整测量仪表的有关部件使系统误差尽量减小。 由于系统误差及产生的原因不能完全知晓,因此通过修正和调整只能有限程度地对系统 误差进行补偿,其系统误差会比修正前的要小,但不可能为零。 (3)随机误差 测量结果与在重复条件下对同一被测量进行无限多次测量所得结果的 平均值之差称为随机误差(Random Error)。由于实际上只能进行有限次测量,因而只能得 出这一测量结果中随机误差的估计值。随机误差大多是由影响量的随机变化引起的,这种变 化带来的影响称为随机效应,它导致重复观测中的分散性。测量列中的每一个测量结果的随 机误差是不相同的。随着重复次数的增加,出现的随机误差的总和趋向于零,即随机误差可 以认为是测量误差中期望为零的误差分量。 随机误差有时也采用如下的表达:在同一条件下,多次测量同一被测量,有时会发现测 量值时大时小,误差的绝对值及正负以不可预见的方式变化,该误差称为随机误差。随机误 差反映了测量值离散性的大小。引起随机误差的因素称为随机效应。随机误差是测量过程中 许多独立的、微小的、偶然的因素引起的综合结果。 在有随机误差的测量结果中,虽然单个测量值误差的出现是随机的,既不能用实验的方 法消除,也不能修正,但是就误差的整体而言,服从一定的统计规律。因此可以通过增加测 量次数.用概率论的一些理论和统计学的一些方法,堂据看似毫无规律的随机误差的分布

第1章检测技术的基本概念圆13 特性,并进行测量结果的数据统计处理。多数随机误差都服从正态分布规律,我们将在以下 的内容中加以论述。 (4)静态误差和动态误差从测量的静态特性和动态特性来分类,还可将误差分为静 态误差和动态误差。 I)静态误差:在被测量不随时间变化时所产生的误差称为静态误差(Static Error,也 称静态偏差)。前面讨论的误差多属于静态误差。 2)动态误差:当被测量随时间迅速变化时,系统的输出量在时间上不能与被测量的变 化精确吻合,这种误差称为动态误差(Dynamie Error,也称动态偏差)。例如,被测水温以 很快的速度上升到100℃,玻璃水银温度计(属于一阶系统)的水银柱不可能立即上升到 100℃。如果此时就记录读数,必然产生误差。 引起动态误差的原因很多。例如,用笔式记录仪(属于二阶系统)记录心电图时,由 于记录笔的惯性较大,所以记录的结果在时间上滞后于心电的变化,有可能记录不到特别尖 锐的窄脉冲,而且还存较长的稳定时间。不同动态响应的心电图仪测量同一个人的心电图时 的曲线如图13所示。由于其中一台放大器的带宽不够,动态误差较大,描绘出的窄脉冲幅 度偏小。又如,用放大器放大含有大量高次谐波的周期信号(例如很窄的矩形波)时,由 于放大器的频响及电压上升率不够,电路中的积分常数较大,造成高频段的放大倍数小于低 频段,在示波器上看到的波形失真很大,属于系统误差。 a) h 图13不同动态响应的心电图仪测量同一个人的心电图时的曲线 )动态误差较小的心电图仪测量结果b)动态误差较大的心电图仪测量结累 图1-4为一个突变的被测量引起某个二阶系统的瞬态响应曲线。在,时刻,被测量x突 然从零阶跃到1.0y.,但由于测量仪表的输出无法立即跟上输入的变化,得到图14b所示的 响应曲线。图中所示的主要性能指标有:延迟时间4、上升时间(,、峰值响应时间,、调整 时间,、超调量M,等,仪表的输出最终稳定在静态误差允许的范围内。同理,在2时刻, 被测量的突然减小,也存在较长的稳定过程。 一般静态测量要求仪器的带宽在0~10Hz左右,而动态测量要求带宽上限较高(例如 要求大于1OkHz)。这就要求采用高速运算放大器,并尽量减小电路的时间常数。 对用于动态测量、带有机械结构的仪表而言,应尽量减小机械惯性,提高机械结构的谐 振频率,才能尽可能真实地反映被测量的迅速变化
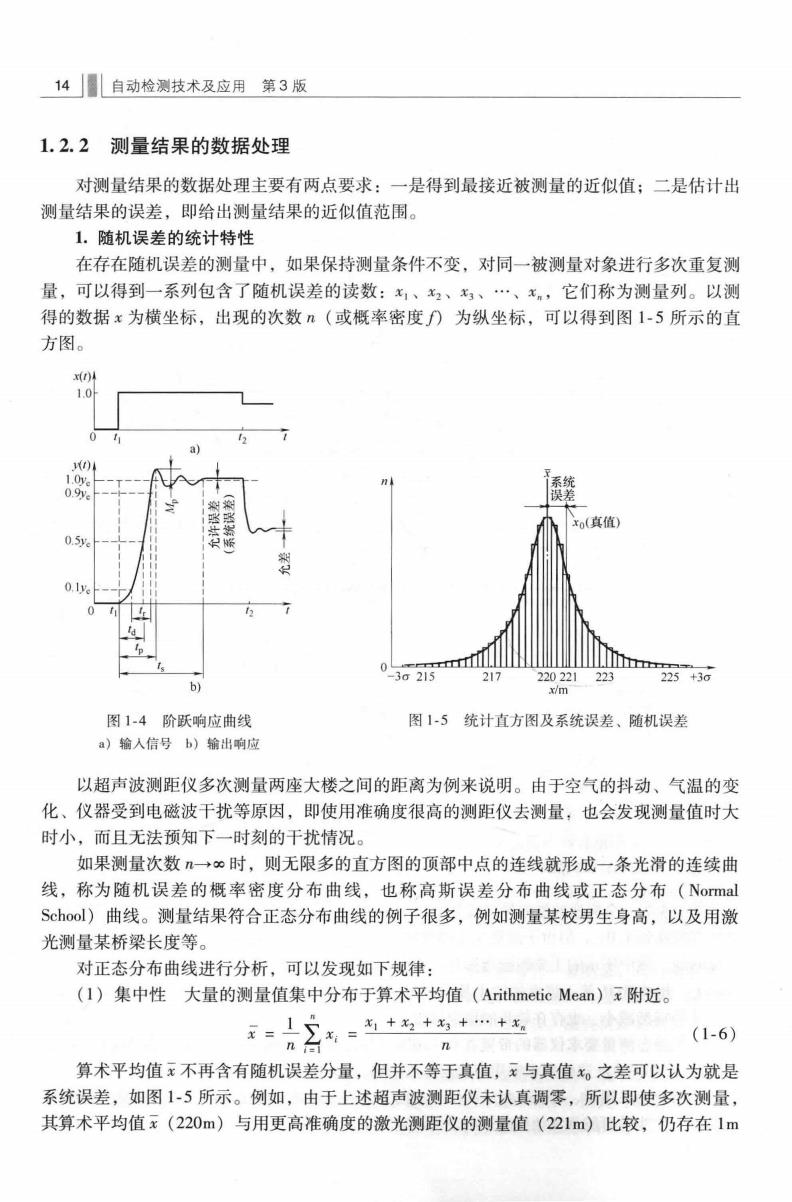
14自动检测技术及应用第3版 1.2.2测量结果的数据处理 对测量结果的数据处理主要有两点要求:一是得到最接近被测量的近似值;二是估计出 测量结果的误差,即给出测量结果的近似值范围。 1.随机误差的统计特性 在存在随机误差的测量中,如果保持测量条件不变,对同一被测量对象进行多次重复测 量,可以得到一系列包含了随机误差的读数:名、名2、名、…、x,它们称为测量列。以测 得的数据x为横坐标,出现的次数(或概率密度)为纵坐标,可以得到图1-5所示的直 方图。 a) 系统 x(直值】 0.5y b) 图14阶跃响应曲线 图15统计直方图及系统误差、随机误差 a)输人信号b)输出响应 以超声波测距仪多次测量两座大楼之间的距离为例来说明。由于空气的抖动、气温的变 化、仪器受到电磁波干扰等原因,即使用准确度很高的测距仪去测量,也会发现测量值时大 时小,而且无法预知下一时刻的干扰情况。 如果测量次数一时,则无限多的直方图的顶部中点的连线就形成一条光滑的连续曲 线,称为随机误差的概率密度分布曲线,也称高斯误差分布曲线或正态分布(Normal Sh)曲线。测量结果符合正态分布曲线的例子很多,例如测量某校男生身高,以及用激 光测量某桥梁长度等。 对正态分布曲线进行分析,可以发现如下规律: (I)集中性大量的测量值集中分布于算术平均值(Arithmetic Mean)x附近。 (1-6) 算术平均值x不再含有随机误差分量,但并不等于真值,x与真值x。之差可以认为就是 系统误差,如图15所示。例如,由于上述超声波测距仪未认真调零,所以即使多次测量 其算术平均值元(220m)与用更高准确度的激光测距仪的测量值(221m)比较,仍存在1m