第五章电路频率响应和谐振现象 目录 5.1频率响应与网络函数 一、网络函数 *二、波特图的概念 5.2一阶电路和二阶电路的频率响应 一、一阶电路 西安电子科技大学电路与系统多媒体室制作 *二、二阶电路 5.3串联谐振电路 一、电路谐振的概念 二、串联谐振 三、串联谐振的属性参数 四、品质因数的物理意义 五、串联谐振的特点 六、频率响应 5.4并联谐振电路 一、GCL并联电路 二、实用简单并联谐振电路 三、复杂并联谐振电路 第5-1页前一页下一页退出本章 点击目录,进入相关章节
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 5.1 频率响应与网络函数 一、网络函数 *二、波特图的概念 5.2 一阶电路和二阶电路的频率响应 一、一阶电路 *二、二阶电路 5.3 串联谐振电路 一、电路谐振的概念 二、串联谐振 三、串联谐振的属性参数 四、品质因数的物理意义 五、串联谐振的特点 六、频率响应 5.4 并联谐振电路 一、GCL并联电路 二、实用简单并联谐振电路 三、复杂并联谐振电路 点击目录 ,进入相关章节 第 5-1 页 前一页 下一页 退出本章 目录
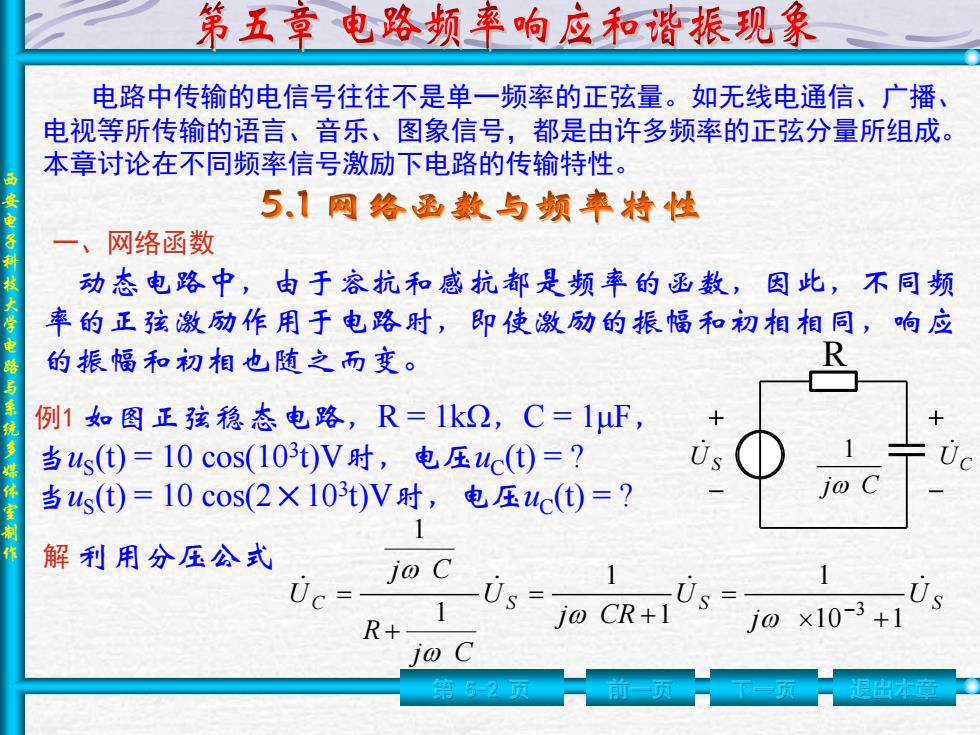
第五章电路频率响应和谐振现象 电路中传输的电信号往往不是单一频率的正弦量。如无线电通信、广播、 电视等所传输的语言、音乐、图象信号,都是由许多频率的正弦分量所组成。 本章讨论在不同频率信号激励下电路的传输特性。 5.1网络西数与频率特性 一、网络函数 动态电路中,由于容抗和感抗都是频率的函数,因此,不同频 率的正弦激励作用于电路时,即使激励的振幅和初相相同,响应 的振幅和初相也随之而变。 例1如图正孩稳态电路,R=1k2,C=1F, 当us(t)=10cos(103t)V时,电压uC(t)=? Us 当4s()=10cos(2×103t)V时,电压c(①)=? j@ 解利用分压公式 jo C Uc- Us= Us 0CR+0s0x103+ R+ jo C
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-2 页 前一页 下一页 退出本章 电路中传输的电信号往往不是单一频率的正弦量。如无线电通信、广播、 电视等所传输的语言、音乐、图象信号,都是由许多频率的正弦分量所组成。 本章讨论在不同频率信号激励下电路的传输特性。 动态电路中,由于容抗和感抗都是频率的函数,因此,不同频 率的正弦激励作用于电路时,即使激励的振幅和初相相同,响应 的振幅和初相也随之而变。 例1 如图正弦稳态电路,R = 1kΩ,C = 1μF, 当uS (t) = 10 cos(103 t)V时,电压uC (t) = ? 当uS (t) = 10 cos(2×103 t)V时,电压uC (t) = ? U S UC R j C 1 解 利用分压公式 C S S U S j U j CR U j C R j C U 10 1 1 1 1 1 1 3 一、网络函数

第五章电路频率响应和振现象 当s()=10cos(10t)V时, 0=10209p,0=103ad/s,0=0.-707∠-45v 1+1 c()=7.07cos(103t-45°)V 当s()=10cos(2×10t)V时, 0m=10☑0Ψ,0=2×103rad1s,Uom= i,=447-63.4V 2+1 c(①)=4.47cos(2X103t-63.4°)V 这种电路的响应随激励频率而变化的特性称为电路的频率特性。 通常用正孩稳态电路的网络函数Network function)描述
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-3 页 前一页 下一页 退出本章 当uS (t) = 10 cos(103 t)V时, 7.07 45 V 1 1 1 10 0 , 10 / , 3 Sm Cm USm j U V rad s U uC (t) = 7.07 cos(103 t- 45°)V 当uS (t) = 10 cos(2× 103 t)V时, 4.47 63.4 V 2 1 1 10 0 , 2 10 / , 3 Sm Cm US j U V rad s U uC (t) = 4.47 cos(2×103 t – 63.4 °)V 这种电路的响应随激励频率而变化的特性称为电路的频率特性。 通常用正弦稳态电路的网络函数(Network function)描述

第五章电路频率响应扣谐派现象 网络函数的定义: f响应相量Y H(jo)= 单激励源作用下 激励相量 如前例, H(jo) Uc. Us j@CR+1 网络函数一般是。的复函数,可写为 H(jo)=H(jo)e 其中,HGjo)川称为电路的幅频特性(amplitude response), 0(o)称为相频特性(phase response), 合称电路的频率特性(频率响应)
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-4 页 前一页 下一页 退出本章 网络函数的定义: F ( ) def 激励相量 响应相量Y H j 如前例, U S UC R j C 1 1 1 ( ) U j CR U H j S C 网络函数一般是ω的复函数,可写为 ( ) ( ) ( ) e j H j H j 其中,|H(jω)|称为电路的幅频特性(amplitude response), θ(ω)称为相频特性(phase response), 合称电路的频率特性(频率响应)。 单激励源作用下

第五章电路频率响应和脂振现象 对前例,Hjo= H(j) +l@CRP 0.707 0(@)=-arctan(@CR) 0 Wc 可见,该电路对低频信号有较大输出,而 对高频分量有抑制作用,故称该电路为低 (a) 通电路,相应网络函数称低通函数。 日(w) 通常将H(Go)/Hmax>0.707的频率范围 0 称为该电路的通带; Wc 而将H(Go)/Hmax<0.707的频率范围称为 -45p 止带或阻带; -90 二者的边界角频率0称为截止角频率。 (b) 当0=Oc时,电路的输出功率是最大功率 的一半,故Qc也称半功率点频率
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-5 页 前一页 下一页 退出本章 2 1 1 ( ) CR H j () arctan( CR) 1 0.707 0 ω C ω (a) |H(jω)| 0 ω -45° -90° θ(ω) (b) ω C 可见,该电路对低频信号有较大输出,而 对高频分量有抑制作用,故称该电路为低 通电路,相应网络函数称低通函数。 对前例, 通常将|H(jω)|/Hmax > 0.707的频率范围 称为该电路的通带; 而将|H(jω)|/Hmax < 0.707的频率范围称为 止带或阻带; 二者的边界角频率ωC称为截止角频率。 当ω= ωC时,电路的输出功率是最大功率 的一半,故ωC也称半功率点频率