
2.5阅读材料:解析函数的保角性 25 2.5阅读材料:解析函数的保角性 函数的解析性是讨论复变函数的微积分的最基本要求.这一看似简单的要求, 实际上对函数施加了很强的限制.这从柯西黎曼方程已经可以看出一些端倪。从 函数的解析性出发,可以导出函数的许多重要特性.复变函数理论的主要研究对 象,就是解析函数.以后各章将逐步介绍解析函数的方方面面。这一节,先侧重于 从几何的角度简要讨论解析函数的应用. 复变函数代表了一个变换,或称映射.在变换(=(z)之下,z平面上的 点变换为(平面上的相应一点.如果函数(=(z)是连续的,z点邻域内的一点 当然也应该变为相应的(点的邻域内的一点.但是,z平面上的一个区域,是否也 变换为(平面上的一个区域,区域的边界是否仍变换为区域的边界,并不是任何 复变函数都能够保证做到的.例如,函数(=Rz就把整个z平面变换为S平面 上的实轴,后者甚至不构成一个区域.可以证明:解析函数可以保证z平面上的 一个区域仍变换为(平面上的一个区域,区域的边界仍变换为区域的边界,边界 的方向也保持不变。换句话说,边界的内部区域仍然变换为相应边界的内部区域 当然,解析函数(2)=常数除外. 设(-f(z)在区域G内解析,0为G内一点.(=f()代表了一个变换(映 射).它把z平面上的区域G映射为(平面上的区域G,把0点映射为相应的 Go=fz0)点.在2.1节中曾经提到,当f(0)≠0时,f'(0川是把0处的微元 dz映射为o处的微元d(的伸缩率(放大倍数),而argf'(2o)(这里不妨限制在主 值范围内),则给出映射的偏转角,即d(与z的辐角差.可以设想,如果在z平 面上有两条曲线1和2相交于0,那么,在(平面上,必然也有相应的两条曲线 5和5相交于0点.由于 (co)=in a)/(o) 2-20 的数值,包括1f'(20)川和argf'(zo),和z趋于o的方式无关,因此,和1与2相 比,片与5应该偏转了同样大小的角度.这就是说,在解析函数所代表的变换之 下,两条曲线之间的夹角保持不变(见图2.9).正是因为这个原因,解析函数所代 表的变换(映射)就称为保角变换(保角映射).当然,在不同点处,即使'()均不 x平面 5西 2 z-5=网 图2.9解析函数所代表的变换的保角性

26 第二章解析函数 为0,变换都具有保角性,但由于数值不同,因而各处的伸缩率和偏转角均不同 所以,区域的几何形状就会发生变化.我们正是要选择合适的保角变换,把z平 面上形状比较复杂的区域变换为(平面上形状比较简单的区域.例如,把之平面 上两个不相交的圆周所围成的区域变换为(平面上同心圆周所围成的区域。 解析函数所代表的变换的保角性,是有条件的:只在'()≠0处才一定有保 角性.在f'(z)=0的点,由于argf'(z)没有确定值,因而变换可能是保角的,也 可能是不保角的.巧妙地利用变换在'()=0处的不保角性,更可以把(z平面 口拾遗补 、上的)复杂图形变换为(《平面上的)简单图形.例如,可以把多边形变为圆周. 将保角变换应用于解决实际问题,不仅涉及区域形状的变化,还涉及数学表 述形式(例如微分方程)的变化.可以想象,只有在区域的形状变得更简单,同时 又不增加微分方程的复杂性的条件下,保角变换才具有实用价值 就本课程而言,我们特别有兴趣于讨论二维拉普拉斯算符 02 v2=ap2+册 (2.17) 在解析函数(=+i切=(z)所代表的变换(红,)→(传,)下的变化.根据偏微商的 链式法则, 品+品 8 86 8 8n 8 成=所展+列所 品-器是+品+()器+()'器+器院 所以 =+ -()+()月+()°+()器 +(器+)吴+(+)品+(驶+》 再利用练习2.3中的结果及(2.4)和(2.5)式,就能得到 -rer(g+那) (2.18) 此结果表明:在解析函数(=(z)所代表的保角变换之下,二维拉普拉斯方程 (am+au(,)=0, (2.19)

习题 27 在'(2)≠0的点,仍保持为二维拉普拉斯方程 (g+)eee-g (2.20) 二维泊松方程 /a22 (证+)u,)=pe, (2.21) 在变化后也仍然是二维泊松方程 (震+)-e-高 82 (2.22) 练习2.13证明:在解析函数(=5+切=f()所代表的保角变换下,面积元的变化公 式是 drdy=()2dedn. 因此,如果把泊松方程设想为平面静电场的方程,非齐次项是面电荷密度,则电荷守恒 p(z,y)drdy=o(,n)dEdn. 在解析函数(=f()所代表的保角变换之下,二维亥姆霍兹方程 (器+器)e+=0 92 (2.23) 在'(2)≠0的点,也保持为二维亥姆霍兹方程 (宽+器)4e训+re账训=0 k2 (2.24) 这样,应用保角变换,就可以把形状比较复杂的区域内的拉普拉斯方程、泊松 方程或亥姆霍兹方程的求解问题,转换为形状比较简单的区域(例如,圆)内的求 解问题. 习题 1.判断下列函数在何处可导(并求出其导数),在何处解析: 囚习题答案 (): (2)2; (3)zRez; (④)(x2+2)+i(x2+y2) (⑤)3x2+2iy3 (6)(x-)2+2i(x+y). 2.证明平面极坐标系(,)下的柯西黎曼方程: 架-阳杂瑞 u(r,)和v(r,)分别为复变函数的实部和虚部

28 第二章解析函数 3.利用平面极坐标系(r,)下的柯西黎曼方程证明: r-(=+器)(阳-) 4.设z=x+ig,已知解析函数f(z)=u(红,)+iu(红,)的实部u(红,)如下, 试求出解析函数f(z): 1)x2-y2+; (②2+y (3)ev cosz; (4)cosx coshy. 5.设z=x+划,已知解析函数f(z)=u(x,)+iw(x,)的实部或虚部如下, 试求f(z): (1)u=x+5 (2)u=sin coshy 6.若f()=u(c,)+iu(c,)解析,且u-v=(红-(x2+4xy+2),试求 f(z). 7解下列方程: 0血:-+ (2)cosz=4; (3)tanz=i; (4)2cosh2z-3cosh z+1=0. 8.判断下列函数是单值的还是多值的: (1)V2-1 (2)2+√2-1 (3)sin (4)cosv; 典是 (6)cos (7)Insinz; (8)sin (iInz). 9.找出下列多值函数的枝点,并讨论z绕一个枝点移动一周回到原处后函数 值的变化.如果同时绕两个乃至更多个枝点一周,函数值又如何变化? (1)V2-a(2-b,a≠b (2)/2-a(z-可,a≠b: 阅V活斯 0品收 (5)V1-z; (6)1-z: ()(22+1片 (8)In cosz. 10.求下列函数在指定点的全部可能取值: (1)n2,2=1,i,-1,1+i (2)2,z=2,i,-1,(1+i0
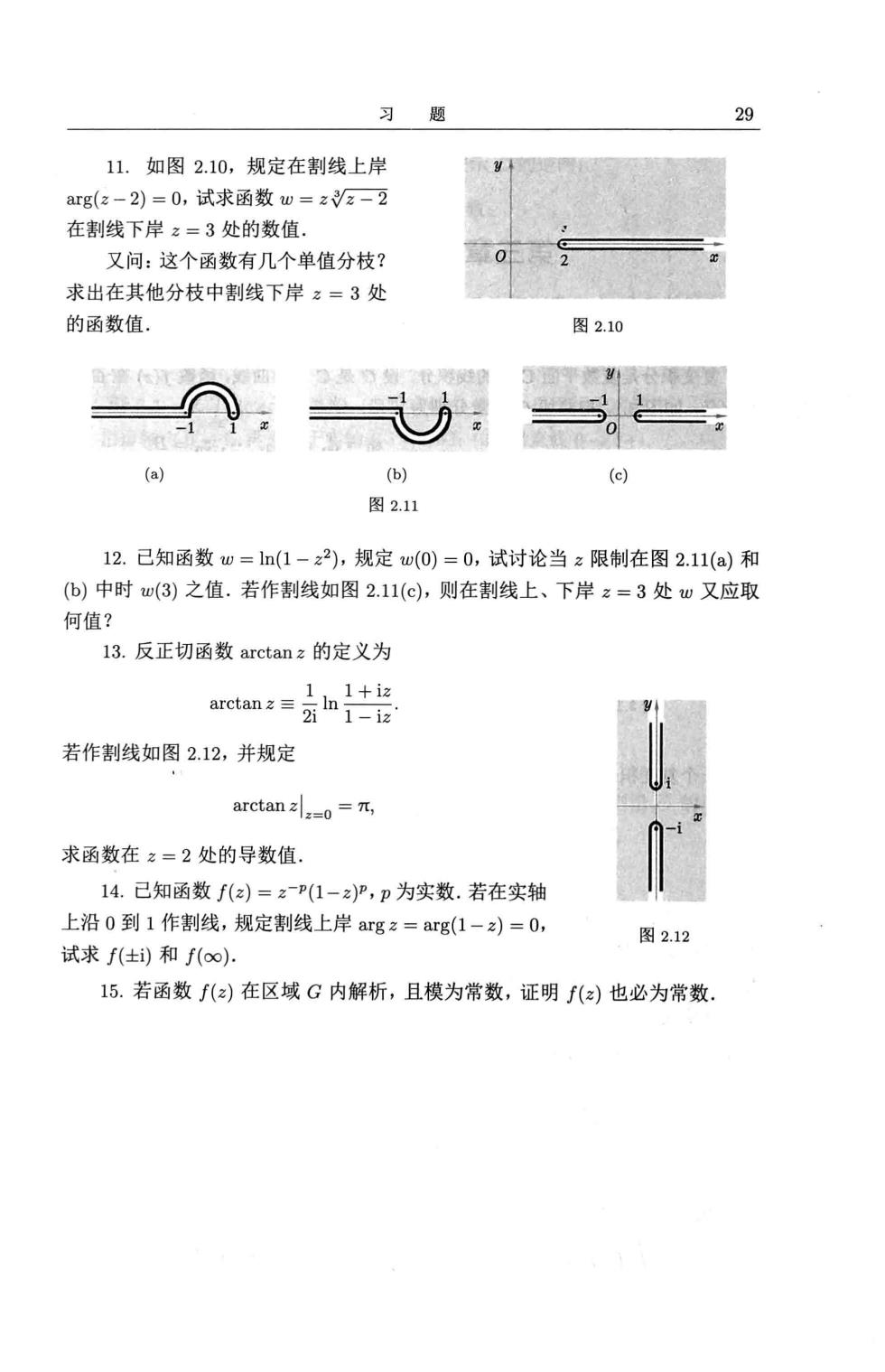
习题 29 11.如图2.10,规定在割线上岸 arg(z-2)=0,试求函数w=zz-2 在割线下岸z=3处的数值。 又问:这个函数有几个单值分枝? 0 求出在其他分枝中割线下岸z=3处 的函数值 图2.10 图2.11 12.已知函数w=ln(1-z2),规定w(0)=0,试讨论当z限制在图2.11(a)和 (b)中时w(3)之值.若作割线如图2.11(c),则在割线上、下岸z=3处w又应取 何值? l3.反正切函数arctanz的定义为 若作割线如图2.12,并规定 arctan=0=元 求函数在z=2处的导数值. 14.已知函数f(2)=2P(1-z)P,p为实数.若在实轴 上沿0到1作割线,规定割线上岸argz=arg(1-2)=0, 图2.12 试求f(±i)和f(o∞). 15.若函数f(z)在区域G内解析,且模为常数,证明f()也必为常数