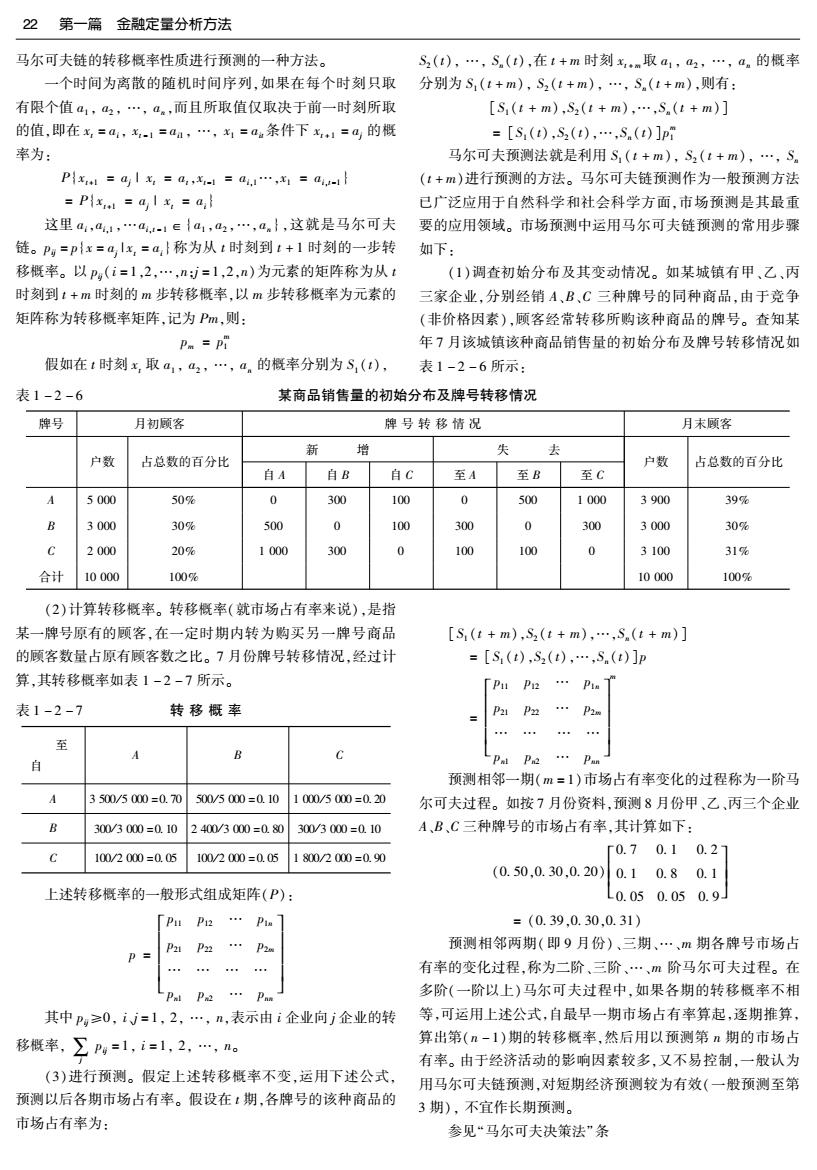
22第一篇金融定量分析方法 马尔可夫链的转移概率性质进行预测的一种方法。 S2(t),…,S(t),在t+m时刻xm取a1,a2,…,a。的概率 一个时间为离散的随机时间序列,如果在每个时刻只取 分别为S,(t+m),S2(t+m),…,S(t+m),则有: 有限个值a1,2,…,4。,而且所取值仅取决于前一时刻所取 [S(t+m),S2(t+m),…,Sn(t+m)] 的值,即在x,=a,x,.1=aa,…,x1=aa条件下x1=a的概 =[S(t),S2(t),…,Sn(t)]p 率为: 马尔可夫预测法就是利用S,(t+m),S2(t+m),…,S。 Pxl=a|x=a,x-1=a4,1…,x1=a4-} (:+m)进行预测的方法。马尔可夫链预测作为一般预测方法 =Plx=al x,=a 已广泛应用于自然科学和社会科学方面,市场预测是其最重 这里a4,a,1,…a,-1e{a1,2,…,a.},这就是马尔可夫 要的应用领域。市场预测中运用马尔可夫链预测的常用步骤 链。Pg=p{x=alx,=a,}称为从t时刻到t+1时刻的一步转 如下: 移概率。以Pg(i=1,2,…,n=1,2,n)为元素的矩阵称为从t (1)调查初始分布及其变动情况。如某城镇有甲、乙、丙 时刻到t+m时刻的m步转移概率,以m步转移概率为元素的 三家企业,分别经销A、B、C三种牌号的同种商品,由于竞争 矩阵称为转移概率矩阵,记为Pm,则: (非价格因素),顾客经常转移所购该种商品的牌号。查知某 P Pi 年7月该城镇该种商品销售量的初始分布及牌号转移情况如 假如在t时刻x取a1,a2,…,an的概率分别为S(t), 表1-2-6所示: 表1-2-6 某商品销售量的初始分布及牌号转移情况 牌号 月初顾客 牌号转移情况 月末顾客 新 增 失 去 户数 占总数的百分比 户数 占总数的百分比 自A 自B 自C 至A 至B 至C 5000 50% 0 300 100 0 500 1000 3900 39% B 3000 30% 500 0 100 300 0 300 3000 30% 2000 20% 1000 300 0 100 100 0 3100 31% 合计 10000 100呢 10000 100% (2)计算转移概率。转移概率(就市场占有率来说),是指 某一牌号原有的顾客,在一定时期内转为购买另一牌号商品 [S(t+m),S2(t+m),…,Sn(t+m)] 的顾客数量占原有顾客数之比。7月份牌号转移情况,经过计 =[S(t),S2(t),…,S.(t)]p 算,其转移概率如表1-2-7所示。 P P12 Pin 表1-2-7 转移概率 P21 至 预测相邻一期(m=1)市场占有率变化的过程称为一阶马 3500/5000=0.70 500/5000=0.10 1000/5000=0.20 尔可夫过程。如按7月份资料,预测8月份甲、乙,丙三个企业 300/3000=0.10 2400/3000=0.80 300/3000=0.10 A,B、C三种牌号的市场占有率,其计算如下: 0.1 0.21 100/2000=0.05 100/2000=0.05 1800/2000=0.90 r0.7 (0.50,0.30,0.20) 0.10.80.1 上述转移概率的一般形式组成矩阵(P): L0.050.050.9 Pu P12 =(0.39,0.30,0.31) P22 预测相邻两期(即9月份)、三期、…、m期各牌号市场占 有率的变化过程,称为二阶、三阶、…、m阶马尔可夫过程。在 PP 多阶(一阶以上)马尔可夫过程中,如果各期的转移概率不相 其中Pg≥0,iJ=1,2,…,n,表示由i企业向j企业的转 等,可运用上述公式,自最早一期市场占有率算起,逐期推算, 移概率,∑Pg=1,i=1,2,…,n。 算出第(n-1)期的转移概率,然后用以预测第n期的市场占 有率。由于经济活动的影响因素较多,又不易控制,一般认为 (3)进行预测。假定上述转移概率不变,运用下述公式, 用马尔可夫链预测,对短期经济预测较为有效(一般预测至第 预测以后各期市场占有率。假设在:期,各牌号的该种商品的 3期),不宜作长期预测。 市场占有率为: 参见“马尔可夫决策法”条

第2章金融预测分析方法23 时间序列预测法(Time-series Methods of Forecas-t,对数线性模型y,=a+b1l,幂函数曲线模型y,=ae“,指数曲 ting) 线模型y,=ab或y,=ae7,二次曲线模y,=b+bt+bt2,三次曲 时间序列预测法又称外推法或历史延伸法,是指将客观 线模型y,=b+bt+b2+br,修正指数曲线模型y,=L+ae“,龚 事物随时间变化所形成的规律用数学模型描述,并用此模型 珀兹曲线模型y,=ee-或y=a“,皮尔曲线模型y=L+ae 推断其未来状况的预测方法。它把同一经济变量的实际数据 等。一般的趋势模型可以通过一定的变换手段将其线性化, 按时间顺序排列,应用数学方法进行分析,找出其中的变化趋 然后采用最小二乘法以估计其参数。如指数曲线模型两边同 势和规律性。时间序列简称时序,是指按时间间隔先后排列的 时取对数后变为:lgy=lga+lgb1,以时间顺序号t为自变量, 数据序列。在不同的时刻观测同一经济变量得到的数据,往往 lgy为因变量,采用最小二乘法估计其参数即可得到lga与lgb 存在着差异,这是因为时间序列经常受到一种或数种变动因素 的数值,求lga的反对数即可得到a的值。有增长上限的一类 作用的结果。这些变动因素可以归纳为长期变动趋势、季节性 趋势模型,当极限值L可以事先确定时(凭经验或估计)也容 变动、周期性变动、不规则变动。时间序列分析预测技术可以分 易线性化,并用最小二乘法以估计另外两个参数A、B:若极限 为确定型时间序列分析和随机型时间序列分析。目前,前者应 值无法事先确定,可以采用三和值法对参数进行粗略的估计, 用较多。时间序列分析预测技术的程序有:①数据处理。目的 即将时间序列的样本数据分为三段,每段W期,分别求出这三 是消除季节性变动、周期性变动和不规则变动因素,使其经过 段的和: 处理后仅包括长期变动趋势的数据。②建立数学模型。根据 数据处理以后得到的长期趋势,建立时间序列的预测模型。③ ∑,∑2,∑3y 修正预测模型。主要是用季节性变动和周期性变动及预测结 然后用这三个值求解三个参数L、a、b。如修正指数曲线 果对模型进行修正。④进行预测。确定型时间序列分析技术 可求得: 不涉及时间序列的随机特性及实质。根据不同变动因素作用 b=[(∑3y,-∑2,)/∑2y,-∑1y,](1/m) 的大小,其方法也不相同。当其他几种变动因素较弱,长期变动 a=(∑2y,-∑1y,)(e-1)/(e-1) 趋势明显时,可以采取直接建立预测模型的方法。当几种变动 L={[∑y,-∑3y-(∑2y,)]V 因素同时作用而使时间序列的长期趋势不明显时,则要先进行 数据处理,消除不规则变动、周期变动和季节变动因素的影响, [1y,+∑3y-1∑x,]Yn 然后建立预测模型,还可以直接利用时间序列的平均值进行预 龚珀兹曲线和皮尔曲线都可设法变换为修正指数曲线的 测。时间序列预测法所需要的只是预测对象本身的历史数据, 形式,利用三和值法计算参数。具有某种上升或下降趋势的 因而运用较为方便,其预测是否有效的关键在于模型的选择。 时间序列可以从绘制的时间序列曲线图上直观地识别选用何 随机型时间序列分析预测技术以时间序列的随机性为研究对 种模型。选择的趋势模型是否适用于预测,需进行模型分析 象,并用数学模型来进行描述。随机型时间序列分析是随着计 若模型精度较高,且对未来趋势的表现能力较强,可以被接受 算机的应用而发展起来的。在一般的预测决策及管理工作中 用于预测。若初选了几个模型,则要通过分析选择误差小的 涉及到的时间序列,大多数是由随机过程产生的。描述随机过 并能较好表现时间序列未来变化的模型。 程的主要特征是平均值、方差、均方差和相关系数。随机过程可 2.移动平均法 分为平稳过程和非平稳过程。对于平稳过程建立随机型时间 移动平均法是在简单平均法基础上发展起来的。它是将 序列的线性模型较为容易。在实际预测中所涉及的时间序列 期的时间序列数据加以平均,用平均值作为预测值的方法。 大多数是由低阶的齐次非平稳过程产生的。而这种过程经数 其预测模型可写成下式: 学处理较容易化为平稳过程。因此,在实际预测中应用随机型 Mx1=y=(1+y2+…+yn)/N 的线性模型是现实的。随机型时间序列的数学模型主要有:① Mn2=y=(2+为+…+yN1)/N 线性平稳模型[包括滑动平均模型(Moving Average Model),简式中,y(t=l,2,…,N,N+1)是第t期时间序列的实际值, 称MA(n)模型,n为其阶数;②自回归模型(Auto-Regression M,(t=N+1,N+2)是第t期的预测值,N是移动步长,它的作 Modl),简称AR(m)模型,m为其阶数;③自回归移动平均模型 用在于平滑数据,N越大,按平均后的数据绘制成的时间序列 Auto-Regression Integrated Moving Average Model),ARMA 曲线就越平滑。当时间序列数据变化比较平稳时,宜选用较 (m,n)模型,m,n为其阶数:④线性非平稳模型(包括积分滑动 大的N值,如用5期或7期进行平均:而当时间序列数据变化 平均模型、积分自回归模型,积分自回归滑动平均模型):⑤季 波动较大时,应选用较小的N值,如N=3。移动平均法适用 节模型。时间序列预测法主要有以下几种: 于没有明显趋势的时间序列,它只能预测下一期的数值,实用 1.趋势外推法。 性较差。 亦称外推法。它是将时间序列的某种趋势用相应的趋势 3.指数平滑法。参见“指数平滑法”条。 模型描述,并用此模型进行外推预测的方法。常用的趋势模 4.季节周期变动预测法。适用于具有季节性周期变动的 型有:直线模型y=a+bt,曲线模型y,=a+b/1或1/y,=a+b/ 时间序列。若时间序列呈现某种周期性的变化且周期为一年

24第一篇金融定量分析方法 (周期长度为4),则表明其具有季节性变动趋势。对于具有季 时间序列分解理论模型有以下三种: 节性变化而无明显的长期趋势变动的时间序列可以建立季节 (1)加法型Y,=T,+S,+C,+E 性水平模型y=,其中y为时间序列样本数据的平均值,它 (2)乘法型Y=T·S·C,·E, 可以是全部样本的平均,也可取近几年的平均或前一年的平 (3)混合型Y,=T,·S,+C,+E, 均。是季节指数,也称为季节比,若时间序列是分月的资料, 式中,Y一时间序列的原始数据: 则丘有12个:如为分季资料,则丘有4个。季节指数五表明某 T,一长期趋势变动趋势函数: 月(季)由于季节变化影响而带来的高于平均值或低于平均值 S,一季节性变动趋势函数: 的比率: C,—循环性变动趋势函数: =同月(季)平均值/总平均值 E,一随机性变动趋势函数,E,-N(0,2),即服从 式中,总平均值是全部时间序列数据的月(季)平均值。 均值为零,方差为2的正态分布。 既有线性趋势变动又有季节变动的时间序列,当其波动幅度 时间序列分解预测法的基本预测模型是: 随趋势增加而加大时,可以建立季节性交乘趋势模型y= 数据=模型+误差 (a+bt)f.趋势部分U,=a+bt可以采用最小二乘法估计参数求 =f(趋势变动T,季节变动S,循环变动C)+误差(E) 得。将各期实际值与趋势值相比可求得样本季节指数F,: 分解时间序列的方法很多,各种分解方法的目的都是以 F,=y,/0, 尽可能高的精确度将时间序列分解开。 将各年同月(季)的F,加以平均,即得到理论季节指数 f,即: 平均发展速度预测法(Average Speed of Develop- f=(Fr+Fr+…+Fm-i(r)/m ment Prediction) 其中T是季节周期的长度(12个月或4个季),m是时间 平均发展速度预测法,就是运用历史资料计算出总的发 序列的年数,i=1,2,…,12或i=1,2,3,4。若时间序列既 展速度,然后用查表或开方的方法求出平均发展速度,并以此 有线性趋势变动又有季节变动,且波动幅度并不随趋势增加 作为依据的一种预测的依据。这种方法是我们计划工作中经 而加大,可以建立季节性迭加趋势模型y,=(a+bM)+d,趋势 常采用的传统的预测方法之一。它适于对市场商品供应量、 部分巴,=a+bt可用最小二乘法估计参数得到,将实际值与趋 商品流转额、商业职工人数以及企业的经营成果的中期预测 势值相减可得各期的实际季节增量D: 和长期预测。它是用当期乘以平均发展速度作为下期的预 D,=y,-, 测值。 将各年同月(季)季节增量进行平均,即得到理论季节增 现以某地的呢绒销售量为例(如表1-2-8),计算其平均 量d: 发展速度,并求其下年预测值。 d=(D+Di+…+D-ia)/m 各符号意义同前。 表1-2-8 某地1971~1979年呢绒销售量 年份 销售量(万米) 平均发展速度预测销售量(万米) 历史延伸法(Historical Extend Method) 1971 280 1.088 280 见“时间序列预测法”条。 1972 270 1.088 304 1973 310 1.088 331 趋势外推法(Trend Extrapolation Technique) 1974 260 1.088 361 见“时间序列预测法”条。 1975 320 1.088 392 1976 380 1.088 426 时间序列分解预测法(Time-series Analysis Method 1977 520 1.088 463 1978 530 1.088 505 of Forecasting 1979 550 1.088 550 社会经济统计学认为,在一个较长时间的时间序列中,往 n=9 3420 1.088 3612 往同时存在着受不同因素影响的几种变动,如受某根本性原 因所决定的长期趋势变动,在一年之内受自然因素影响的季 先计算出总发展速度之后,再求其平均发展速度: 节变动,在一定时期内受自然和社会因素影响的周期变动以 平均发展速度=1.9643=108.8% 及受不可预测因素影响的随机变动。一个时间序列总是以上 这一指标反映了某地1971年至1979年呢绒销售量发展 四种变动单独、叠加或组合作用的结果。通过一定的数学方 的总趋势。 法分别测定出这四种变动的影响,将其数据化并研究其发展 然后依次计算历年的预测值: 变化的规律,进而对时间序列的未来作出预测,这就是时间序 1980年预测销售量=550×1.088=598.4(万米) 列的分解预测方法。 1981年预测销售量=598.4×1.088=651.1(万米)

第2章金融预测分析方法25 定点平均法(Fixed-.point Average Method) 定点平均法是按存储或使用数据量多少来进行时间序列 iim 分析的预测方法,这种平均处理方法是在通常的统计平均数 对于平均数公式有如下结论: 公式基础上的改造,其定点含义是指在连续预测中,平均化的 元h<max{元,0≤i≤t+k-1}=n 数据序列的起始点不变。因此,连续预测中所使用的数据量 >min{t,0≤i≤t+k-1} 越来越大。其多步(期)预测公式如下: 例:某公司1985~1994年销售额资料如表1-2-9,试预测 t+-1 1995-2000年销售额。 (①第术平均公式:= (1) 表1-2-9 式中, 1 年份 1985198619871988198919901991 199219931994 无is1 销售 额x 220 250225225230215250 235240235 l≥1 i 0 1 2 3 4 5 6 7 8 9 —一大于零的正整数,表示预测期数或步数。 tk-1 显然表1-2-9中的数据是比较平衡的。根据表1-2-9 (2)几何平均公式:名4=Πx0 (2) 资料知t=9,1≤k≤6。 0 1 对上述两式,若令二十则两式分别变为不加权的定 设 地l-l=10gl-1=0gk=0.3 点平均公式,下面我们做一些补充解释。 0k-2=109+-2=10k=0.2 对于(1)、(2)式,详细表达式可写成: -d=wg-3=064=0.5 (d=3,4,t+k) 6 式中, ∑0+∑g=1 显然 ∑-d+0,2+1=1 现把权值系数列表于表1-2-10: 表1-2-10 预测年份 0 3 4 010011 01211 014 1995K=1 1/16 1/16 1/161/161/161/161/161/160.2 0.3 1996K=2 1/18 1/18 1/18 1/181/181/181/181/18 1/18 0.20.3 1997K=3 1/20 1/20 1/201/201/201/201/201/201/201/200.2 0.3 1998K=4 1/22 1/22 1/22 1/221/22 1/221/221/22 1221/22 1/22 0.2 0.3 1999K=5 1/24 1/241/241/241/241/241/241/241241/241/241/240.20.3 2000K=6 1/26 1/261261/26:1/261/261/261/26 1/261/261/261/261/260.2 0.3 依据公式 “宫++和 得 =824+0.2%+0.30 9 主。 =116+17+71 =234 -名t+ 元g3=233 g4=234 =6Σ5+02+0.3 元g5=元4=234 元g46=元200 =116+48+71 12 =235 +元∑+0.24+0.3 2==∑0+} =89+27+47+70 0 =233 上述预测结果见表1-2-11:
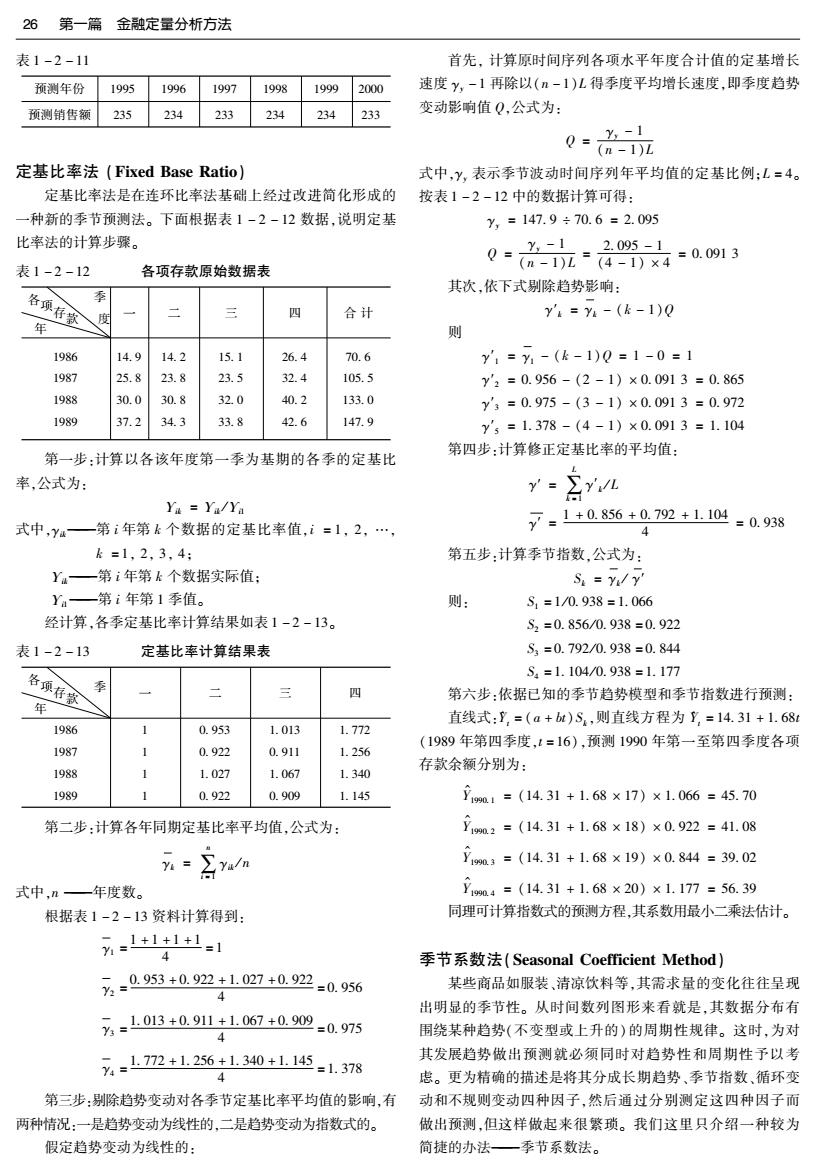
26 第一篇 金融定量分析方法 表1-2-11 首先,计算原时间序列各项水平年度合计值的定基增长 预测年份 1995 1996 1997 1998 1999 2000 速度y,-1再除以(n-1)L得季度平均增长速度,即季度趋势 预测销售额235 234 233 234 234 233 变动影响值Q,公式为: 0品 定基比率法(Fixed Base Ratio) 式中,Y,表示季节波动时间序列年平均值的定基比例;L=4。 定基比率法是在连环比率法基础上经过改进简化形成的 按表1-2-12中的数据计算可得: 一种新的季节预测法。下面根据表1-2-12数据,说明定基 Y,=147.9÷70.6=2.095 比率法的计算步骤。 0=%1 。2.095-1 表1-2-12 各项存款原始数据表 2-1)z4-)×4=0.0913 其次,依下式剔除趋势影响: 各项存登 季 、度 三 四 合计 Y=Y-(k-1)0 年 则 1986 14.9 14.2 15.1 26.4 70.6 y'1=y1-(k-1)0=1-0=1 1987 25.8 23.8 23.5 32.4 105.5 y2=0.956-(2-1)×0.0913=0.865 1988 30.0 30.8 32.0 40.2 133.0 y3=0.975-(3-1)×0.0913=0.972 1989 37.2 34.3 33.8 42.6 147.9 y5=1.378-(4-1)×0.0913=1.104 第一步:计算以各该年度第一季为基期的各季的定基比 第四步:计算修正定基比率的平均值: 率,公式为: r-Ev Y=Ya/Ya 式中,y一第i年第k个数据的定基比率值,i=1,2,…, 7-1+0856+0.792+1104-0.938 4 k=1,2,3,4: 第五步:计算季节指数公式为: Y4—第i年第k个数据实际值: S=yly' Ya—第i年第1季值。 则 S1=1/0.938=1.066 经计算,各季定基比率计算结果如表1-2-13。 S2=0.856/0.938=0.922 表1-2-13 定基比率计算结果表 S3=0.792/0.938=0.844 S4=1.104/0.938=1.177 各项存童 季 三 第六步:依据已知的季节趋势模型和季节指数进行预测: 直线式:,=(a+bt)S,则直线方程为Y,-14.31+1.68 1986 1 0.953 1.013 1.772 (1989年第四季度,1=16),预测1990年第一至第四季度各项 1987 0.922 0.911 1.256 存款余额分别为: 1988 1 1.027 1.067 1.340 1989 0.922 0.909 1.145 立m1=(14.31+1.68×17)×1.066=45.70 第二步:计算各年同期定基比率平均值,公式为: 立m02=(14.31+1.68×18)×0.922=41.08 0,=(14.31+1.68×19)×0.84=39.02 式中,n一年度数。 m04=(14.31+1.68×20)×1.177=56.39 根据表1-2-13资料计算得到: 同理可计算指数式的预测方程,其系数用最小二乘法估计。 =1+1-1 4 季节系数法(Seasonal Coefficient Method) 7-0953+0.92+L.027+0.92=0.956 某些商品如服装、清凉饮料等,其需求量的变化往往呈现 出明显的季节性。从时间数列图形来看就是,其数据分布有 7-1013+091141.067+0909=0.975 4 围绕某种趋势(不变型或上升的)的周期性规律。这时,为对 7-772+125641340+1.145-1.378 其发展趋势做出预测就必须同时对趋势性和周期性予以考 4 虑。更为精确的描述是将其分成长期趋势、季节指数、循环变 第三步:剔除趋势变动对各季节定基比率平均值的影响,有 动和不规则变动四种因子,然后通过分别测定这四种因子而 两种情况:一是趋势变动为线性的,二是趋势变动为指数式的。 做出预测,但这样做起来很繁琐。我们这里只介绍一种较为 假定趋势变动为线性的: 简捷的办法—季节系数法