第2章金融预测分析方法17 与x之间的相关程度如何,也可以说y的值由x变化而决定的 在预测中,运用二元回归预测法就是从3个变量中选择1个变 比重(%)有多大,如果只是从数据散布图来判断是不准确的, 量为因变量,其余2个变量为自变量。二元回归预测法也是 需要应用误差统计原理进行定量的检查,即根据已知数据求 运用最小二乘法来求解待定参数。其思路是:使预测值和实 出一个相关系数(),然后根据r值的大小来判定y与x的相 际数据之间的离差平方总和∑(了-y)尸最小,使回归线最能 关程度,这称之为相关检验。 代表实际变量的变化趋势。 相关系数r计算公式为: 二元回归模型是: n∑(xy)-∑x∑y y=a+bx+b2x2 r= (4) √n∑2-(∑x)2√n∑y-(∑)2 式中,一因变量: r值的大小,反映y与x线性相关的程度,其值的区域为 x一第一个自变量: 2一第二个自变量; -1<r<1。当相关系数r=1或-1时,y与x是密切相关;当 a、b:、b2一待定参数。 相关系数r≈0时,y与x不相关。 式中,a—起点值,是趋势线与y轴的截距: 为了保证回归方程具有最低程度的线性关系,要求,的计 b,一y对x1的回归系数,表明当2固定时,x1平均变 算值大于相应的最低临界值2,这个临界值2就是相关检验 动一个单位时对y的影响程度: 的标准。 b2一y对x2的回归系数,表明当x1固定时,2平均变 由于存在抽样误差,预测值不可能是一个确定值,而应该 动一个单位时对y的影响程度。 是一个范围或区间,一般要求实际值位于这个区间范围的概 关于a、b,b2的求解,根据最小平方法原理,要使Q=(y 率应达到95%以上,这个区间即为预测值的置信区间。置信 -y)2最小须满足: 区间说明回归模型的适用范围或精确程度,当数据点在回归 直线附近大致接近于正态分布时,这个区间应为y±2s,其中s a议-0 da 为标准差。 Q-0 这样可以得出置信区间上、下限的两条控制线,如图 1-2-1所示: a议=0 a 具体计算如下: 1. y=a+bx 梁=品∑(y-a-b4-4尸 =-2∑(y-a-bx1-b) (1) =0 解得:∑y=na+6,∑x+6:∑ 器=武y-a-- =-2x∑(y-a-bx-b2) (2) 图1-2-1 =0 置信区间上限为: 解得:∑y=a∑+6∑好+6:∑ 3 y a bx 2s 置信区间下限为: 器=品∑y-a-66-尸 y2 a bx-2s (3) 其中, =-22∑(y-a-bx1-b42) =0 1-)[∑y-(∑)'/m网 解得:∑y=a∑+b∑+b∑号 n-2 将(1)式、(2)式、(3)式联立 (4) 二元线性回归预测方法(Dual Linear Regression Pre ∑y=na+b,∑x+2∑ (5) diction Method)】 ∑=∑+6,∑+6,∑ 即用2个自变量的变动来推断因变量变化趋势的方法。 ∑y=a∑+b,∑x+b:∑好 (6)

18第一篇金融定量分析方法 将(4)式两边同时除以n,移项有: 种商品的需求量就增加7.19单位。回归模型能否被接受 a y-b x1-b2x2 用于预测也应进行各种检验。首先是回归系数的显著性检 将代入到a=y-b1x1-b2(5)式、(6)式即可求出b:b2。 验,亦即参数的t检验。为此先计算各回归系数b,的t值 tb,根据给定的显著性水平a(通常a=0.05),自由度n- 多元线性回归预测法(Multivariate Linear Regres-(k为参数的个数,如为二元线性回归模型,则待定系数为 sion Prediction Method) 3,而自由度为n-3),查找t分布表,得到临界值t。,若1tb, 多元线性回归预测法主要用于处理多个自变量x, >1,则回归系数显著不为0,表明所选择的自变量是显著 ,…,x。与因变量y之间的关系。它适用于影响预测对象 影响因变量Y的因素:若1b,I<t,则回归系数b与0无显 的因素有多个,且均与预测对象呈线性关系的情况。多元线 著差异,所选自变量不是影响因变量Y的重要因素;如果参 性回归模型的一般形式为: 数:检验均未通过,则回归模型不能被接受用于预测。其次 为回归方程的显著性检验,亦即F检验,它基本上同于一元 y =bo +b+b2x2++bix+e 预测模型为: 线性回归分析法,只是查找F分布表的临界值F。时第一自 y=b。+bx1+b2x2+…+bx 由度为k-1,第二自由度为n-k(k是待定参数的个数)。 式中,b。一是常数项, 第三为参数序列的自相关检验即D.W.检验,也与前面介 b,b2,…,b。—回归系数。 绍相同,只是自变量个数不同,在查找d。及d:时要注意。 在计算模型参数时常写成如下矩阵形式: 第四是拟合优度2检验,由于受到模型中自变量数目多少 Y XB +e 的影响,因而在2检验的同时,还计算R2以消除自变量数 式中,Y一因变量样本数据矩阵: 目带来的影响: X一自变量样本数据矩阵: R2=1-【Σ(Y-P/(n-k))1/ e一误差阵。 【Σ(Y-Y)2/(n-1)] 即 根据R2和R的计算公式,可以推得二者之间的关系: R2=1-(1-R2)(n-1)/(n-k) 当k=1时,R2=R:若k>1,则R2>R2可能为负。一般情况 下如R接近于1,R'也接近于1,则模型的拟合优度为高。第 五是回归标准差的检验,它也同于一元线性回归预测法。在运 用多元线性回归预测法时需注意,自变量之间不能有较强的 相关性,也就是自变量之间不能有共线性。如果两个自变量之 间的相关系数较大,常表明二者有较强的线性关系,如把它们 同时引进回归模型,自变量就会存在共线性。在多元线性回归 模型中,自变量X的数目越多(越大),求解方程式也越困 难。在这种情况下,应该进行降维处理,即将x1,x2,…,x。这口 个变量中关系比较密切的变量化为一类,以减少总变量的个 数,使得模型中只包含所有对Y影响显著的自变量,而不包含 对Y影响不显著的自变量。选择这样的“最优”回归模型的方 法有四种:①穷举法。即从所有可能的自变量组合的回归方 X= X21 程中,挑选一个最优者。②逐次别除法。即从包含全部自变 量的回归方程中,逐次剔除影响不显著的自变量。③逐个引 进法。即从先引进一个自变量开始,把其他影响显著的自变 模型的参数也就是系数阵B,可以采用最小二乘法估 量逐个引进回归方程。④逐步回归法(有进有出法)。与方法 计:B=(X·X)'Y。回归系数b(G=1,2,…,K)表明当 ③类似,它也是从先引进一个自变量开始,按各自变量与因变 其他自变量保持不变的条件下,自变量x(=1,2,…,k)每 量的相关系数的大小,依次逐个引进回归方程。但不同的是 变动一个单位所引起的因变量Y的平均变动量。如以某种 当先引进的自变量由于后引进的自变量使它对于因变量影响 商品需求量为因变量Y,该商品的价格为自变量x1,消费者不显著时,则随时将它从回归方程中剔除。因此逐步回归的每 收入为自变量x2,假定利用样本数据进行最小二乘法估计,一步(包括引进一个自变量或从回归方程中剔除一个自变量) 则得到: 都要作t检验,以保证每次在引进新的显著的自变量之前,回 7=111.69-7.19x1+0.14x 归方程中只包含显著的自变量,直到没有显著的自变量可以 这表明当消费者收入不变时,商品价格每降低1元,该引人回归方程为止

第2章金融预测分析方法19 逐步回归分析法(Stepwise Regression Analysis (1)对因变量y的所有观测值作对数变换,即令Y= Method) ny,i=1,2,…,n,n是观测数据的个数。与x之间的关系 逐步回归的思路是先将各种可能的因素都当作自变量引 为: 入模型,然后定义一个“贡献”系数,再用贡献系数的大小,来 Y =A+Bx 判断影响的大小。 (2)按照使平方和Q=∑(Y-A-Bx)2=min的原则来 贡献系数D,,定义为因变量y与某个所研究的自变量x 确定回归系数A与B。 间的协方差平方云与x的平方差之比,即: (3)分别对A、B取反对数,得a=e,b=e,所求指数函数 D(o)=ri/ra 模型为y=ab。 逐步回归计算步骤可归纳为: (4)对于给定的x值,预测值y=ab。 第一步,通过初始相关矩阵R,=(r),求各自变量 2.双曲线模型。双曲线模型可以表示为y=a+b/x,其中 x,(i=1,…,m)的贡献系数: a>0,b>0。变量y单调下降,以y=a为渐近线。双曲线模型 D.(o)=ri/ra 常用于描述产品成本的变动规律。令X=1/x,双曲线模型变 第二步,在m个贡献系数中,找最大贡献系数: 为一元线性回归模型y=a+bX,模型不难求解。 D(o)maxD(o) 3.倒数曲线模型。倒数曲线模型的一般形式为y=x/(ax 第三步,规定一个指标系数Po,在一个具有n组数据的情 +b),其中a>0,b>0。倒数函数的特点是单调递增,但增长 况下,定义下述比较系数Po: 率逐步下降,函数以1/a为其增长极限。 .(n-3)D9 P%= 这种方法用于预测企业的利润变化较为有效。建立倒数 Txx -D(o) 函数模型的具体步骤为: 若有P。>Po,则自变量xu即为对y影响最大的量。上式 (1)将y=x/(ax+b)改写为1/y=a+b/x,对自变量x和因变 中,「n是y的方差。 量y作倒数变换:x'=l/x,y'=1/y,则得到y=a+bx'; 第四步,将)中第k列消去,得变换后的新协方阵 (2)按一元线性回归方程求得系数a,b进行预测。 R)=(),然后按上述方法继续计算。 4.柯布一格拉斯生产函数模型。生产函数是当今西方经济 学的一个重要概念。它表示在一定技术条件下,生产要素的某种 非线性回归预测法(Non-Linear Regression Predic- 组合同它可能生产的最大产出量之间的数量关系。这里的产出既 tion Method 可以是某段时间生产的数量,也可以是产出的价值量,如总产值 指用于经济预测分析的回归方程是一种曲线,如双曲线 或净产值。常见的二元生产函数的形式为: 和指数函数曲线等。严格地说,各经济变量之间的相互关系 y AL*K 应是非线性的,线性相关是非线性相关的一种特殊情况。当 即柯布一道格拉斯生产函数,其中A,:,B均为正参数,y表示 非线性程度较低时,可以用线性回归取得较为满意的效果。 产出量,L为投入的劳动量,K为投入的资本量。柯布一道格 从线性回归转为非线性回归,分析和计算都困难得多。幸运 拉斯生产函数可以用来预测企业发展趋势。建立柯布一道格 的是,不少常见的非线性回归问题可以转为线性回归问题来拉斯生产函数的具体步骤为: 求解。常用的几种模型有: (1)对两端取对数,得lny=lnA+alnL+BnK。令lny=Y, 1.指数函数模型。指数函数的一般形式为y=ab,这是a=n4,x1=lnL,x2=lnK,则有: 一种使用较广的预测模型。设自量x的观测值呈等距分布 Y a ax Bxz (时间序列即如此),若因变量y的观测值有随自变量x的观 (2)按二元线性回归方程的方法确定a、a、B。对a取反 测值的增加而单调增加(或单调下降)的趋势,且各期的增长 对数,得A=e,所求生产函数模型为: 率(或下降率)基本相等,则采用指数函数来拟合这些数据是 y ALK 较为合理的。我们可以通过在方程y=ab两边取对数的方法 5.多项式模型。参见“增长曲线预测法”条。 将它变换为线性形式: y ab" 自回归预测法(Auto-Regressive Prediction Method) Iny a xlnb 表1-2-2某市1988~1991年各月照明用电量单位:万度 Y Iny,A Ina,B Inb, 成 则有: 1988 1989 1990 1991 月 Y A Bx 74 52 57 67 67 这是一个一元线性回归模型。按一元线性回归预测的方 52 59 59 64 法确定A与B的值,再根据x的值来预测y的值。建立指数函 数模型的具体步骤为:
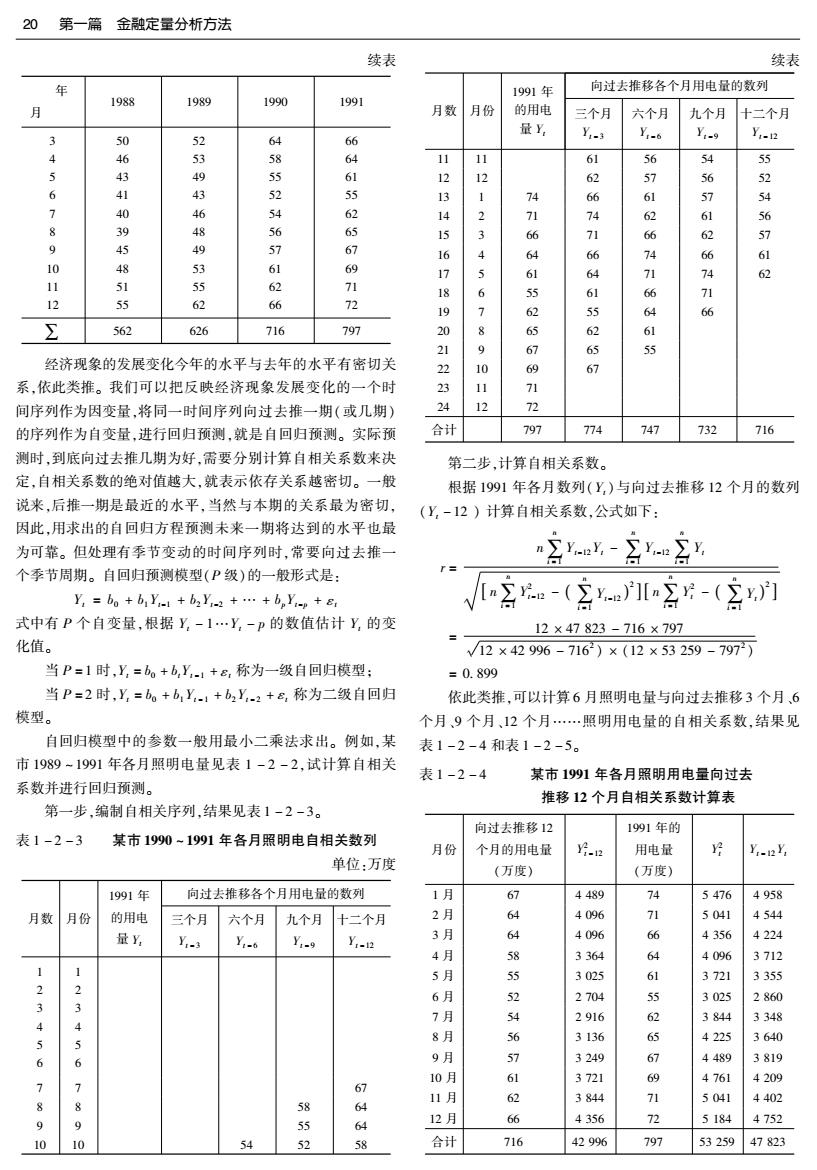
20 第一篇金融定量分析方法 续表 续表 1991年 向过去推移各个月用电量的数列 1988 1989 1990 1991 月数 月份 的用电 三个月 六个月 九个月 十二个月 量y, 50 52 66 Y-3 y.6 y-9 Y-2 4 11 11 61 6 54 55 5 39 5 61 12 57 6 41 13 1 51 4 7 6 62 8 39 4 5 65 156 3 6 9 49 66 10 学 4 74 6 53 61 69 5 74 11 51 5 62 71 12 55 62 66 72 Σ 562 626 716 797 1890 678 4164652679 26416465267 9 S415 经济现象的发展变化今年的水平与去年的水平有密切关 2 系,依此类推。我们可以把反映经济现象发展变化的一个时 23 11 71 间序列作为因变量,将同一时间序列向过去推一期(或几期) 24 12 72 的序列作为自变量,进行回归预测,就是自回归预测。实际预 合计 797 774 747 732 716 测时,到底向过去推几期为好,需要分别计算自相关系数来决 第二步,计算自相关系数。 定,自相关系数的绝对值越大,就表示依存关系越密切。一般 根据1991年各月数列(Y,)与向过去推移12个月的数列 说来,后推一期是最近的水平,当然与本期的关系最为密切, (Y-12)计算自相关系数,公式如下: 因此,用求出的自回归方程预测未来一期将达到的水平也最 为可靠。但处理有季节变动的时间序列时,常要向过去推一 "月x-Ay 个季节周期。自回归预测模型(P级)的一般形式是: Y,bo +biYc+b2Y-2+.+bpyip+r √公-(ae]g-(2门 式中有P个自变量,根据Y,-1…Y,-p的数值估计Y,的变 12×47823-716×797 化值。 √12×42996-716)×(12×53259-797) 当P=1时,Y,=b。+b,Y1+8,称为一级自回归模型; =0.899 当P=2时,Y=b。+bY.1+b2y,-2+8,称为二级自回归 依此类推,可以计算6月照明电量与向过去推移3个月、6 模型。 个月、9个月、12个月…照明用电量的自相关系数,结果见 自回归模型中的参数一般用最小二乘法求出。例如,某 表1-2-4和表1-2-5。 市1989-1991年各月照明电量见表1-2-2,试计算自相关 表1-2-4 某市1991年各月照明用电量向过去 系数并进行回归预测。 推移12个月自相关系数计算表 第一步,编制自相关序列,结果见表1-2-3。 向过去推移12 1991年的 表1-2-3 某市1990~1991年各月照明电自相关数列 月份 个月的用电量 片.2 用电量 Yi-12Y 单位:万度 (万度) (万度) 1991年 向过去推移各个月用电量的数列 1月 67 4489 74 5476 4958 月数 月份 的用电 三个月 六个月 九个月 十二个月 2月 64 4096 71 5041 4544 量Y y- Y-6 Y-2 3月 64 4096 4356 4224 4月 58 3364 6 4096 3712 5月 5 3025 3721 3355 6月 52 2704 55 3025 2860 3 3 7月 54 2916 62 3844 3348 4 4 5 5 8月 56 3136 65 4225 3640 6 6 9月 》 3249 67 4489 3819 4209 7 个 6 10月 61 3721 69 4761 11月 62 3844 71 5041 4402 58 9 9 5 64 12月 66 4356 72 5184 4752 10 10 54 58 合计 716 42996 797 53259 47823

第2章金融预测分析方法21 表1-2-5某市1988~1991年照明用电量自相关系数表 =61.85(万度) 1991年的用电量与向过去推 由上可见,所谓自回归预测就是利用回归分析的方法对 向过去推移月数 符号 移各月用电量的自相关系数 时间序列进行预测,这种方法简便,灵活,原始资料易于取得, 推移36个月的用电量 Y-36 0.816 在预测实践中有广泛的应用。 推移33个月的用电量 Y-38 0.401 推移30个月的用电量 Y-30 -0.672 封闭式移动回归预测法(Closed Moving Regression 推移27个月的用电量 Y:-n -0.514 Prediction Method)】 推移24个月的用电量 Y-24 0.876 这种预测方法是从既定的样本信息出发,进行两阶段回归 推移21个月的用电量 Y-24 0.472 Y,-1s 最后得到关于时间参数:的函数,即参数函数或参数复量。因此, 推移18个月的用电量 -0.585 推移15个月的用电量 参数随着时间的推移可自发地变化,但不能直接利用新的样本信 Y-5 -0.678 推移12个月的用电量 Y-2 息进行递推变化,故为封闭式预测方法。以下我们仅考虑只有一 0.899 推移9个月的用电量 Yi-9 0.364 个自变量的一元线性模型的动态估计,其形式为: 推移6个月的用电量 Y-6 -0.614 ,=àw+bx,t=0,1,2…p 推移3个月的用电量 Y-3 -0.345 时序资料为(x1,),(x2,2),…,(x70y70), 1991年的用电量 (xri,yri),…,(xr+p,yr+p)或(x,y),i=1,2…n,T+p 由表中资料可以看出,向过去推移12、24、36个月的照明 =n我们的任务是求取ao、6a。为此,第一步是确定ao、 用电量与1991年照明用电量向相关系数都相当高,这是因为 bo的形式,其次是需要ao、ia的时序数据ao,bo,然后以i 历年各月照明用电量的发展趋势和变动大致相同。 为自然变量进行回归,最后得到aw=ao,6o=6o,下面我 第三步,进行预测。由于1991年序列与向后推移12个月 们作具体分析: 的序列自相关系数最大,取一级回归模型进行预测,计算过程 1.确定ao6a的形式,一般设定它们为如下线性形式: 如下: d=@+B,bo=y+it 模型为: 立=bo+bY-n 2.求取ao、6o的时序数据a、b。有两种想法:一是 用最小二乘法估计参数: 把时间序列数据分割成若干段,对每一段进行回归,这样就可 月g只w-A(含) 以得到若干个a)、o;另一种是把时序数据进行嵌套式分 组,如将(x,y)分为如下P+1组: ge(会e小 (x1,y1),(2,y2)…(xy), (xy),(2,2)…(xy),(4y1), =797×42996-716×47823 12×42996-7162 (x1,y1),(2,2)(xJyr),(x1,y1),…(XToYTop) =8.0534 T+P=n然后对每组分别进行回归,则可得时序数据 ao、bmo 以-… 3.利用时序数据进行第二阶段回归及预测,对数据(:, ng-(公月 a,),(t,6,),t=0,1,…,p进行线性回归,最后得到a=ao= -12×47823-716×797 a+,io=io=y+t。至此,得到如下变参数模型: 12×42996-7162 y:=a(+60x =0.9782 =(a+B(t)+(y+(t)x 一级自回归模型为: 立,=8.0534+0.9782Y-e 马尔可夫预测法(Markov Predication Method) 预测1992年1月份的用电量为: 马尔可夫(A.A.Markov)是俄国的一位数学家。1907年 立1=8.0534+0.9782y-2 他发现某些随机事件的第n次试验结果,常决定于它的第(n -1)次试验结果。马尔可夫假定第(n-1)次转移过程中的转 =8.0534+0.9782×74 移概率不变,用来对物理学中的布朗运动作数学说明。这项 =80.4(万度) 原理于1923年由N.Wisnet发展成为一项数学模式,再经A. 预测1992年6月份的用电量为: N.Kolmagonov、W.Feller、W.Doebin等学者于1930~1940年 ,6=8.0534+0.9783Y6 间继续发展成为一项完整的随机过程理论,并把时间序列转 =8.0534+0.9782×55 移概率的链式称为马尔可夫链。马尔可夫预测法,就是利用