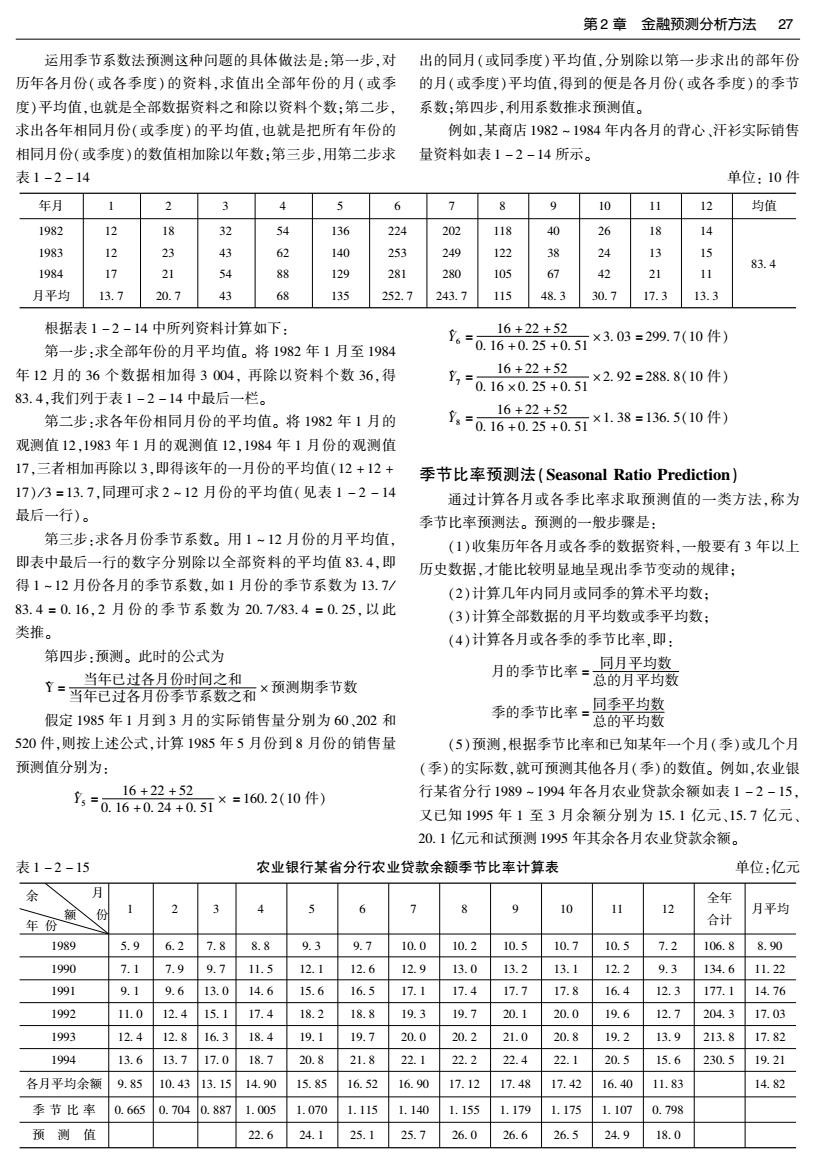
第2章金融预测分析方法27 运用季节系数法预测这种问题的具体做法是:第一步,对出的同月(或同季度)平均值,分别除以第一步求出的部年份 历年各月份(或各季度)的资料,求值出全部年份的月(或季 的月(或季度)平均值,得到的便是各月份(或各季度)的季节 度)平均值,也就是全部数据资料之和除以资料个数:第二步,系数:第四步,利用系数推求预测值。 求出各年相同月份(或季度)的平均值,也就是把所有年份的 例如,某商店1982-1984年内各月的背心、汗衫实际销售 相同月份(或季度)的数值相加除以年数:第三步,用第二步求 量资料如表1-2-14所示。 表1-2-14 单位:10件 年月 1 2 5 6 > 8 9 10 11 12 均值 1982 的 18 32 54 136 224 202 118 0 26 18 14 1983 12 23 43 62 140 253 249 122 38 24 13 15 1984 17 21 54 88 129 83.4 281 280 105 少 42 21 11 月平均 13.7 20.7 43 68 135 252.7 243.7 115 48.3 30.7 17.3 13.3 根据表1-2-14中所列资料计算如下: 16+22+52 -×3.03=299.7(10件) 第一步:求全部年份的月平均值。将1982年1月至1984 。=0.16+0.25+0.5 年12月的36个数据相加得3004,再除以资料个数36,得 16+22+52 -0.16x02540,×2.92=28.8(10件) 83.4,我们列于表1-2-14中最后一栏。 16+22+52 第二步:求各年份相同月份的平均值。将1982年1月的 =016+025+0.5×1.38=136.5(10件) 观测值12,1983年1月的观测值12,1984年1月份的观测值 17,三者相加再除以3,即得该年的一月份的平均值(12+12+ 季节比率预测法(Seasonal Ratio Prediction) 17)/3=13.7,同理可求2-12月份的平均值(见表1-2-14 通过计算各月或各季比率求取预测值的一类方法,称为 最后一行)。 季节比率预测法。预测的一般步骤是: 第三步:求各月份季节系数。用1~12月份的月平均值, (1)收集历年各月或各季的数据资料,一般要有3年以上 即表中最后一行的数字分别除以全部资料的平均值83.4,即 历史数据,才能比较明显地呈现出季节变动的规律: 得1~12月份各月的季节系数,如1月份的季节系数为13.7/ (2)计算几年内同月或同季的算术平均数: 83.4=0.16,2月份的季节系数为20.7/83.4=0.25,以此 (3)计算全部数据的月平均数或季平均数: 类推。 (4)计算各月或各季的季节比率,即: 第四步:预测。此时的公式为 当年已过各月份时间之和 月的季节比率= 同月平均数 1=当年已过名月份季节系数之和×预测期季节数 总的月平均数 假定1985年1月到3月的实际销售量分别为60、202和 季的季节比率=同季平均数 总的平均数 520件,则按上述公式,计算1985年5月份到8月份的销售量 (5)预测,根据季节比率和已知某年一个月(季)或几个月 预测值分别为: (季)的实际数,就可预测其他各月(季)的数值。例如,农业银 16+22+52 -016+024+0.5×=160.2(10件) 行某省分行1989~1994年各月农业贷款余额如表1-2-15, 又已知1995年1至3月余额分别为15.1亿元、15.7亿元 20.1亿元和试预测1995年其余各月农业贷款余额。 表1-2-15 农业银行某省分行农业贷款余额季节比率计算表 单位:亿元 余 全年 额 8 9 10 11 12 月平均 年份 合计 1989 5.9 6.2 8.8 9.3 9.7 10.0 10.2 10.5 10.7 10.5 7.2 106.8 8.90 1990 7.1 7.9 9. 11.5 12.1 12.6 12.9 13.0 13.2 13.1 12.2 9.3 134.6 11.22 1991 9.1 9.6 13.0 14.6 15.6 16.5 17.1 17.4 17.7 17.8 16.4 12.3 177.1 14.76 1992 11.0 12.4 15. 17.4 18.2 18.8 19.3 19.7 20.1 20.0 19.6 12.7 204.3 17.03 1993 12.4 12.8 16.3 18.4 19.1 19.7 20.0 20.2 21.0 20.8 19.2 13.9 213.8 17.82 1994 13.6 13.7 17.0 18.7 20.8 21.8 22.1 22.2 22.4 22.1 20.5 15.6 230.5 19.21 各月平均余额 9.85 10.43 13.15 14.90 15.85 16.52 16.90 17.12 17.48 17.42 16.40 11.83 14.82 季节比率 0.665 0.704 .887 1.005 1.070 1.115 L.140 1.155 1.179 1.175 1.107 0.798 预测值 22.6 24.1 25.1 25.7 26.0 26.6 26.5 24.9 18.0
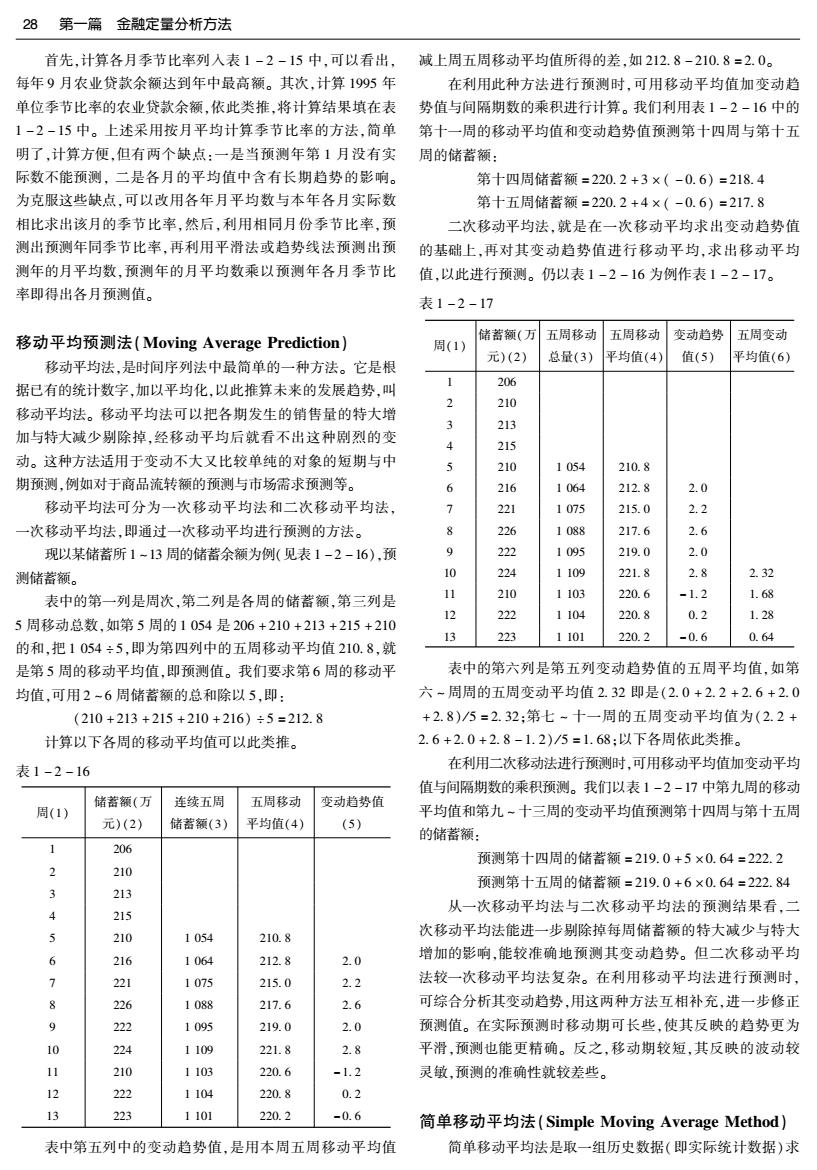
28 第一篇金融定量分析方法 首先,计算各月季节比率列入表1-2-15中,可以看出, 减上周五周移动平均值所得的差,如212.8-210.8=2.0。 每年9月农业贷款余额达到年中最高额。其次,计算1995年 在利用此种方法进行预测时,可用移动平均值加变动趋 单位季节比率的农业贷款余额,依此类推,将计算结果填在表 势值与间隔期数的乘积进行计算。我们利用表1-2-16中的 1-2-15中。上述采用按月平均计算季节比率的方法,简单 第十一周的移动平均值和变动趋势值预测第十四周与第十五 明了,计算方便,但有两个缺点:一是当预测年第1月没有实 周的储蓄额: 际数不能预测,二是各月的平均值中含有长期趋势的影响。 第十四周储蓄额=220.2+3×(-0.6)=218.4 为克服这些缺点,可以改用各年月平均数与本年各月实际数 第十五周储蓄额=220.2+4×(-0.6)=217.8 相比求出该月的季节比率,然后,利用相同月份季节比率,预 二次移动平均法,就是在一次移动平均求出变动趋势值 测出预测年同季节比率,再利用平滑法或趋势线法预测出预 的基础上,再对其变动趋势值进行移动平均,求出移动平均 测年的月平均数,预测年的月平均数乘以预测年各月季节比 值,以此进行预测。仍以表1-2-16为例作表1-2-17。 率即得出各月预测值。 表1-2-17 移动平均预测法(Moving Average Prediction) 储蓄额(万 五周移动 五周移动 变动趋势 五周变动 周(1) 元)(2) 总量(3) 平均值(4)》 值(5) 平均值(6) 移动平均法,是时间序列法中最简单的一种方法。它是根 据已有的统计数字,加以平均化,以此推算未来的发展趋势,叫 206 210 移动平均法。移动平均法可以把各期发生的销售量的特大增 213 加与特大减少剔除掉,经移动平均后就看不出这种剧烈的变 4 215 动。这种方法适用于变动不大又比较单纯的对象的短期与中 5 210 1054 210.8 期预测,例如对于商品流转额的预测与市场需求预测等。 6 216 1064 212.8 2.0 移动平均法可分为一次移动平均法和二次移动平均法, 7 221 1075 215.0 2.2 次移动平均法,即通过一次移动平均进行预测的方法。 8 226 1088 217.6 2.6 现以某储蓄所1-13周的储蓄余额为例(见表1-2-16).预 9 222 1095 219.0 2.0 测储蓄额。 10 224 1109 221.8 2.8 2.32 表中的第一列是周次,第二列是各周的储蓄额,第三列是 11 210 1103 220.6 -1.2 1.68 12 222 1104 220.8 0.2 1.28 5周移动总数,如第5周的1054是206+210+213+215+210 13 223 1101 220.2 -0.6 0.64 的和,把1054÷5,即为第四列中的五周移动平均值210.8,就 是第5周的移动平均值,即预测值。我们要求第6周的移动平 表中的第六列是第五列变动趋势值的五周平均值,如第 均值,可用2-6周储蓄额的总和除以5,即: 六~周周的五周变动平均值2.32即是(2.0+2.2+2.6+2.0 (210+213+215+210+216)÷5=212.8 +2.8)/5=2.32:第七~十一周的五周变动平均值为(2.2+ 计算以下各周的移动平均值可以此类推。 2.6+2.0+2.8-1.2)/5=1.68:以下各周依此类推。 表1-2-16 在利用二次移动法进行预测时,可用移动平均值加变动平均 值与间隔期数的乘积预测。我们以表1-2-17中第九周的移动 储蓄额(万 连续五周 五周移动 变动趋势值 周(1) 平均值和第九~十三周的变动平均值预测第十四周与第十五周 元)(2) 储蓄额(3) 平均值(4) (5) 的储蓄额: 206 预测第十四周的储蓄额=219.0+5×0.64=222.2 210 预测第十五周的储蓄额=219.0+6×0.64=222.84 3 213 215 从一次移动平均法与二次移动平均法的预测结果看,二 5 210 1054 210.8 次移动平均法能进一步剔除掉每周储蓄额的特大减少与特大 6 216 1064 212.8 2.0 增加的影响,能较准确地预测其变动趋势。但二次移动平均 7 221 1075 215.0 2.2 法较一次移动平均法复杂。在利用移动平均法进行预测时, 8 226 1088 217.6 2.6 可综合分析其变动趋势,用这两种方法互相补充,进一步修正 9 222 1095 219.0 2.0 预测值。在实际预测时移动期可长些,使其反映的趋势更为 10 224 1109 221.8 2.8 平滑,预测也能更精确。反之,移动期较短,其反映的波动较 210 1103 220.6 -1.2 灵敏,预测的准确性就较差些。 222 1104 220.8 0.2 13 223 1101 220.2 -0.6 简单移动平均法(Simple Moving Average Method) 表中第五列中的变动趋势值,是用本周五周移动平均值 简单移动平均法是取一组历史数据(即实际统计数据)求

第2章金融预测分析方法 29 其平均值,而以该平均值作为下期的预测值。其预测模型为: ∑atix- (2) S1=+1+…+ (1) n 式中a,是与x相对应的权值。应满足的条件是: 也可简写为: S1= 1了x ∑aal=n n台 例:某工商银行支行1982~1991年年末贷款余额如表1- 式中,S1一第1+1期(预测期)的预测值: 2-18。分别用简单移动平均法和加权移动平均法计算其预 x一第i期的实际值: 测值。表中n=3,权数分别为0.5,1、1.5。从表1-2-18中 i—1,2,…,n 将两种方法的预测结果进行比较,可以看出,采用加权移动平 nm一平均值的数据个数。 均法,只要权值a选得合适,其预测值会更加接近实际情况。 从模型(1)可以看出,要求出t+1期的预测值,必须要有 表1-2-18 n个距预测期最近的实际数据值。n值是模型中的重要参数, 简单移动平 加权移动平 它的选择取决于数据的波动变化和实际数据量的多少。如果 年 度 年末贷款余额 均法预测值 均法预测值 波动不大,收集的实际数据较多,这时可选用较大的n值,n值 1982 200 愈大,则随机波动的削除效果愈好,就可显示事物发展趋势; 1983 210 如果波动较大,提取的实际数据又较少,可选用较小的n值, 1984 230 这样预测值随波动变化反应较为灵敏。n值可在6~200范围 1985 250 213.33 218.33 内选用。 1986 220 230.00 236.67 根据(1)式可推导出第:期的移动平均值为: 1987 240 233.33 231.67 8=h+a+…+) 1988 260 236.67 235.00 1989 280 240.00 246.67 将上式代入(1)式,则1+1期的预测值模型可简化为: 1990 270 260.00 266.67 S1=S+-✉ (2) 1991 300 270.00 271.67 nn 从(2)式可以看出,移动平均法的S,:预测值是前一期(: 总的来说,简单移动平均法和加权移动平均法,方法简 单,易于掌握。但需要数据量大,准确程度有限。因此,这些 期)预测值S,加上一个修正值喜-“。当n越大,修正值会 方法一般多用于经济领域的短期预测。 愈小,修正的作用愈来愈弱,预测曲线也会愈平滑。 这种方法只要有历史数据,就比较简单,易于掌握。但这 几何移动平均法(Geometric Moving Average Method) 种方法的预测结果准确度较差,预测值一般是滞后于实际值, 几何移动平均法是平滑预测法的一种,即是修匀时间序 存在较大偏差,所以一般用于短期经济预测。 列的一种方法。所谓几何移动平均,就是将第1期的n项移动 几何平均数作为第1+1期的预测值,即:设一数列为Y,Y2, 一次移动平均法(Primary Moving Average Method) …,Y。: 见“移动平均预测法”条。 l=M2=Y.·Y…Y-1 一般来说,当金融现象的发展水平大体上每期按相同的 二次移动平均法(Secondary Moving Average Method) 增长率变化时,用几何移动平均法预测较为合适。 见“移动平均预测法”条。 例如:1994年农业银行某省分行储蓄存款分月余额如表 1-2-19第2栏所示,移动期为3期,其加权数分别为0.5、1 加权移动平均法(Weighted Moving Average Method) 和1.5。 一股说来,距预测值愈近的数据对预测值影响愈大,愈远 表1-2-19 的数据则影响愈小。简单移动平均法是将历史数据不管其距 三期移动 三期移动 三期加 预测期远近都同等看待,取简单的平均值,这不完全符合事物 相对误 相对误 月份 余额 平均数预 权移动 几何平均 发展的规律。而加权移动平均法是根据数据距预测期的远近 差(%)》 平均数 差(%) 测值 数预测值 预测值 而给予不同的权值,以反映其不同的预测作用,距预测期近的 (1) (2) (3) (4) (5) (6) (7) 作用大,其权值也大,相反则权值小。其模型如下: 14.9 S4=+all+…+a1 (1 2 15.8 (1)式还可以写成:
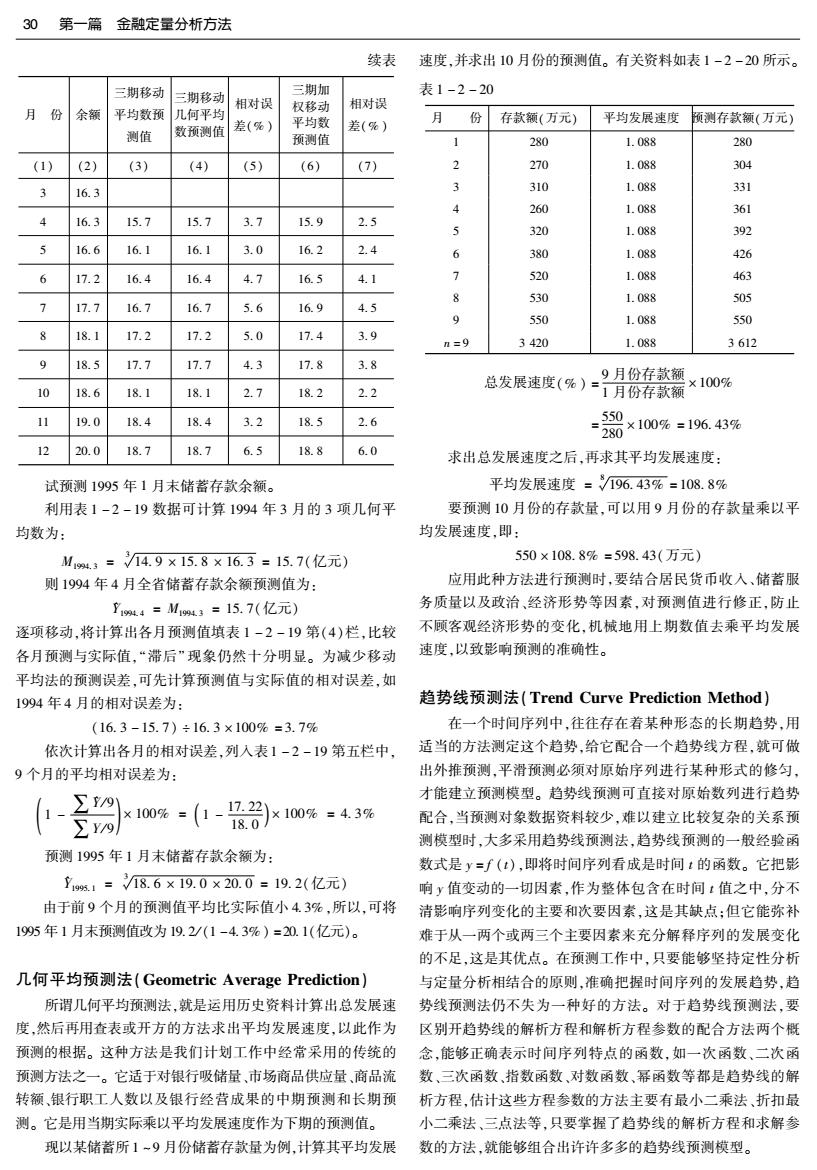
30 第一篇金融定量分析方法 续表 速度,并求出10月份的预测值。有关资料如表1-2-20所示。 三期移动 三期移动 三期加 表1-2-20 相对误 相对误 月份 余额 平均数预 几何平均 权移动 平均数 夕 份 存款额(万元) 平均发展速度 预测存款额(万元) 测值 数预测值 差(%) 差(%) 预测值 280 1.088 280 (1) (2) (3) (4) (5) (6) (7) 270 1.088 304 3 16.3 3 310 1.088 331 4 260 1.088 361 4 16.3 15.7 15.7 3.7 15.9 2.5 5 320 1.088 392 16.6 16.1 16.1 3.0 16.2 2.4 6 380 1.088 426 6 17.2 16.4 16.4 4.7 16.5 4.1 7 520 1.088 463 8 530 1.088 505 7 17.7 16.7 16.7 5.6 16.9 4.5 9 550 1.088 550 8 18.1 17.2 17.2 5.0 17.4 3.9 n=9 3420 1.088 3612 9 18.5 17.7 17.7 4.3 17.8 3.8 9月份存款额 ×100% 10 18.6 18.1 18.1 2.7 18.2 2.2 总发展速度(%)=1月份存款额 11 19.0 18.4 18.4 3.2 18.5 2.6 550 ×100%=196.43% 280 12 20.0 18.7 18.7 6.5 18.8 6.0 求出总发展速度之后,再求其平均发展速度: 试预测1995年1月末储蓄存款余额。 平均发展速度=/196.43%=108.8% 利用表1-2-19数据可计算1994年3月的3项几何平 要预测10月份的存款量,可以用9月份的存款量乘以平 均数为: 均发展速度,即: M1m.3=14.9×15.8×16.3=15.7(亿元) 550×108.8%=598.43(万元) 则1994年4月全省储蓄存款余额预测值为: 应用此种方法进行预测时,要结合居民货币收入、储蓄服 Y1944=M1994.3=15.7(亿元) 务质量以及政治、经济形势等因素,对预测值进行修正,防止 逐项移动,将计算出各月预测值填表1-2-19第(4)栏,比较 不顾客观经济形势的变化,机械地用上期数值去乘平均发展 各月预测与实际值,“滞后“现象仍然十分明显。为减少移动 速度,以致影响预测的准确性。 平均法的预测误差,可先计算预测值与实际值的相对误差,如 1994年4月的相对误差为: 趋势线预测法(Trend Curve Prediction Method) (16.3-15.7)÷16.3×100%=3.7% 在一个时间序列中,往往存在着某种形态的长期趋势,用 依次计算出各月的相对误差,列入表1-2-19第五栏中, 适当的方法测定这个趋势,给它配合一个趋势线方程,就可做 9个月的平均相对误差为: 出外推预测,平滑预测必须对原始序列进行某种形式的修匀, 才能建立预测模型。趋势线预测可直接对原始数列进行趋势 10%=(1-2x10%=43% 配合,当预测对象数据资料较少,难以建立比较复杂的关系预 测模型时,大多采用趋势线预测法,趋势线预测的一般经验函 预测1995年1月末储蓄存款余额为: 数式是y=∫(),即将时间序列看成是时间t的函数。它把影 立9%.1=18.6×19.0×20.0=19.2(亿元) 响y值变动的一切因素,作为整体包含在时间1值之中,分不 由于前9个月的预测值平均比实际值小43%,所以,可将 清影响序列变化的主要和次要因素,这是其缺点:但它能弥补 1995年1月末预测值改为19.2/(1-4.3%)=20.1(亿元)。 难于从一两个或两三个主要因素来充分解释序列的发展变化 的不足,这是其优点。在预测工作中,只要能够坚持定性分析 几何平均预测法(Geometric Average Prediction)】 与定量分析相结合的原则,准确把握时间序列的发展趋势,趋 所谓几何平均预测法,就是运用历史资料计算出总发展速 势线预测法仍不失为一种好的方法。对于趋势线预测法,要 度,然后再用查表或开方的方法求出平均发展速度,以此作为 区别开趋势线的解析方程和解析方程参数的配合方法两个概 预测的根据。这种方法是我们计划工作中经常采用的传统的 念,能够正确表示时间序列特点的函数,如一次函数、二次函 预测方法之一。它适于对银行吸储量、市场商品供应量、商品流 数、三次函数、指数函数、对数函数、幂函数等都是趋势线的解 转额、银行职工人数以及银行经营成果的中期预测和长期预 析方程,估计这些方程参数的方法主要有最小二乘法、折扣最 测。它是用当期实际乘以平均发展速度作为下期的预测值。 小二乘法、三点法等,只要掌握了趋势线的解析方程和求解参 现以某储蓄所1~9月份储蓄存款量为例,计算其平均发展 数的方法,就能够组合出许许多多的趋势线预测模型
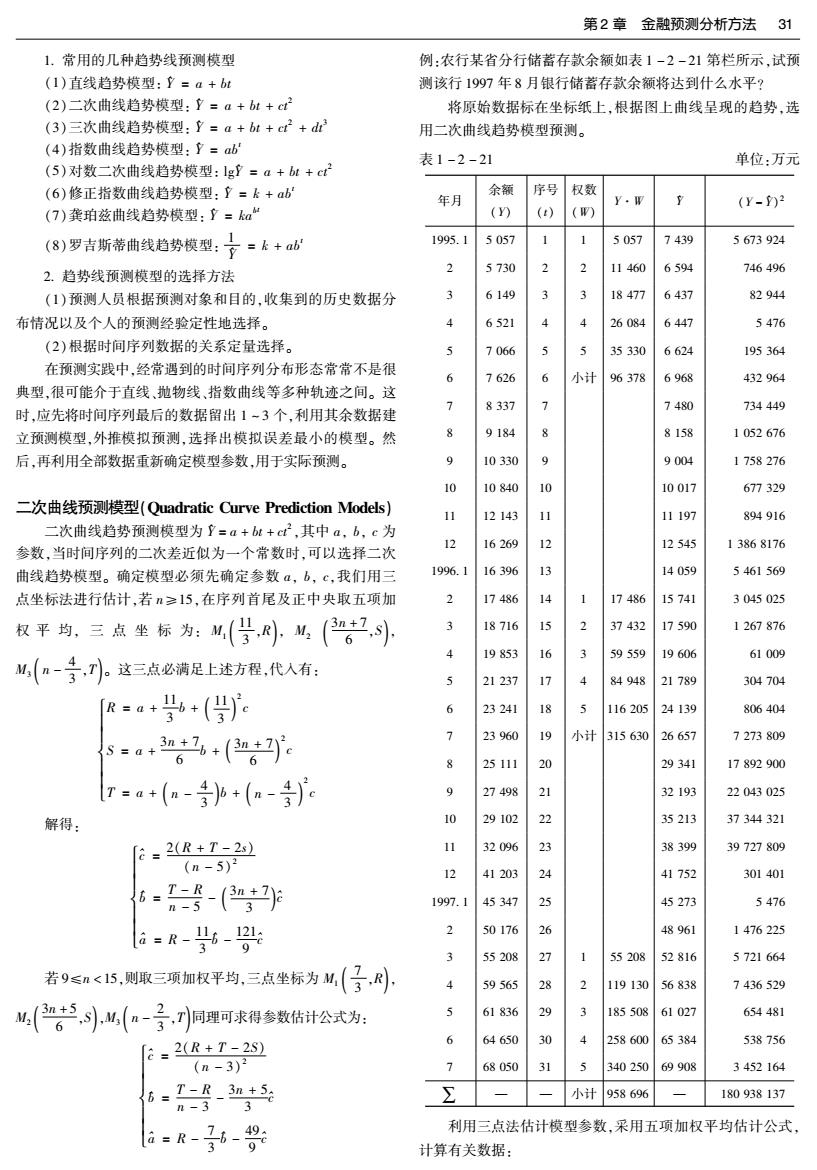
第2章金融预测分析方法31 1.常用的几种趋势线预测模型 例:农行某省分行储蓄存款余额如表1-2-21第栏所示,试预 (1)直线趋势模型:立=a+bt 测该行1997年8月银行储蓄存款余额将达到什么水平? (2)二次曲线趋势模型:Y=a+bt+c2 将原始数据标在坐标纸上,根据图上曲线呈现的趋势,选 (3)三次曲线趋势模型:了=a+bt+c2+d 用二次曲线趋势模型预测。 (4)指数曲线趋势模型:了=ab 表1-2-21 单位:万元 (5)对数二次曲线趋势模型:lg=a+bt+ct2 (6)修正指数曲线趋势模型:了=k+ab 余额 序号 权数 年月 y·W (Y-2 (7)龚珀兹曲线趋势模型:立=ka“ () (t) (W) (8)罗吉斯蒂尚线趋势模型:了=k+心 1995.1 5057 5057 7439 5673924 2.趋势线预测模型的选择方法 2 5730 11460 6594 746496 (1)预测人员根据预测对象和目的,收集到的历史数据分 3 6149 3 3 18477 6437 82944 布情况以及个人的预测经验定性地选择。 4 6521 26084 6447 5476 (2)根据时间序列数据的关系定量选择。 7066 35330 6624 195364 在预测实践中,经常遇到的时间序列分布形态常常不是很 6 7626 6 小计 96378 6968 432964 典型,很可能介于直线、抛物线、指数曲线等多种轨迹之间。这 1 8337 > 7480 734449 时,应先将时间序列最后的数据留出1-3个,利用其余数据建 立预测模型,外推模拟预测,选择出模拟误差最小的模型。然 8 9184 8158 1052676 后,再利用全部数据重新确定模型参数,用于实际预测。 9 10330 9 9004 1758276 10 10840 10 10017 677329 二次曲线预测模型(Quadratic Curve Prediction Models) 11 12143 11 11197 894916 二次曲线趋势预测模型为Y=a+bt+c2,其中a,b,c为 参数,当时间序列的二次差近似为一个常数时,可以选择二次 12 16269 12 12545 13868176 曲线趋势模型。确定模型必须先确定参数a,b,c,我们用三 1996.1 16396 13 14059 5461569 点坐标法进行估计,若n≥15,在序列首尾及正中央取五项加 2 17486 14 1 17486 15741 3045025 权平均,三点坐标为:(兮R,M(。 3 18716 15 37432 17590 1267876 4 19853 16 59559 19606 61009 M(n-子,T。这三点必满足上述方程,代人有: 5 21237 17 4 84948 21789 304704 Ra+号+(传e 6 23241 18 5 116205 24139 806404 7 +”。+( 23960 19 小计315630 26657 7273809 S a+ 8 25111 20 29341 17892900 r=a+(n-b+(n-子)e 9 27498 32193 22043025 解得: 10 29102 22 35213 37344321 「:=2R+T-2s) 11 32096 23 38399 39727809 (n-5)2 2 41203 24 41752 301401 6--(y 1997.1 45347 25 45273 5476 a=R-5-4 2 50176 26 48961 1476225 3 55208 27 55208 52816 5721664 若9≤n<15,则取三项加权平均,三点坐标为M,(子R, 59565 28 119130 56838 7436529 4(。苧小,4(a-子同理可求得参数估计公式为: 5 61836 29 3 185508 61027 654481 [:=2(R+T-2S) 6 64650 30 258600 65384 538756 (n-3)2 7 68050 31 34025069908 3452164 6=T-R_3n+5 小计 958696 180938137 n-33 6=R-子-g: 利用三点法估计模型参数,采用五项加权平均估计公式, 计算有关数据: