
12第一篇金融定量分析方法 F=P(1+i)+4(1+i)'-i+d+@ 永续年金(Perpetual Annuity) 2 2 见“永久年金”条。 2.等比变动。每期发生的年金分别是A,Ag,Ag,…。 当g>1时,年金是递增的:当0<g<1时,年金是递减的。此 展延年金(Extend Annuity)】 时普通年金复利现值和终值的计算方法是: 设每期发生年金是A1,A2,…,A,共连续1期。计算第 p++*+ (t+i) 一次支付的n期前的现值,或计算最后一次支付的n期后的终 值都叫做展延年金,亦称递延年金。每期发生的年金可以是 1- (1+i) 等额的也可以是变额的。 *1-4 1.n期后发生,每期发生年金是A1,A2,…,A,共连续 t期。 =A1-1+)二 1+i-g F=P(1+)' =A1+)-g 1+i-g 3.不规则变动。每期发生的年金分别是A,A2,A…,此 图1-1-6 时普通年金复利现值和终值计算公式分别为: (1)普通展延年金的现值,如图1-1-6: A3 A A2 A。 A. P=- =1+)m+(1+i)m+…+1+) =∑4 =∑ (1+) 台(1+i)可 F=A(1+)+A,(1+i)2+A(1+)3+…+A, = 4(1+) 图1-1-7 (2)期初展延年金的现值,如图1-1-7: 永久年金(Perpetual Annuity) A2 A 亦称永续年金。如果年金的期数永远继续,即期数t→ P=0++a+i)m+…+a+m 0,则称永久年金。 A 1.永久年金终值。普通年金复利终值是: 名(1+) F=A1+)-1 2.每期发生年金A1,A2,…A,共连续1期,展延n期。 i 因为1+i>1,所以永久年金终值是: AA2A3A (年金) C limF limA (1i)-1= 23… ,十1+2…什n(期数) 小x i 即永久年金终值是发散的。 图1-1-8 2.永久年金现值。普通年金复利现值是: (1)普通展延年金终值,如图1-1-8: P=A1-(1+) F=A1(1+i)-+A(1+i)-2+…+A,(1+i)“ 因为1+i>1,所以永久年金现值是: =∑A(1+i)可 D=回P=-=4 i A1A2A3A4A 〔年金) 同样方法可求得期初永久年金现值是: 十十十十十十 D=Al+i 0123…1-1t十1…t十n(期数) 有些永久性资金,就是设立一笔基金D,每期提取年金A 图1-1-9 =D作为奖金,年金可以永远按期提取,即每次提取的奖金额 (2)期初展延年金的终值,如图1-1-9: 是基金D每期的利息,而基金D永远保持不变。 F=A1(1+i)"”+A2(1+i)1+…+A,(t+i)1

第1章货币时间价值方法13 =∑A(1+i 计算的单利。因此,每年应提取的偿债基金公式为: i 式中,一复利率。 F=60+i-+co 偿债基金(Sinking Fund) 复利定价模型(Compound Interest Pricing Model) 偿债基金是指利用复利贷款时,在项目建成投产后,每年 从表1-1-14中我们可以知道美国国库券的复利方法是 按规定期限提取一笔偿债基金,以备按期偿还到期的贷款。 半年期收益率(y),而按天计的信用证的复利方法是天收益率 偿债基金的计算公式为: (用b表示),并且一年按360天计而不是365天。因为我们假 i 定最初的投资额相同,所以证券价格P在所有的表示中都是 F=F.(1+i)°-1 相同的。因此,适当的定价方程为: 式中,F—每年应提取的偿债基金: 国库券: F.一未来偿债总额; P= Par, i—一贷款年复利率: 、2/236 m一期望年限数; 21 i 365日信用证: 一偿债基金系数,表示在一定的年复利率 (1+)“-1 P= Pars 条件下,偿还贷款每年应提取的基金数额占未来偿债总额的 + 比例。它是年金终值系数的倒数。 因为在这个例子中,假定两种证券各自都投资$50000,那就 根据投资贷款的还款方式不同,偿债基金的计算方法有 本利一次归还法、分期归还法和分期付息法。 要看哪一种证券最后的偿还额最大。从面值的角度审视定价 1.本利一次归还法。它是按照贷款期限,在期满后一次 方程,并且注意这是6个月期的证券(t=182),可得: 国库券: 归还本息的方法。N年末归还的本利和就是投资贷款数额的 复利终值,计算公式为: F。=Co(1+i)“ 365日信用证: 式中,F.一投资贷款的本利和; C。一投资贷款的数额: =P1+) 一年复利率; 式中,Pay一按半年复利计算在期末应偿还的金额: n一贷款年限。 Parb一以一年360天计按天复利在期末应偿还的金额: 2.分期归还法。它一般是指银行贷款或利用外资采用每 P—一今天支付的价格: 年归还固定数额,期满本利和一次结算的方式。采用这种偿 一半年复利的利率: 债办法,应根据贷款总额的利率计算应偿还的本息,扣除每年 b—按一年360天计按天复利的利率。 还款的复利终值,然后计算最后一年的还款数额,其计算公 在本例中,y=b=6%。如计算这两种金融投资的未来价 式为: 值,可得: Fn=Co(1+i)” Par,=S5000(1+0062xiea =S51496 2 B=B可+)°-- i Par.=s50001+9g06) =s51540 式中,C。一贷款总额: B—每年固定还款额; 表1-1-14 货币市场复利定价模型 F.一应偿还的贷款本利和: 复利方法 定价方程 用这种方法的证券 B.—定额还款的复利终值。 Discount(d) 由于最后一年偿还的贷款包括在清算数额中,故式中 P=Pm(-岛)UsTe町 年金系数应减去1,最后一年应偿还贷款额按下列公式计 Add -on or Money P=Para 算: Market (m) 1+器 Eurodollar CDs H=R.-B.=c(1+-B[1+-1- Makes discount or and- Bond equivalent (r) P=Par, 式中,H—最后一年应偿还的贷款。 1*360 on rate comparable to semiannual rates 3.分期付息法。其特点是每年付贷款利息,期末一次还 Para Not widely used outside Annual (a) 清本金。采用这种还款方式时,每年支付的利息是按贷款额 P=[1+a]05 of academia

14第一篇 金融定量分析方法 续表 注:4.括号中的字母表示利率,是以十进制表示的。 复利方法 定价方程 用这种方法的证券 b.P表示现行价格或最初贷款额,Par代表债券的面值或期末必须 偿还的数额,t指贷款期中的日历天数,d.m,r,ayb和c都代表各 Pary P=- U.S.Treasury Bonds, Scmi-annual(y) 2/2S 种复利方法中的利率。 Corporate Bonds c有时用360天而不是365 Par 因此,虽然报出的利率相同,但从银行信用证投资中所得 P=一 Bank securities Daily e‘b) and mortgages 款项要高$44,明显表示应选择银行信用证投资。由此,我们 可以看出报出的利率必须同时说明是哪种复利方法,否则利 Continuous (c) P=Paue·ee(w6s) Bank securities like CDs 率就是不精确的。 are used with options

第2章金融预测分析方法 15 第2章金融预测分析方法 金融预测分析方法(Method of Financial Forecasting Analysis),是指在既定的金融环境中,利用所掌握的资 料,经分析考证影响金融投资或经营管理过程中某一环节、某一变量的外在因素和内在因素,确定出相关因素 间的函数关系,建立起数学模型,运用模型对某一项金融投资,或者某一项金融业务的效益、前景或可能出现 的趋势进行预测的方法。金融预测分析在金融监管、金融经营运行乃至个人投资理财中广泛运用,在市场经 济下不可或缺。本章先从一般地预测方法和入手,介绍一系列预测分析工具,接下去是微观金融预测分析、宏 观金融预测分析或中观金融预测分析。 普通最小二乘法(Ordinary Least Squares) 2.二次曲线趋势模型参数的估计。 普通最小二乘法是用数理统计的方法为经验公式确定回 模型为: y a+bt+ct? 归参数的方法,利用该法确定的回归参数,能够保证实际值与 用普通最小二乘法导出的正规方程组为: 拟合值之差的平方和为最小。以直线方程y=a+bx为例说 ∑y=nm+b∑:+c∑f 明。设给定n个点(x,少),(x2,2),…,(x。,y)。那么, 对于平面上任意一条直线L: ∑n=a∑1+b∑r+c∑i y =a+bx ∑r=a∑2+b∑r+c∑t ,-(a+c,)了户就定量地描述了直线L跟这n个点的 联解这个方程组就可求出模型参数a,6,c。 3.三次曲线趋势模型参数的估计。 远近程度,这个量也可看成是ab的二元函数,记为Q(a,b): 模型为: Y a+bt er+di 0:含-a+a 用普通最小二乘法导出的正规方程组为: 要找到二个数a,b,使二元函数Q(a,b)在a=a,b=6时 ∑y=ma+b∑1+c∑F+d∑2 达到最小。由于Q(a,b)是n个平方和,所以“使Q(a,b)最 ∑n=a∑+b∑t+c∑+d∑i 小”的原则称为平方和最小原则,习惯上称为最小二乘原则。 ∑f=a∑r+b∑+c∑r+d∑i 依照最小二乘原则,利用微分学中的极值原理,即解二元 一次联立方程 ∑m=a∑r+b∑r+e∑r+d∑ 联解这个方程组就可求出a,bca。 =-2∑[y,-(a+bx,)]=0 4.指数曲线趋势模型参数的估计。 模型为: y=ab' ab =-2∑[y,-(a+bx)]x,=0 两边求自然对数lg=lga+lgb 就可找到a,6,即解出了a、b,这种方法就是普通最小二乘法。 对上式用普通最小二乘法导出的标准方程: 在趋势线预测中,只要用时间变量t代替自变量x,就可用 ∑lgy=nlga+lg∑! 普通最小二乘法估计模型参数。 1.直线趋势模型参数的估计。 ∑lgy-lg∑+lgb∑2 模型为: y a bt 联解这个方程组,先求出lga,lgb,然后利用反对数表或计 用普通最小二乘法导出的正规方程组为: 算器就可求出模型参数a,6。 例如:以全国农村信用社1984~1993年各项存款余额 ∑y=na+b∑l 为样本,预测1994年各项存款余额。计算结果如表1-2- ∑n=a∑t+b∑r 1。 联解这个方程组就可求出模型参数a,6
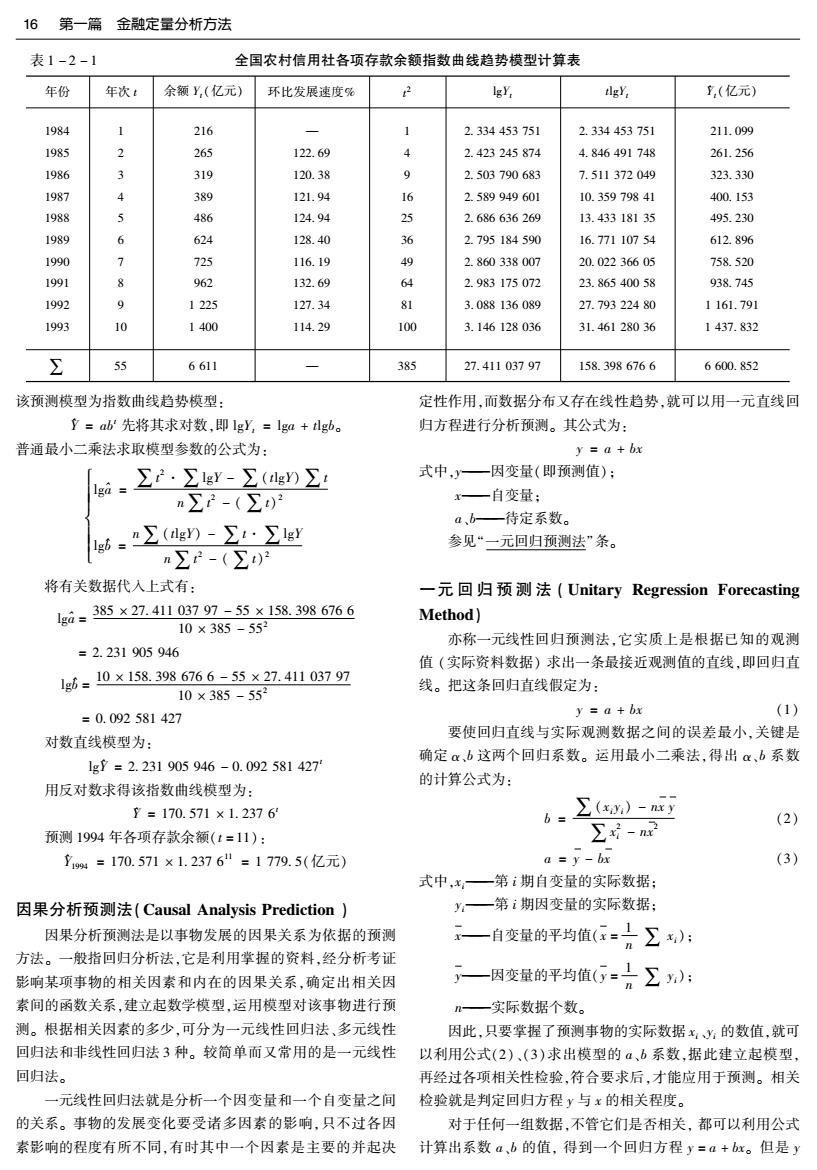
16 第一篇 金融定量分析方法 表1-2-1 全国农村信用社各项存款余额指数曲线趋势模型计算表 年份 年次t 余额Y,(亿元) 环比发展速度% 2 IgY, tlgY, ,(亿元) 1984 216 2.334453751 2.334453751 211.099 1985 2 265 122.69 4 2.423245874 4.846491748 261.256 1986 319 120.38 9 2.503790683 7.511372049 323.330 1987 389 121.94 16 2.589949601 10.35979841 400.153 1988 5 486 124.94 25 2.686636269 13.43318135 495.230 1989 6 624 128.40 哈 2.795184590 16.77110754 612.896 1990 7 725 116.19 49 2.860338007 20.02236605 758.520 1991 962 132.69 6 2.983175072 23.86540058 938.745 1992 9 1225 127.34 81 3.088136089 27.79322480 1161.791 1993 10 1400 114.29 100 3.146128036 31.46128036 1437.832 ∑ 55 6611 385 27.41103797 158.3986766 6600.852 该预测模型为指数曲线趋势模型: 定性作用,而数据分布又存在线性趋势,就可以用一元直线回 立=ab先将其求对数,即lgY,=lga+lgba 归方程进行分析预测。其公式为: 普通最小二乘法求取模型参数的公式为: y a +bx 、 ∑2·∑lgY-∑(gn∑: 式中,一因变量(即预测值): n∑2-(∑)2 x一自变量: a、b—待定系数。 n∑(lg)-∑·∑lgy 参见“一元回归预测法”条。 n∑r-(∑)2 将有关数据代入上式有: 一元回归预测法(Unitary Regression Forecasting 1ga=385×27.41103797-5×158.3986766 Method) 10×385-552 亦称一元线性回归预测法,它实质上是根据已知的观测 =2.231905946 值(实际资料数据)求出一条最接近观测值的直线,即回归直 1g6=10×158.3986766-55×27.41103797 10×385-552 线。把这条回归直线假定为: =0.092581427 y a+bx (1) 对数直线模型为: 要使回归直线与实际观测数据之间的误差最小,关键是 确定α,b这两个回归系数。运用最小二乘法,得出α、b系数 1gY=2.231905946-0.092581427 的计算公式为: 用反对数求得该指数曲线模型为: 7=170.571×1.23761 b= ∑(x)-ny (2) 预测1994年各项存款余额(t=11): ∑-n 立14=170.571×1.23761=1779.5(亿元) a y-bx (3) 式中,x,一第i期自变量的实际数据: 因果分析预测法(Causal Analysis Prediction) y:一第i期因变量的实际数据: 因果分析预测法是以事物发展的因果关系为依据的预测 一自变量的平均值(在=∑): 方法。一般指回归分析法,它是利用掌握的资料,经分析考证 影响某项事物的相关因素和内在的因果关系,确定出相关因 ,一因变量的平均值(=∑): 素间的函数关系,建立起数学模型,运用模型对该事物进行预 m—一实际数据个数。 测。根据相关因素的多少,可分为一元线性回归法、多元线性 因此,只要掌握了预测事物的实际数据xy:的数值,就可 回归法和非线性回归法3种。较简单而又常用的是一元线性 以利用公式(2)、(3)求出模型的a、b系数,据此建立起模型, 回归法。 再经过各项相关性检验,符合要求后,才能应用于预测。相关 一元线性回归法就是分析一个因变量和一个自变量之间 检验就是判定回归方程y与x的相关程度。 的关系。事物的发展变化要受诸多因素的影响,只不过各因 对于任何一组数据,不管它们是否相关,都可以利用公式 素影响的程度有所不同,有时其中一个因素是主要的并起决 计算出系数a、b的值,得到一个回归方程y=a+bx。但是y