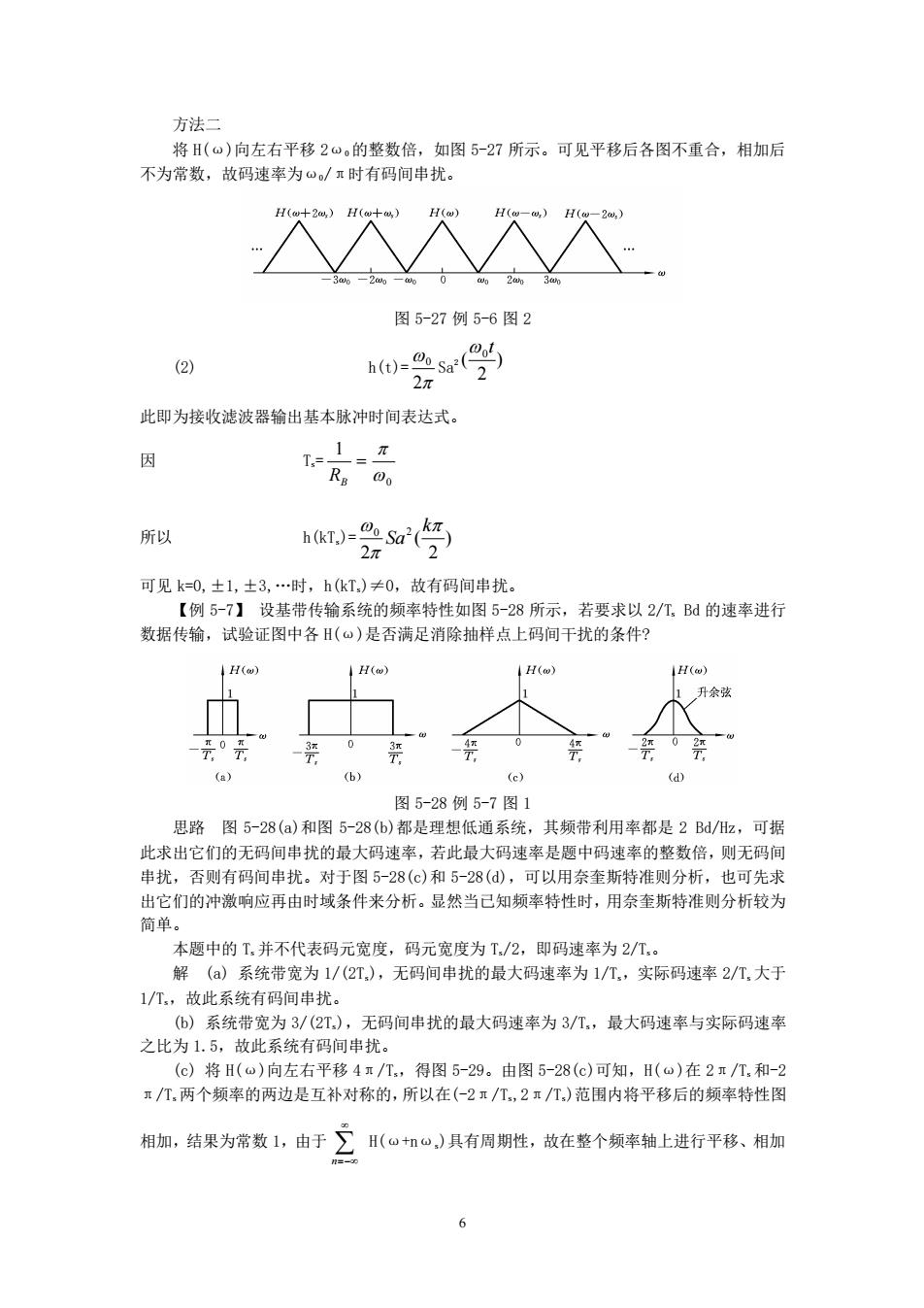
方法二 将H()向左右平移2@,的整数倍,如图5-27所示。可见平移后各图不重合,相加后 不为常数,故码速率为/时有码间串扰。 个入人入 图5-27例5-6图2 (2) -会s(学 此即为接收滤波器输出基本脉冲时间表达式。 1π Rg @o 所以 h-%sa(经) 2π 可见k=0,±1,士3,.时,h(kT,)≠0,故有码间串扰。 【例5-7】设基带传输系统的频率特性如图5-28所示,若要求以2/T.Bd的速率进行 数据传输,试验证图中各H(“)是否满足消除抽样点上码间干扰的条件? H() H(o) .口. 0 (a》 (6) (e) (d) 图5-28例5-7图1 思路图5-28(a)和图528(b)都是理想低通系统,其频带利用率都是2Bd/z,可据 此求出它们的无码间串扰的最大码速率,若此最大码速率是题中码速率的整数倍,则无码间 串扰,否则有码间串扰。对于图5-28(c)和5-28(),可以用奈奎斯特准则分析,也可先求 出它们的冲激响应再由时域条件来分析。显然当己知频率特性时,用奈奎斯特准则分析较为 简单。 本题中的T,并不代表码元宽度,码元宽度为T,/2,即码速率为2/T 解(a)系统带宽为1/(21,),无码间串扰的最大码速率为1/T。,实际码速率2/T,大于 1/T,故此系统有码间串扰。 (6)系统带宽为3/(2T,),无码间串扰的最大码速率为3/T,最大码速率与实际码速率 之比为1.5,故此系统有码间串扰。 (c)将H()向左右平移4/T.,得图5-29。由图5-28(C)可知,H()在2年/T.和-2 /T,两个频率的两边是互补对称的,所以在(-2个,2个,)范围内将平移后的频率特性图 相加,结果为常数1,由于∑(ω+n“,)具有周期性,故在整个频率轴上进行平移、相加 6
6 方法二 将 H(ω)向左右平移 2ω0 的整数倍,如图 5-27 所示。可见平移后各图不重合,相加后 不为常数,故码速率为ω0/π时有码间串扰。 图 5-27 例 5-6 图 2 (2) h(t)= 2 0 Sa2 ) 2 ( 0 t 此即为接收滤波器输出基本脉冲时间表达式。 因 Ts= 0 1 = RB 所以 h(kTs)= ) 2 ( 2 0 2 k Sa 可见 k=0,±1,±3,.时,h(kTs)≠0,故有码间串扰。 【例 5-7】 设基带传输系统的频率特性如图 5-28 所示,若要求以 2/Ts Bd 的速率进行 数据传输,试验证图中各 H(ω)是否满足消除抽样点上码间干扰的条件? 图 5-28 例 5-7 图 1 思路 图 5-28(a)和图 5-28(b)都是理想低通系统,其频带利用率都是 2 Bd/Hz,可据 此求出它们的无码间串扰的最大码速率,若此最大码速率是题中码速率的整数倍,则无码间 串扰,否则有码间串扰。对于图 5-28(c)和 5-28(d),可以用奈奎斯特准则分析,也可先求 出它们的冲激响应再由时域条件来分析。显然当已知频率特性时,用奈奎斯特准则分析较为 简单。 本题中的 Ts 并不代表码元宽度,码元宽度为 Ts/2,即码速率为 2/Ts。 解 (a) 系统带宽为 1/(2Ts),无码间串扰的最大码速率为 1/Ts,实际码速率 2/Ts 大于 1/Ts,故此系统有码间串扰。 (b) 系统带宽为 3/(2Ts),无码间串扰的最大码速率为 3/Ts,最大码速率与实际码速率 之比为 1.5,故此系统有码间串扰。 (c) 将 H(ω)向左右平移 4π/Ts,得图 5-29。由图 5-28(c)可知,H(ω)在 2π/Ts 和-2 π/Ts 两个频率的两边是互补对称的,所以在(-2π/Ts,2π/Ts)范围内将平移后的频率特性图 相加,结果为常数 1,由于 n=− H(ω+nωs)具有周期性,故在整个频率轴上进行平移、相加

处理后也为常数1,所以此系统无码间串扰。 图5-29例5-7图2 (d)将H(u)向左右平移4/T.的整数倍得图5-30。显然不能满足奈奎斯特准则 川+y 图5-30例5-7图3 小结根据(©)的分析结论可知,当给定系统的频率特性H()时,可以找出H(f)的互补 对称频率,最大无码间串扰码速率等于这个互补对称频率的两倍。在(c)中,H()的互补对 称顷率为1/T,故最大码速率为2/T。 在()中,H(f)的互补对称频率为1/(2T),故最大无码间串扰的码速率为1/T,实际码速率 为2/ 码间串扰。 常将这个互补对称频*称为等效矩形带宽W。由()求等效矩形带宽黑,确定无码间串 扰的最大码速率R。ax=2W,再与实际码速率R比较,若Rmx/R为正整数,则无码间串 扰,否则有码间串扰。这是根据系统频率特性()分析码间串扰特性的一个简便方法。 【例5-8】为了传送码元速率R=103B阳的数字基带信号,试问系统采用图5-31中所 画的哪一种传输特性较好?并简要说明其理由。 H(御, -4×10x-2×103x-10x010*x2×10r4×10x 图5-31别5-8图 思路可从码间串扰性能、频带利用率、时域收敛速率以及可实现性等四个方面进行比较,从 而确定选择哪一种传输特性, 解(1)码间串扰性能 (a)因等效矩形带宽W=103Hz,故Bmax=2X103Bd,RDax=2Ra,无码间串扰. (亿b)Rmax=2X103Bd,无码间串扰。 (C)因等效矩形带宽W=500z,故Rmx=l03BdR,无码间串扰 (②)频带利用率 (a)、(⑥)、(c)三种传输特性所占用的信道带宽分别为2×103z、103z、10z,所 以它们的频带利用率分别为0.5Bd/Hz、1Bd/Hz、1Bd/Hz。 (3)时域收敛速率
7 处理后也为常数 1,所以此系统无码间串扰。 图 5-29 例 5-7 图 2 (d) 将 H(ω)向左右平移 4π/Ts 的整数倍得图 5-30。显然不能满足奈奎斯特准则。 图 5-30 例 5-7 图 3 小结 根据(c)的分析结论可知,当给定系统的频率特性 H(f)时,可以找出 H(f)的互补 对称频率,最大无码间串扰码速率等于这个互补对称频率的两倍。在(c)中,H(f)的互补对 称频率为 1/Ts,故最大码速率为 2/Ts。 在(d)中,H(f)的互补对称频率为 1/(2Ts),故最大无码间串扰的码速率为 1/Ts,实际码速率 为 2/Ts,故有码间串扰。 常将这个互补对称频率称为等效矩形带宽 W。由 H(f)求等效矩形带宽 W,确定无码间串 扰的最大码速率 RB max=2W,再与实际码速率 RB 比较,若 RB max/RB 为正整数,则无码间串 扰,否则有码间串扰。这是根据系统频率特性 H(f)分析码间串扰特性的一个简便方法。 【例 5-8】 为了传送码元速率 RB=103 Bd 的数字基带信号,试问系统采用图 5-31 中所 画的哪一种传输特性较好?并简要说明其理由。 图 5-31 例 5-8 图 思路可从码间串扰性能、频带利用率、时域收敛速率以及可实现性等四个方面进行比较,从 而确定选择哪一种传输特性。 解 (1) 码间串扰性能 (a) 因等效矩形带宽 W=103 Hz,故 RB max=2×103 Bd,RB max=2RB,无码间串扰。 (b) RB max=2×103 Bd,无码间串扰。 (c) 因等效矩形带宽 W=500 Hz,故 RB max=103 Bd=RB,无码间串扰。 (2) 频带利用率 (a)、(b)、(c)三种传输特性所占用的信道带宽分别为 2×103 Hz、103 Hz、103 Hz,所 以它们的频带利用率分别为 0.5 Bd/Hz、1 Bd/Hz、1 Bd/Hz。 (3) 时域收敛速率