DFS的一些性质 ▣时域移位 (n+m)←s→(k)Wm ▣频域移位 (调制特性)W()←Ds→(k+) ▣对偶性 (n)KDs→(K)〉 (n)←s→N(-k) 口周期卷积和(条件?) N-I jm)=∑,(m)e,(n-m) ()=文(k)(k) =0 ≠x1(m)*x2(n) (n)=元(n)e,(m)〉 =2求x,-) ≠文(K)*文(K)
时域移位 DFS的一些性质 DFS ( ) () mk N xn m X kW 频域移位(调制特性) DFS () ( ) nl W xn Xk l N 对偶性 DFS x() () n Xk DFS X() ( ) n Nx k 周期卷积和(条件?) 1 2 Yk X k X k () () () 1 1 2 0 1 2 () ( ( )* ) ) ( ( ) N m y x n n xn x mx n m 1 2 y () () () n x nx n 0 2 1 1 1 2 1 ( ) () ( ) ( )* ( ) N l Yk X lX k l k Xk N X

离散傅里叶变换及快速算法 主要内容 周期序列的DFS及性质 ◆>■离散傅里叶变换(DFT)及性质 DFT的快速算法(FFT) aDFT/FFT的应用
离散傅里叶变换及快速算法 主要内容 周期序列的DFS及性质 离散傅里叶变换(DFT)及性质 DFT的快速算法(FFT) DFT/FFT的应用

离散傅里叶变换及性质 如果信号不是周期的,有没有办法利用计算机获 取/存储其时频域特征? 条件1:时域离散,有限长/周期 条件2:频域离散,有限长/周期 √ 时域有限,频域无限! 怎么办? 1构造周期信号 一信号周期延拓 (n)=∑x(n+rW)=x(n)N r=-00 有限长序列是周期信号 x(n)=(n)R (n) 的主值序列
离散傅里叶变换及性质 如果信号不是周期的,有没有办法利用计算机获 取/存储其时频域特征? 条件1:时域离散,有限长/周期 条件2:频域离散,有限长/周期 时域有限,频域无限! 怎么办? 构造周期信号 —— 信号周期延拓 () ( ) r x n x n rN () () () N x n xnR n 有限长序列是周期信号 的主值序列 (( )) N x n

离散傅里叶变换(DFT) ▣ DFT的定义 X)=兑mr 0≤k≤N-1 =0 注意N的含义 m=大2Xkwg40≤n≤N-1 周期! N k=0 ▣DFT与DFS的关系 x(n)=(n)R (n) DFT是DFS的主值序列 X(k)=x(k)Rv(k) (n)=x(n)) √DFS是DFT的周期延拓 ()=X(k)
1 0 1 0 ( ) ( ) 0 1 1 ( ) ( ) 0 1 N nk N n N nk N k X k x nW k N xn X kW n N N 离散傅里叶变换(DFT) 注意N的含义 DFT的定义 DFT与DFS的关系 DFT是DFS的主值序列 () () () () () () NN xn xnR n Xk XkR k DFS是DFT的周期延拓 NN xn x n Xk X k 周期!
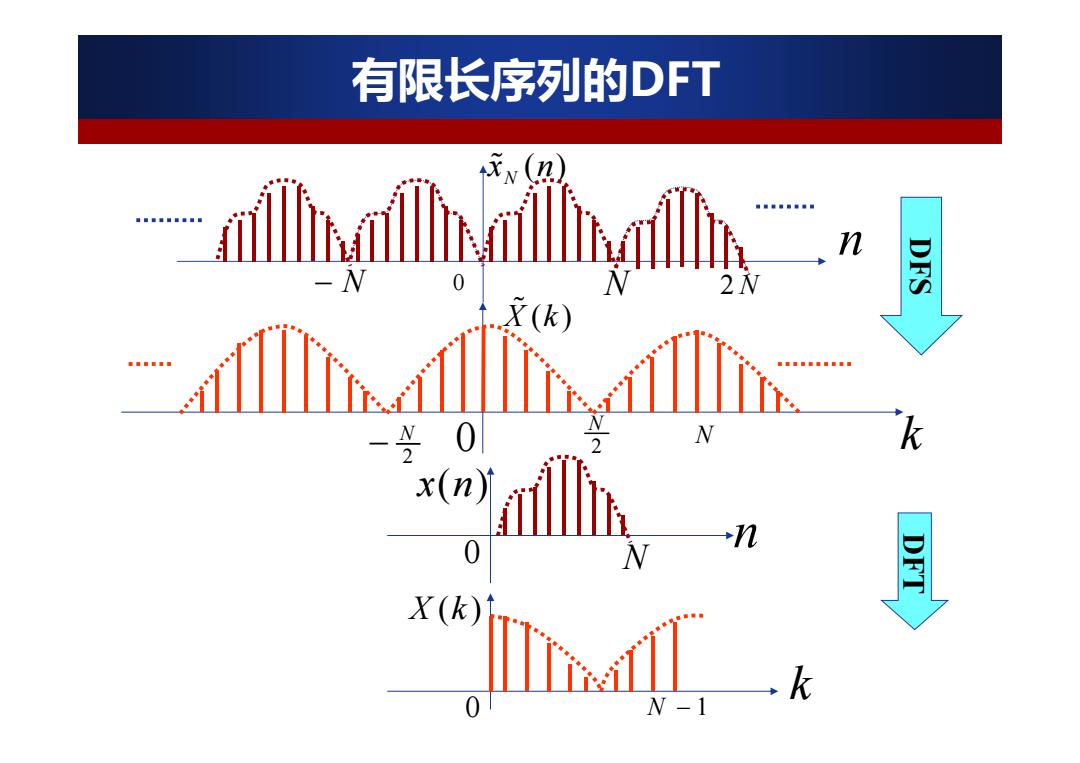
有限长序列的DFT n DFS X(k) ■■■■■ ■■■■■重■■■ N k x(n N n X(k) k 0 W-1
( ) N x n n N 0 N 2 N X ( ) k 0 2N N k 0 N n x(n) 0 N 1 k X (k ) DFS DFT 2N 有限长序列的DFT