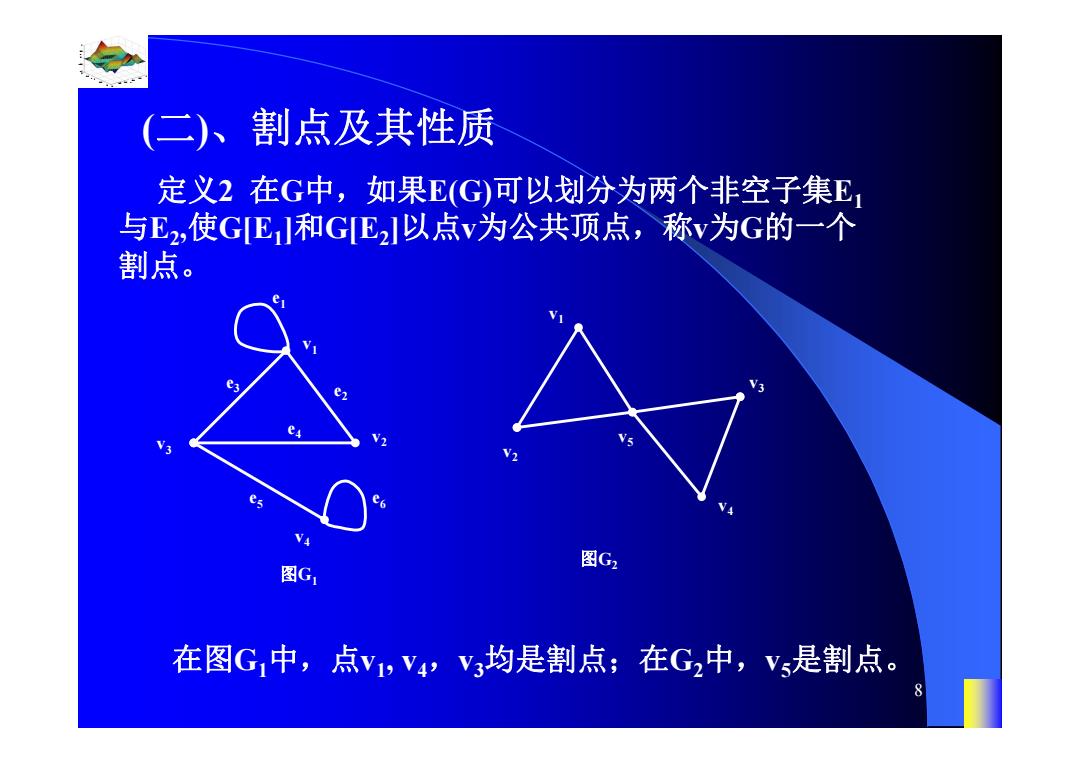
(二)、割点及其性质 定义2在G中,如果E(G)可以划分为两个非空子集E, 与E2,使GE]和GE以点v为公共顶点,称v为G的一个 割点。 图G2 图G, 在图G,中,点v1,V4V均是割点;在G2中,Vs是割点。 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 (二)、割点及其性质 定义2 在G中,如果E(G)可以划分为两个非空子集E1 与E2,使G[E1]和G[E2]以点v为公共顶点,称v为G的一个 割点。 v1 v v2 3 v4 e3 e1 e2 e4 e5 e6 图G1 v1 v3 v2 v4 v5 图G2 在图G1中,点v1, v4,v3均是割点;在G2中,v5是割点

定理2G无环且非平凡,则v是G的割点,当且仅当 @(G-v)>@(G) 证明:“必要性” 设v是G的割点。则E(G可划分为两个非空边子集E, 与E2,使GE,l,GE2恰好以v为公共点。 由于G没有环,所以,GE,GE分别至少包含异于v的 G的点,这样,G-v的分支数比G的分支数至少多1,所以: @(G-v)>@(G)
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 定理2 G无环且非平凡,则v是G的割点,当且仅当 ( ) () Gv G 证明:“必要性” 设v是G的割点。则E(G)可划分为两个非空边子集E1 与E2,使G[E1],G[E2]恰好以v为公共点。 由于G没有环,所以,G[E1],G[E2]分别至少包含异于v的 G的点,这样,G-v的分支数比G的分支数至少多1,所以: ( ) () Gv G