中国地质大学（武汉）：《数字信号处理》课程教学资源（课件讲稿）第六章 IIR数字滤波器的设计方法

一阶全通系统： jlm 小2号 a为实数 1/a 0<la<1 0 Rel] 极点：z=a零点：z=1/a 图6-3a为实数，0<a<1时，一阶全通系统的零点-极， Ho(=)=a' a为复数 jIm(l 1-az-' 0<a<1 1/a* 极点：z=a零点：z=1/a 1 0 Rel] 零极点以单位圆为镜像对称

一阶全通系统： 1 1 ( ) 1 ap z a H z a az      为实数 0 1   a 极点： z a  零点： z a 1/ 零极点以单位圆为镜像对称 极点： z a  1 * 1 ( ) 1 ap z a H z a az      为复数 0 1   a * 零点： z a 1/

◆实系数二阶全通系统 1-az11-a*z a<1 极点：z=a,a jIm(l 零点：z=1/a,1/a 1/a 两个零点（极点）共轭对称 零点与极点以单位圆为镜像对称 图6-5二阶全通系统的零点-极点位置

实系数二阶全通系统 1 * 1 1 1 ( ) 1 1 * ap z a z a H z az a z           a 1 两个零点（极点）共轭对称 * 极点： z a a  ， * 零点： z a a 1/ ，1/ 零点与极点以单位圆为镜像对称

◆N阶数字全通滤波器 eia k=1 =±+dx++dg0w-)+zN 1+dz+.+dy-+dyzN =±*D D(a) 极点：D(z)的根 2p=retio r<1 零点：D(z)的根 5，=1e<1

 N 阶数字全通滤波器 1 * 1 1 ( ) 1 N k k k z a H z a z        1 ( 1) 1 1 1 ( 1) 1 1 ... 1 ... N N N N N N N N d d z d z z d z d z d z                     1 ( ) ( ) N z D z D z     极点： D z( ) 的根 1 j p z re r     零点：D z( ) 1 的根 1 1 j o z e r r    

◆全通系统的应用 1)任一因果稳定系统H()都可以表示成全通系统 Hape)和最小相位系统Hmin(e)的级联 H(z)=Hmm(e)·Hm(2） 令：H(a)=H,(2z1-2o(z1-) 其中：H(@)为最小相位延时系统， 1/zo,1/20o<1为单位圆外的一对共轭零点

全通系统的应用 min ( ) ( ) ( ) H z H z H z   ap 1）任一因果稳定系统H(z)都可以表示成全通系统 Hap(z)和最小相位系统Hmin(z)的级联 1 1 * 1 0 0 H z H z z z z z ( ) ( )( )( )   令：    其中：H1 (z)为最小相位延时系统， 为单位圆外的一对共轭零点 * 0 0 0 1/ 1 z z z ，1/ ， 

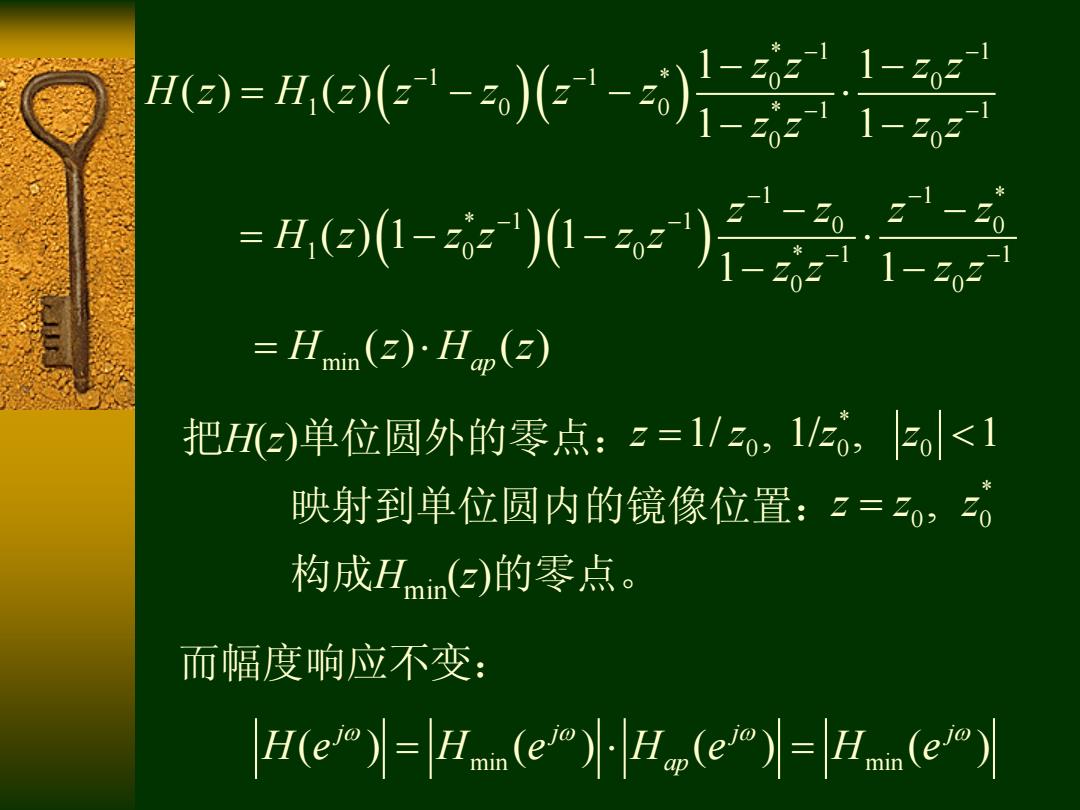
-ae- 6-中语 =Hmin(z)Hp(e） 把He)单位圆外的零点：2=1/2o,12,o<1 映射到单位圆内的镜像位置：2=2,0 构成Hmin(g)的零点。 而幅度响应不变： H()=H(e)H(=H(e)

   * 1 1 1 1 * 0 0 1 0 0 * 1 1 0 0 1 1 ( ) ( ) 1 1 z z z z H z H z z z z z z z z z                  1 1 * * 1 1 0 0 1 0 0 * 1 1 0 0 ( ) 1 1 1 1 z z z z H z z z z z z z z z               min ( ) ( )   H z H z ap 把H(z)单位圆外的零点： 映射到单位圆内的镜像位置： 构成Hmin(z)的零点。 * 0 0 0 z z z z   1/ , 1/ , 1* 0 0 z z z  , 而幅度响应不变： min min ( ) ( ) ( ) ( ) j j j j H e H e H e H e ap       