
色谱分析的依据: ()色谱峰的位置(即保留时间或保留体积)决定于物质的性 质,是色谱定性的依据; (2)色谱峰的高度或面积是组分浓度或含量的量度,是色 谱定量的依据; (3)色谱峰的位置与其宽度,可以对色谱柱分离的情况进 行评价。 (4)样品中所含组分数(峰个数)
色谱分析的依据: (1)色谱峰的位置(即保留时间或保留体积)决定于物质的性 质,是色谱定性的依据; (2)色谱峰的高度或面积是组分浓度或含量的量度,是色 谱定量的依据; (3)色谱峰的位置与其宽度,可以对色谱柱分离的情况进 行评价。 (4)样品中所含组分数(峰个数)

三)塔板理论 1. 塔板理论假定为了研究谱峰的形状,建立起一种半经验式的 理论一塔板理论,用于描述物质在两相间的分配状况和评价 柱的效能。塔板理论是把柱子假想成由许多塔板组成,在每个 理论塔板里,组分在气液相间达成一次平衡,经过多次分配平 衡后,使组分彼此分离。为简花起见,塔板理论有如下假设: (1)在每块板上气液平衡是瞬间建立的。 (2)载气是脉冲式进入色谱柱进行冲洗的,每次恰好为一个板体 积。 (3)所有组分开始都集中在第零块塔板上,且不考虑纵向扩散。 (4)在所有塔板上,分配系数是常数,也即和组分的量无关
三)塔板理论 1.塔板理论假定 为了研究谱峰的形状,建立起一种半经验式的 理论——塔板理论,用于描述物质在两相间的分配状况和评价 柱的效能。塔板理论是把柱子假想成由许多塔板组成,在每个 理论塔板里,组分在气液相间达成一次平衡,经过多次分配平 衡后,使组分彼此分离。为简化起见,塔板理论有如下假设: (1)在每块板上气液平衡是瞬间建立的。 (2)载气是脉冲式进入色谱柱进行冲洗的,每次恰好为一个板体 积。 (3)所有组分开始都集中在第零块塔板上,且不考虑纵向扩散。 (4)在所有塔板上,分配系数是常数,也即和组分的量无关

2.理论塔板数 在假定理想情况下,可以认为进人柱子内的样品成分在载 气中是呈“正态分布”的,因而,在记录纸上出现的色谱峰应 为高斯(Guss)曲线。所以色谱峰常用与高斯曲线宽度相关的某 一标准偏差σ表示。图4一3表明在不同高度位置上峰宽度与σ的 关系
2.理论塔板数 在假定理想情况下,可以认为进人柱子内的样品成分在载 气中是呈“正态分布”的,因而,在记录纸上出现的色谱峰应 为高斯(Gauss)曲线。所以色谱峰常用与高斯曲线宽度相关的某 一标准偏差σ表示。图4—3表明在不同高度位置上峰宽度与σ的 关系
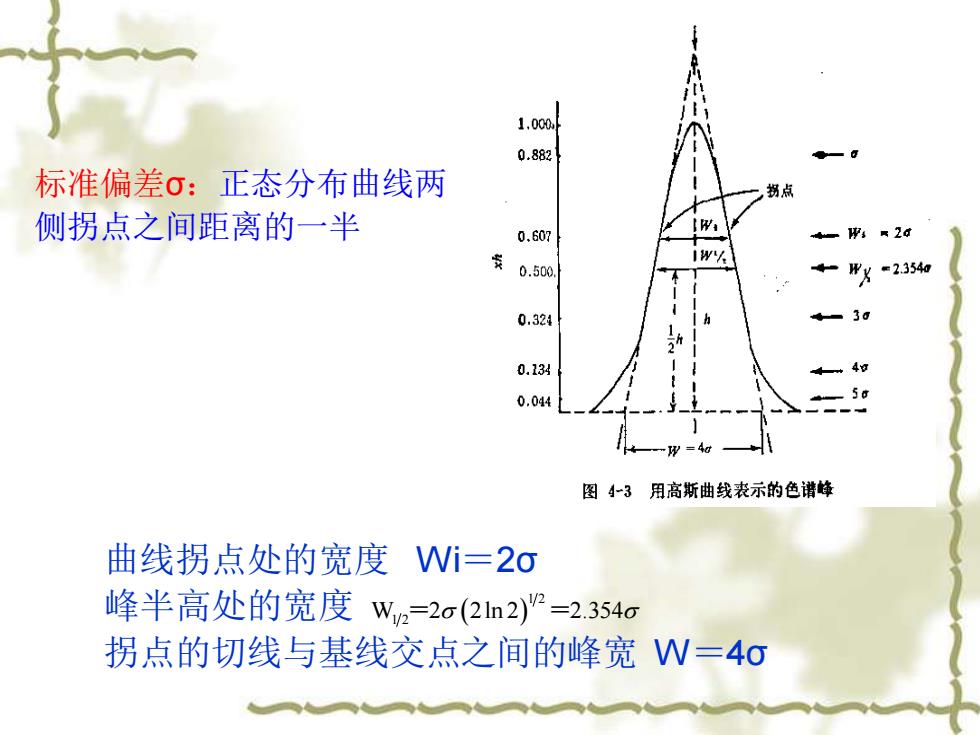
1.000, 0.882 标准偏差σ:正态分布曲线两 拐点 侧拐点之间距离的一半 0.607 一:2d 1W/A 0.500 Wg=2354和 0.324 3g 0.134 4过 0.044 -5 图43用高斯曲线表示的色谱峰 曲线拐点处的宽度Wi=2o 峰半高处的宽度w,e=2o(2In2)=2.354o 拐点的切线与基线交点之间的峰宽W=4σ
标准偏差σ:正态分布曲线两 侧拐点之间距离的一半 曲线拐点处的宽度 Wi=2σ 峰半高处的宽度 拐点的切线与基线交点之间的峰宽 W=4σ ( ) 1 2 W 2 2ln 2 2.354 1 2 = =

作为塔板理论的结论,理论塔板 数n可用下式中: n=16(tRW)2 由于W=40,所以,n=tR2/02 理论塔板高H=L(柱长)n, 理论踏板数n>50(n=L/D时,可得到基本对称的峰型曲线 有效塔板高
作为塔板理论的结论,理论塔板 数n可用下式中: n=16(tR/W)2 由于W=4σ,所以,n= tR 2 / σ2 理论塔板高H=L(柱长)/n, 理论踏板数n>50(n=L/H)时,可得到基本对称的峰型曲线 有效塔板高