例8-320a号工字钢悬臂梁承受均布荷载和集中力F=qa2如图。已知钢的许用弯曲正应力[]=160MPa,a=1 m。 试求梁的许可荷载集度[g]H40°解:作计算简图,将自由端截面B上的集中力沿两主轴分解为F,=Fcos40°=0.383qaF = F sin 40° =0.321qa0.4440321g在xoz主轴平面内的M图(N.m)R弯矩图(v轴为中性轴)0.617在xoy主轴平面内的M图(N.m)弯矩图(z轴为中性轴)0.456qa2 0.383qa2
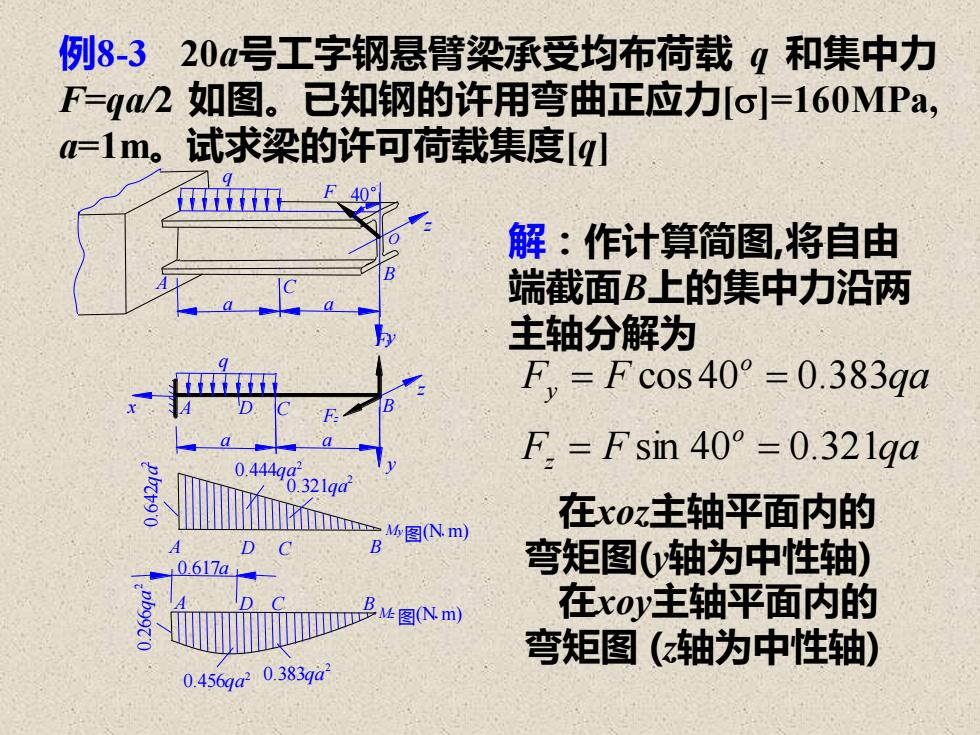
例8-3 20a号工字钢悬臂梁承受均布荷载 q 和集中力 F=qa/2 如图。已知钢的许用弯曲正应力[]=160MPa, a=1m。试求梁的许可荷载集度[q] 解:作计算简图,将自由 端截面B上的集中力沿两 主轴分解为 F F qa F F qa o z o y sin 40 0.321 cos 40 0.383 = = = = 在xoz主轴平面内的 弯矩图(y轴为中性轴) 在xoy主轴平面内的 弯矩图 (z轴为中性轴) y q z a a F 40° O C B A Fy z q a a A D C B Fz y x 0.642qa 0.444qa 0.321qa 2 2 2 A D C B My图(N m) 0.617a A D C B Mz 图 0.456qa 0.383qa 0.266qa 2 2 2 (N m)

危险截面:由弯矩图,可确定B、D两截面为危险截面B、D截面在xoz、xoy平面的弯曲截面系数可查表得W. =237x10-°m3,W,=31.5x10-m按叠加法,在xoz主轴平面内、xoy主轴平面内的弯曲正应力,在x方向叠加MyAM=(21.5×10′ml)截面A:(αmax)AW,W.MyDM.D=(16.02×10′m2)q截面B:(omax)BW,W
危险截面:由弯矩图 ,可确定B、D两截面为危险截面 按叠加法,在xoz主轴平面内、 xoy主轴平面内的弯 曲正应力,在x方向叠加 q W M W M A z z A y yA A 截面 : ( ) (21.5 10 m ) 3 1 max − = + = q W M W M B z z D y yD B : ( ) (16.02 10 m ) 3 1 max − 截面 = + = B、D截面在xoz、 xoy平面的弯曲截面系数, 可查表得 6 3 6 3 237 10 m , 31.5 10 m − − Wz = Wy =

可见,梁的危险点在截面A的棱角处。危险点处是单轴应力状态,强度条件为0 max ≤[o]即(omx)^=(21.5×103m-)q≤160×10°Pa解得[g] = 7.44 ×10' N/m = 7.44kN/m
可见,梁的危险点在截面A的棱角处。危险点处是 单轴应力状态,强度条件为 [ ] max 即 ( ) (21.5 10 m ) 160 10 Pa 3 1 6 max = − A q 解得 [ ] 7.44 10 N/m 7.44kN/m 3 q = =

88-3拉伸(压缩)与弯曲包括:轴向拉伸(压缩)和弯曲偏心拉(压),截面核心1.横向力与轴向力共同作用对于EI较大的杆,横向力引起的挠度与横截面的尺寸相比很小,因此,由轴向力引起的弯矩可以略去不计。可分别计算由横向力和轴向力引起的杆横截面上的正应力,按叠加原理求其代数和,即得在拉伸(压缩)和弯曲组合变形下,杆横截面上的正应力
§8-3 拉伸(压缩)与弯曲 包括: 轴向拉伸(压缩)和弯曲 偏心拉(压),截面核心 1. 横向力与轴向力共同作用 对于EI较大的杆,横向力引起的挠度与横截面的 尺寸相比很小,因此,由轴向力引起的弯矩可以略 去不计。 可分别计算由横向力和轴向力引起的杆横截面上 的正应力,按叠加原理求其代数和,即得在拉伸 (压缩)和弯曲组合变形下,杆横截面上的正应力

北一上图示由两根槽钢组成杆件的计算图在其纵对称面内有横向力F和轴向拉力F共同作用,以此说明杆在拉伸与弯曲组合变形时的强度计算
上图示由两根槽钢组成杆件的计算图,在其纵 对称面内有横向力F和轴向拉力Ft共同作用,以 此说明杆在拉伸与弯曲组合变形时的强度计算。 Ft Ft F 2 h h 2 x y z