
危险点:m-m截面上角点B有最大拉应力,D有最大压应力;E、F点的正应力为零,EF线即是中性轴。可见B、D点就是危险点离中性轴最远强度条件:B、D角点处的切应力为零,按单向应力状态来建立强度条件。设材料的抗拉和抗压强度相同,则斜弯曲时的强度条件为Omax ≤[o]中性轴:正应力为零处,即求得中性轴方程M.M1V=011
危险点:m-m截面上 角点 B 有最大拉应力,D 有最大压应力; E、F点的正应力为零,EF线即是中性轴。 可见B、D点就是危险点,离中性轴最远 强度条件:B、D角点处的切应力为零,按单向应力 状态来建立强度条件。设材料的抗拉和抗压强度相 同,则斜弯曲时的强度条件为 [ ] max 中性轴:正应力为零处,即求得中性轴方程 = − y = 0 I M z I M z z y y

上式可见,中性轴是一条通过横截面形心的直线,E、F点的正应力为零福EF线即是中性轴。其与v轴的夹角为tano--M-tangy M, I I.1是横截面上合成弯矩M矢量与y轴间的夹角。M=M,+M?一般,截面I,,,即叶β,因而中性轴与合成弯矩M所在的平面并不相互垂直。所以曲线将不在合成弯矩所在的平面内,即是斜弯曲。对圆形、正方形等I=I,的截面,得=β,即是平面弯曲
上式可见,中性轴是一条通过横截面 形心的直线, E、F点的正应力为零, EF线即是中性轴。其与y轴的夹角为 tan tan 0 0 z y z y y z I I I I M M y z = = = 是横截面上合成弯矩 M 矢 量与 y 轴间的夹角。 2 2 M = M y + Mz 一般,截面IyIz,即,因而中性轴与合成弯矩 M所在的平面并不相互垂直。所以挠曲线将不在合 成弯矩所在的平面内,即是斜弯曲。 对圆形、正方形等Iy =Iz的截面,得= ,即是平 面弯曲 O z y
例8-1图示悬臂梁,承受载荷F与F作用,已知F,=800N,F,=1.6kN,[-1m,许用应力[o|=160MPa。试分别按下列要求确定截面尺寸:(1)截面为矩形h=2b;(2)截面为圆形。3d福h解:(1)矩形截面:F,21F,1800×21600×1=[q] 即=160×106Tmax463hb?bh?2636666b = 35.6 mm,h = 2b = 71.2 mm
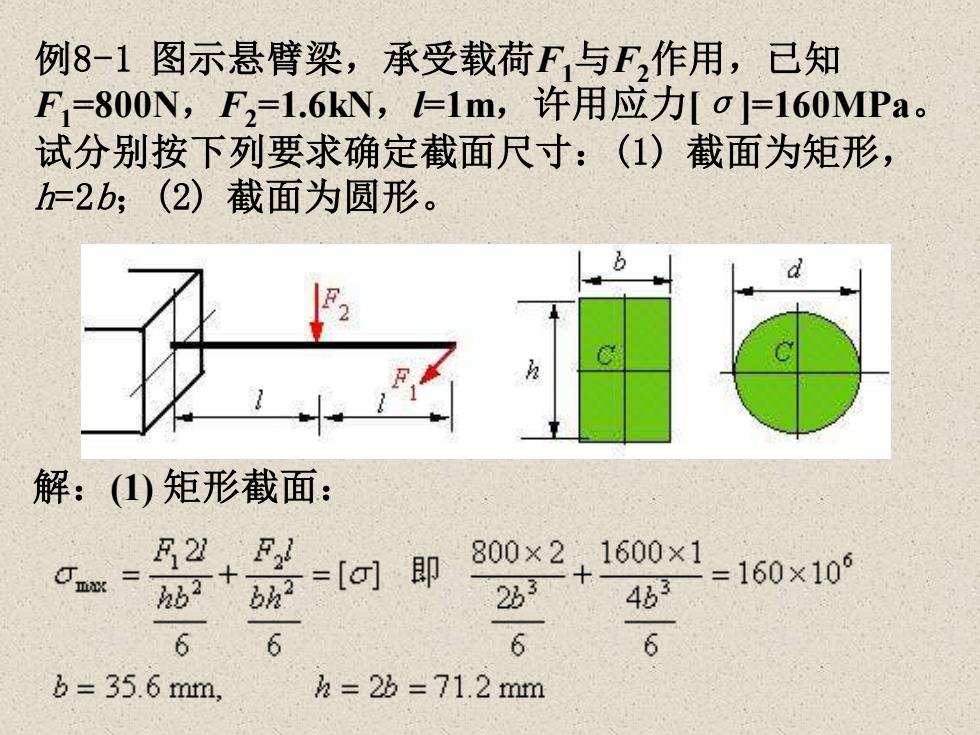
例8-1 图示悬臂梁,承受载荷F1与F2作用,已知 F1=800N,F2=1.6kN,l=1m,许用应力[σ]=160MPa。 试分别按下列要求确定截面尺寸:(1) 截面为矩形, h=2b;(2) 截面为圆形。 解:(1) 矩形截面:

2、圆截面(2)+(F1)3(800×2)+(1600×1)[g] 即160×106Cmand3元d33232d = 52.4 mm
2、圆截面

例8-2图示简支梁。工字钢型号为No.32a,F=60kN,[o]-170MPa,β=5。试校核梁的强度。解:(1)F,=59.77kN, F, =5.23kN(2)Mmx =59.77kN.m, Mvmx =5.23kN.mm(3) W, =692.2cm2,W,= 70.758cmMymax59.77×1065.23×106M.(4) 0)zmaxmax692.2×10370.758×103W.W,= 86.35 + 73.91 = 160.3MPa<[α]
例8-2 图示简支梁。工字钢型号为No.32a,F=60kN, [σ]=170MPa,φ=5o。试校核梁的强度。 F 2m 2m 解:(1) Fy = 59.77k N, Fz = 5.23k N (2) Mzmax = 59.77k N.m, M ymax = 5.23k N.m (3) 3 3 Wz = 692.2cm , Wy = 70.758cm (4) 86.35 73.91 160.3 [ ] 70.758 10 5.23 10 692.2 10 59.77 10 3 6 3 6 max max max = + = + = + = MPa W M W M y y z z