
证明真空中高斯定理的微分形式:利用散度定理:$E-ds =[(V.E)·dV:&0VS[(V.E-P)·dV = 0即0p则V.E82025-6-1116
2025-6-11 16 Ø 真空中高斯定理的微分形式: 利用散度定理: S V V V E ds E dV dq dV 0 0 1 1 ( ) ( ) 0 0 V E dV 即 则 0 E 证明
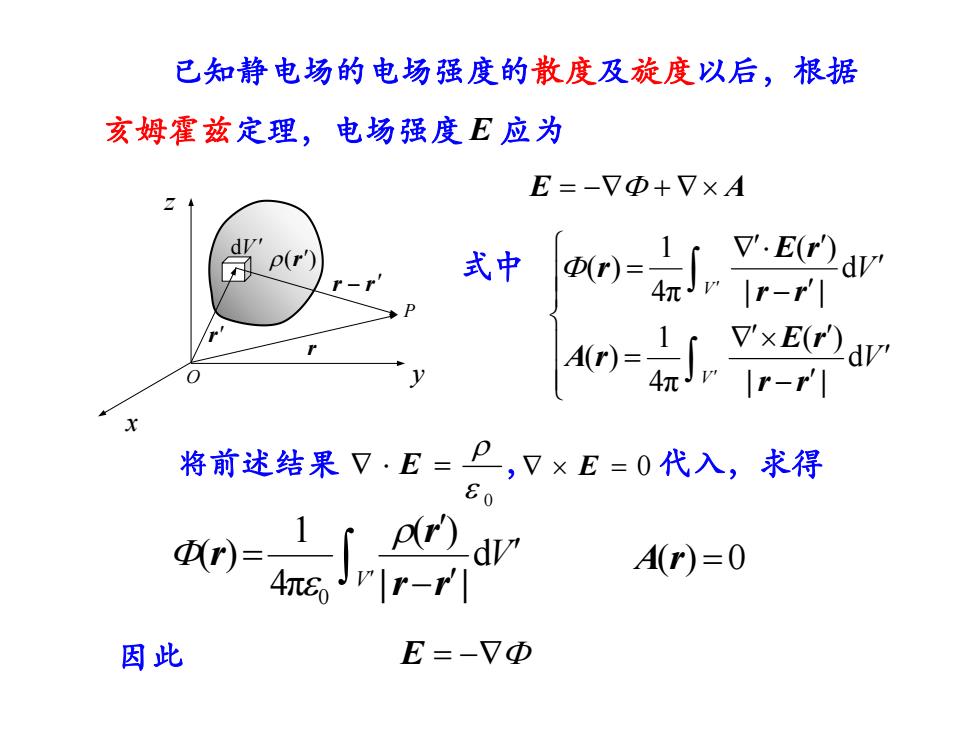
已知静电场的电场强度的散度及旋度以后,根据亥姆霍兹定理,电场强度E应为E=-VΦ+V×AV'.E(r)pr式中Φ(r)=l4元[r-r']V'xE(r)A(r)aly[r-r']将前述结果√.EV×E=0代入,求得8p(r)dVd(r)A(r)=04元E=-VΦ因此
已知静电场的电场强度的散度及旋度以后,根据 亥姆霍兹定理,电场强度 E 应为 E A V V V V d ( ) 4π 1 ( ) d ( ) 4π 1 ( ) |r r | E r A r |r r | E r 式中 r x P z y r O dV (r) r r r V V 0 d ( ) 4π 1 ( ) |r r | r r A(r) 0 因此 E 将前述结果 , 代入,求得 0 E E 0

E=-V@因此标量函数Φ称为电位。因此,上式表明真空中静电场在某点的电场强度等于该点电位梯度的负值。按照国家标准,电位以小写希腊字母β表示,上式应写为E=-Vβ将电位表达式代入,求得电场强度与电荷密度的关系为p(r(r-r'E(r)= (4元8这里利用
标量函数 称为电位。因此,上式表明真空中静 电场在某点的电场强度等于该点电位梯度的负值。 E 按照国家标准,电位以小写希腊字母 表示,上 式应写为 将电位表达式代入,求得电场强度与电荷密度的 关系为 V V d 4π ( )( ) ( ) 3 0 r r r r r E r 因此 E 3 1 r r r r r r 这里利用

若电荷分布在一个有限的表面上,或者分布在一个有限的线段内,那么可以获知此时电位及电场强度与电荷的面密度s及线密度pi的关系分别为Pips((r)10DC4元84元8(rr-ro.(r0rE(rASE(r):[r-r'p4元84元r-r'由上可见,无论电荷如何分布,电位及电场强度均与电荷量一次方成正比,因此可以利用叠加原理计算分布电荷产生的电位及电场强度
若电荷分布在一个有限的表面上,或者分布在一 个有限的线段内,那么可以获知此时电位及电场强度 与电荷的面密度 S 及线密度 l 的关系分别为 0 1 ( ) ( ) d 4π | S S S r r r r | 3 0 1 ( )( ) ( ) d 4π | S S S r r r E r r r | l l l 0 d ( ) 4π 1 ( ) |r r | r r l l l 3 0 d | ( )( ) 4π 1 ( ) r r | r r r E r 由上可见,无论电荷如何分布,电位及电场强度 均与电荷量一次方成正比,因此可以利用叠加原理计 算分布电荷产生的电位及电场强度。 S S' l l

静电场特性的进一步认识①高斯定律中的电量应理解为封闭面S所包围的全部正负电荷的总和。2)静电场的电场线不可能相交,而且也不可能闭合。③静电场中,任意两点之间电场强度E的线积分与路径无关。静电场和重力场一样,它是一种保守场。4已知电荷分布的情况下,可以利用高斯定理计算电场强度,或者可以通过电位求出电场强度,或者直接根据电荷分布计算电场强度等3种计算静电场的方法。5)电位及电场强度符合叠加原理
① 高斯定律中的电量 q 应理解为封闭面 S 所包围的全部 正负电荷的总和。 静电场特性的进一步认识 ② 静电场的电场线不可能相交 ,而且也不可能闭合。 ③ 静电场中,任意两点之间电场强度 E 的线积分与路径 无关。静电场和重力场一样,它是一种保守场。 ④ 已知电荷分布的情况下,可以利用高斯定理计算电场 强度,或者可以通过电位求出电场强度,或者直接根据电 荷分布计算电场强度等 3 种计算静电场的方法。 ⑤ 电位及电场强度符合叠加原理